From high school trigonometry you remember that the sine of an
angle of a right triangle is defined as the ratio of the opposite
side over the hypotenuse. From the calculus, you will recall that
the sine is a differentiable function $ \sin(\theta) $
from the reals to the interval
$ \[-1,1 $] equal to the x-coordinate of a point on the
unit circle that has travelled a total arclength of $ \theta $
units from $ (1,0) $. Recall that a line segment cutting
across a circle is called a secant, and sometimes it is also
called a chord of the circle.
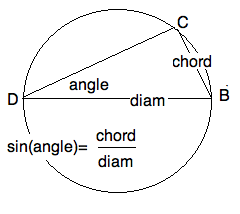
|
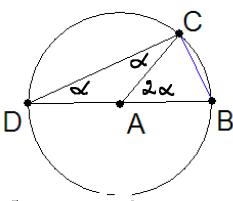
The sine of an angle. |
The Greeks called the ratio of a secant $ BC $
to the diameter $ DB $ of a circle the chord of the
peripheral angle $ \angle BDC $ subtending the secant.
As we shall see, this is also the sine of the angle. The word
"chord" was translated into Arabic "jiba" ( from Sanscrit "jya" or
"bow string")
by the scholars in Baghdad who preserved Greek geometry during
the Dark Ages. When Gherardo of Cremona (ca 1150) translated
geometry from Arabic to Latin, he mistook the word for "jaib"
or "bosom, fold in a garment, curve" in Latin, "sinus".
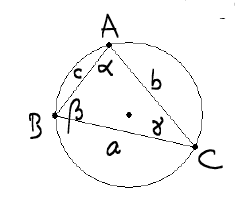
|
Standard Labels |
This definition yields an easy proof of the
Proof.
From $ \sin \alpha = \frac{a}{d} $ where $ d $ is the
diameter of the circumcircle $ \bigcirc ABC $, we see that
the three ratios each equal the reciprocal of the diameter. Hence they
are equal to each other.
Of course, this proof begs the question: if the angle is transferred
to a different circle, then the ratio of its new subtended secant to the
new diameter is the same as the old. In particular, we would like to know
that given a secant of a circle, every peripheral angle subtending this
this secant has the same sine in the traditional sense.
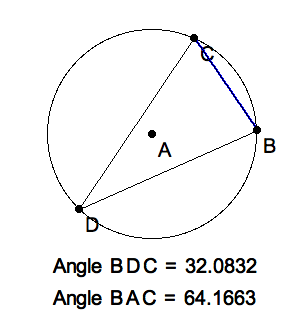
|
Click image to download PAT.seg to explore it in KSEG. |
Comment.
We will prove this theorem in 3 steps. The first depends on an older
theorem on exterior angles of Euclidean triangles. By "older", we mean
it was proved closer to the postulates in Euclid’s Elements. By keeping
track of the age of theorems we avoid circular reasoning.
3.1. Proof of EXT
You should use ruler and compass or KSEG to draw the figure being described
here. We purposely do not include a picture of it so that you can practice
following a description of a figure.
Double the median $ A A' $ to $ E $ beyond the midpoint
$ A' $ of $ BC $, and connect $ E $ to $ B $.
For reference, label a point on $ (AB)$ beyond $ B $, i.e.
so that $ B $ is between $ A $ and $ D $.
Because
$ A A' \cong EA' $ |
$ \angle A A'C \cong \angle EA'B $ |
$ C A' \cong BA' $ |
We have that $ \triangle A A' C \cong \triangle EA'B $.
Therefore $ \angle ACA' \cong \angle EBA' $ and
$ CA || BE $. But then
$ \angle BAC \cong \angle DBE $ and we’re done.
Question 1.
What happens if the triangle is isosceles, with $ |B-A|=|B-C| $?
The the exterior angle is twice (either) of the opposite interior angles.
3.2. Proof of PAT when angle grazes the center
We can imagine the problem to be that of finding a good place to sit
in a loge of in a circular theater.
La Scala and Schakespeare’s Globe Theater had its loges arranged
in a circular wall. By the PAT, every loge occupant saw the stage (a
secant) with the same angle, hence the same apparent width.
Of course, the distortion
could not be avoided, and the queen still sat directly in the royal
loge opposite the stage.
Let $ A $ be the center of the circle, a lie on angle-leg
$ DB $. By the EXT, the peripheral angle is half the central
$ \angle BAC $. Since $ \triangle DCB $ is inscribed
in a semicircle, it is a right triangle, and
$ \sin D = \frac{CB}{diameter}$, justifying the two Greek
definitions of the sine of an angle. It also proves
Corollary.
The length of a secant of a circle is the diameter times the sine
of half the central angle it subtends.
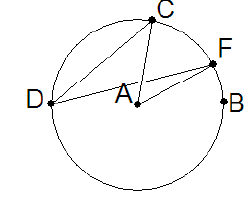
3.3. Proof of PAT when angle sees the center
 |
Click image to download PAT.seg to explore it in KSEG. |
This means, that $ A $ lies inside the angle. Draw the
diameter $ DAE $ and observe that we have two cases of
the first case, one above this diameter, and one below. Thus
$ \angle BDC = \angle BDE + \angle EDC = \frac{1}{2} (\angle BAE + \angle EAC) = \frac{1}{2} \angle BAE $ |
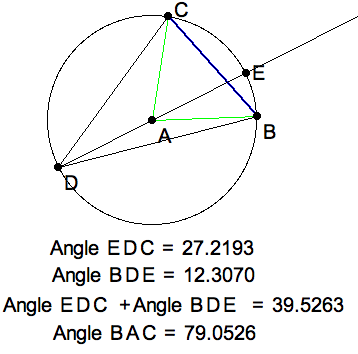
|
Click image to download PATadder.seg which opens in KSEG. |
|
Exercise 1.
Apply a similar argument, with subtraction replacing addition of
periferal and central angles for the last case, that the periferal
angle does not see the center.
So, we have exhaustively proved PAT. You should note that we have used
exclusively Euclidean arguments, very possibly the proof that Euclid
wrote in his Elements.
Question 2.
What happens when the periferal angle dips behind the stage?
Suddenly the central angle becomes greater than a straight angle. That is,
the periferal angle become obtuse. But since the two central angles add
up to $ 2 \pi $, any two periferal angles, one "in front" and
one "behind" the secant "stage", become supplementary. But recall, supplementary
angles have the same sine.
Definition.
The cross ratio, $ CR(A,B,C,D $, of four (distinct) collinear
points, is
$ CR(A,B,C,D) = \frac{A-B}{A-D} \frac{C-D}{C-B} $
Definition.
The cross ratio, $ CR(a,b,c,d) $, of four (distinct) concurrent
lines, is
$ CR(a,b,c,d) = \frac{\sin \angle ab}{\sin \angle ad} \frac{\sin \angle cd}{\sin \angle cb} $
Note the direction in which we measure a segment matters here,
$ \frac{A-B}{A-D} = - \frac{B-A}{A-D} $, and so does the
orientation in which we measure an angle, $ \sin \angle ab = - \sin \angle ba $.
However, for two crossing lines, it doesn’t matter which of the two
angles we use; being supplementary, their sins are the same.
For notational symmetry, we have measured the angles clock-wise. It doesn’t
matter, as long as are consistent. Changing the sign of an angle changes
the sign of its sin, but not the ratio of two angles whose sign was reversed.
See how it would have been better if Gherardo had used the word "chord".
On the other hand, "cochord" might sound worse than "cosine".
4.1. Proof of CRT
First, we abbreviate $ sin AB = \sin \angle APB = \sin \angle ab $ etc.
That would be the angles at $ P $. Second, we abbreviate
$ \sin B = \sin \angle PBA = \sin \angle CBP $ because these
two angles are supplementary, and so have the same sines. Finally, we show
that two numbers are equal by showing that their ratios equals $ 1 $.
$ \frac{CR(A,B,C,D)}{CR(a,b,c,d)}$ |
$ = \frac{ \frac{A-B}{A-D} \frac{C-D}{C-B} }{ \frac{sin AB}{sin AD}\frac{sin CD}{sin CB} } $ |
$ = \frac{ \frac{A-B}{sin AB} \frac{C-D}{sin CD} }{ \frac{A-D}{sin AD}\frac{C-B}{ sin CB} } $ |
$ = \frac{ \frac{P-A}{sin B} \frac{P-C}{sin D} }{ \frac{P-A}{sin D}\frac{P-C}{ sin B} } $ |
$ = \frac{ \frac{P-A}{P-A} \frac{P-C}{P-C} }{ \frac{sin B}{sin D}\frac{sin D}{sin B} } $ |
$ = 1 $. |
The rearrangement of the fractions has to be undertood carefully. Since
everything is happening on the same line, we have replaced the
vector $ A-D $ by its signed length (the direction matters!).
Now we apply the Law of Sines judiciously. Can you find the four triangles
in which we replace ratios? This time we are allowed to replace vectors
by their signed length because all four are concurrent. This is a little
subtle, but has to be said here for completeness.
Comment.
Pretty neat, huh? Mathematicians die for clever arguments like this. The
alternative is a considerable longer. While each step of the un-clever
argument might be easier to see, there are so many of them that you loose
the forest for the trees.
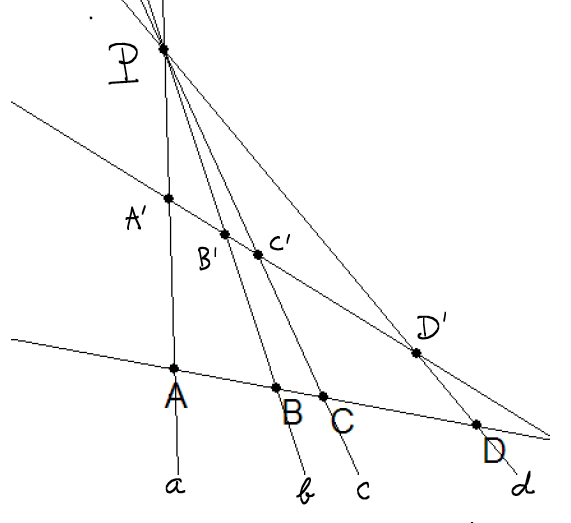
Two sets of four collinear points, $ (ABCD), (A'B'C'D') $ are
said to be in perspective position, if the four lines
$ (A'A) (B'B) (C'C) (D'D) $ are concurrent.
s
4.2. Proof of the PIT
With $ a=(A'A) $ etc, observe that
$ CR(A,B,C,D) = CR(a, b, c, d) = CR (A',B',C',D') $. |
By a ruler we mean a line with a copy of the real numbers marked on
it. Recall from high school, that $ \ell = (AB) $
can be given a ruler by assignin $ A |-> 0 $ and $ B |-> 1 $.
In particular, we can find all multiples and fractions of unity by
ruler and compass. Multiples are easy.
Question 3.
How would you subdivide the segment $ AB $ in 7 equal pieces?
If instead of 7 we wanted some power of 2, then taking repeated halves
would solve our problem. In fact, by just marking fractions with powers
of two in their denominator (think of the inch-system) would work quite
nicely in the real world. Such fractions are also called binary fractions.
We can approximate every real number by a sequence of convergent binary
fractions.
But to get an accurate, and for that matter quicker, answer we can use
a similarity theorem from high school geometry. You’ll need pencil and
paper to follow along.
On another line $ AC $ extend $ AC $ seven times to $ D $. Now $ AC = \frac{1}{7} AD $. Now draw $ BD $ and a line
parallel to $ BD $ through every multiple of $ AC $ on the
helper line. These mark off seven equal pieces on the given segment
$ AB $.
Comment.
The previous construction is actually a case of PIT, if we understand
mutually parallel as concurrent at infinity. Although it is true, we
have not proved PIT for this extended case.
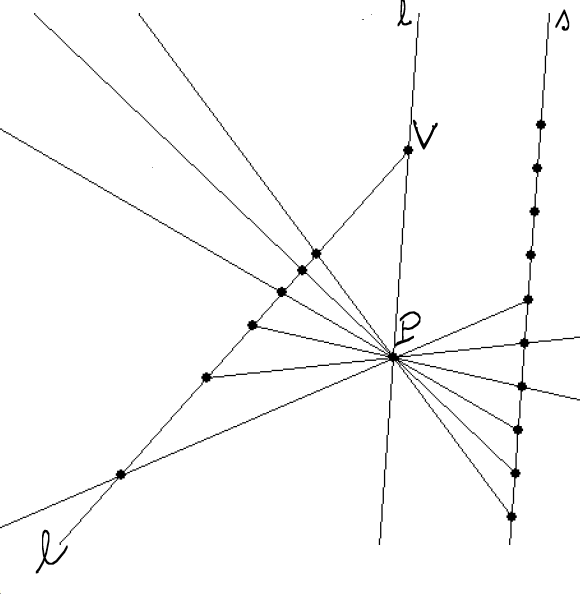
Now, finally, consider a ray in the canvas at $ V $ and two
points, $ Q I $ on the ray. Thus in the Euclidean plane of the
canvas $ (QIV) $. This represents an infinite line in space, but
in perspective. Equally spaced points on the space line would not be
drawn with equally spaced points in perspective. The points have to
get more and more close to each other as they approach the vanishing
point $ V $.
To find these milestones you may choose any convenient point $ P $
in the canvas, but not on the line $ (QI) $. We shall call
$ P $ a lens. Now choose any
other line parallel $ s $ to $ (PV) $ that is convenient
to work with. We shall call $ s $ a scale for the perspective
line $ (VIQ) $.
Now transfer $ Q, I $ to $ s $ by drawing
lines through $ P $. That is
$ Q' = (QP)s \and I' = (IP)s $.
Question 4.
Calculate $ CR(X,Q,I,V) = CR(X',Q',I',V') $ ?
$ \frac{X-Q}{X-V} \frac{I-V}{I-Q} = \frac{X'-Q'}{X'-V'} \frac{I'-V'}{I'-Q'} $
Notice the $ V' $ does not exist. The line $ (PV) $ is
parallel to the scalin line $ s $
and so meets it at $ \infty $. If we identify
$ X' = x, Q' = 0, I' = 1 $ then we should also
let $ V'= \infty $. Then the cross ratio becomse
$ \frac{x-0}{x-\infty}\frac{1-\infty}{1-0} = x $.
This applies a perspective ruler on the perspective line $ (OQV) $.
Therefore, for two points $ X(QV) \and Y(QV) $ we can assign the
perspective distance
$ dist_{QV}(XY) = CR(X,Q,Y,V) = \frac{X'-Q'}{Y'-Q'} $.