Suppose we have a figure inside a rectangular frame, for example a circle
inscribed in a square, and we wish to draw this figure into a perspective
view of the rectangle. In perspective, the rectangle will be a convex
quadrilateral, with two vanishing points. Let the corners of the Euclidean
square be $ ABCD $ and the corresponding corners of the perspective
square in the picture plane be labelled $ A'B'C'D'$. If we draw
the diagonals of both quadrilaterals, then to intersect at $E $ and
$ E' $ respectively, then $ E' $ is the perspective image
of $ E $, the midpoint of the square. To divide the square into
four quarters, we draw lines through $ E $ that are parallel to the
sides of the square. We know how to draw perspective parallels, namely by
connecting $ E' $ with each of the two vanishing points. We can
continue this process indefinitely, and obtain a division of the original
square into grid of 4, 16, 64, 256 … equal squares. And, at the same
time, its perspective image in the picture plane. Such a division
"by halves" is called a binary grid.
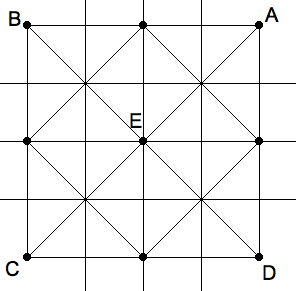
|
Orthogonal four-by-four grid. |
Using a pair of binary grids, one orthographic and the other in perspective,
we can transfer an arbitrary figure in the former to the latter by approximating
the situation in each pair of corresponding squares. You can even imagine
copying from one perspective frame into another, at least approximately.
Duerer’s picture of the artist using Alberti’s Veil is an example of this
technique.
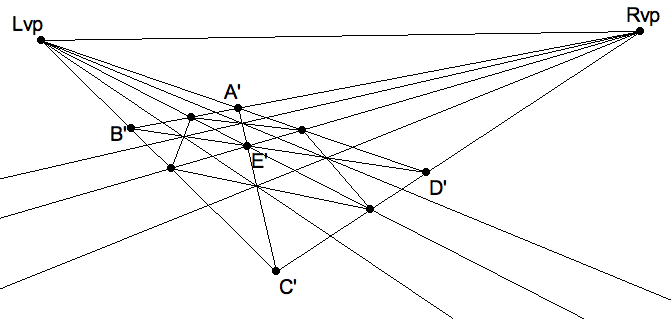
|
Four-by-four grid in perspective. |
Now consider the circle inscribed into a square. Diagonalize once to obtain
the cross of a cartesian coordinate system with origin the center of the
Euclidean square $ ABCD $. Where the axes intersect the sides of the
square are four points on the circles. Subdivide once more to obtain a grid
of 16 squars. The 4 additional lines have equations
$ x= \pm \frac{1}{2}, y = \pm \frac{1}{2} $. Imagine, but do not
draw, two further binary subdivisions, so that lines like
$ y=\frac{7}{8} $ have their perspective counterparts in the
picture plane. By the Pythagorean theorem, the point 8 points
$ ( \pm \frac{1}{2}, \pm \frac{7}{8}),
( \pm \frac{7}{8}, \pm \frac{1}{4}) $ all are very nearly on the unit
circle because
$ \frac{1}{2}^2+\frac{7}{8}^2=\frac{4}{8}^2+\frac{7}{8}^2=\frac{16+49}{64}=\frac{65}{64} ~ 1 $ |
Now, these eight "seven-eighths" points can be located already on the 2nd
grid (the one with 16 squares) with the help of four diagonals of 1 by 4
rectangles. Consider an orthographic rectangle in the proportion 4:1.
The diagonal starting at the upper left corner cuts the first vertical
quarter line at its $ \frac{3}{4} $ point, the second at its
midtpoint etc. Only the first crossing is of interest, because
$ \frac{1}{2}+\frac{3}{4}\frac{1}{2} = \frac{7}{8}$.
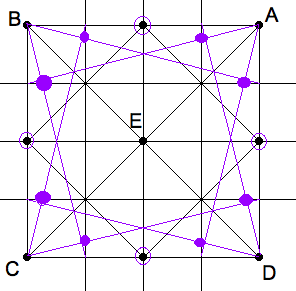
|
Each corner shoots twice across 4-by-1 rectangles to find 8 more points. |
So, in perspective, after subdividing the perspective square once,
we obtain 4 of the 12 points on the perspective circle. Subdividing
again, and shooting the corners we could obtain up to 8 more reference
points on the circle. Of course, only those in the largest quadrilaterals
are important, if you can trust yourself to get along with just 8 points
on the circle.
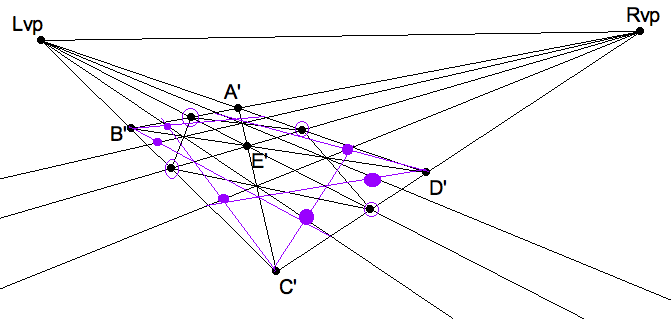
|
The back corner is too small to shoot. The 10 points suffice. |
In practice, one can usually skip the back seven-eighths points and
still sketch a tolerably good circle in perspective.



