The second problem, completing and edge and face to a cube, can also be understood in terms of tilting a right triangle about its hypotenuse into the picture plane. Suppose you are looking at the corner of a cube in space so that three faces are visible. Imagine these faces extended away from the corner, and then translate this triangular cone to your eye. Imagine looking through a tiny hole in the corner of a room, into the room.
|
A cube translated to the eye. |
This sight cone of the cube crosses the picture plane on the framing triangle whose vertices are the three vanishing points of the edges of the cube. The three edges of the framing triangle are the horizon lines for the faces of the cube. Now tilt each of the right triangles which the picture plane cuts from the sight cone, into the picture plane. Here you see the sight cone
|
The sight cone opening up like barnacle. |
opening up like a barnacle, as its faces tilt to the outside of the framing triangle. You could also collapse the sight cone to the inside of the framing triangle, as is done in some "theories of perspective" in the classical literature.
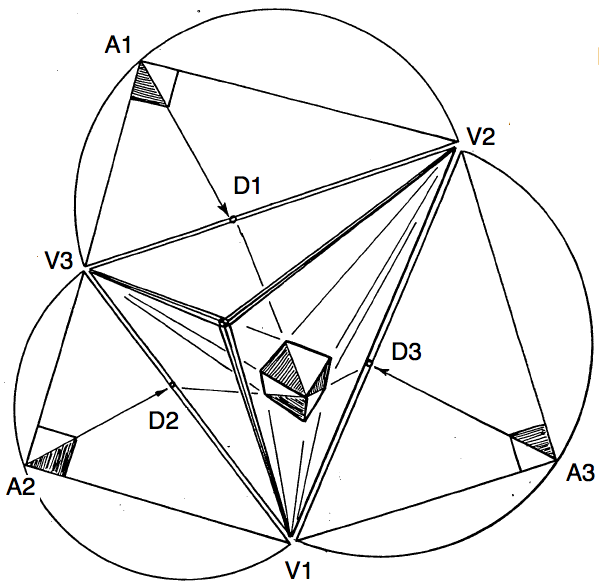
A moment of geometrical reflection reveals a remarkable set of coincidences. If you prolong the three altitudes into the framing triangle they pass through the focal center on their way to the zeniths at the opposite vertices. The point where the altitudes of a triangle meet is known as the orthocenter. In other words, the orthocenter of an acute triangle, is also the focal center of a perspective view for which opposite vertex-edge pairs are the zenith-horizon pairs of mutually orthogonal planes.
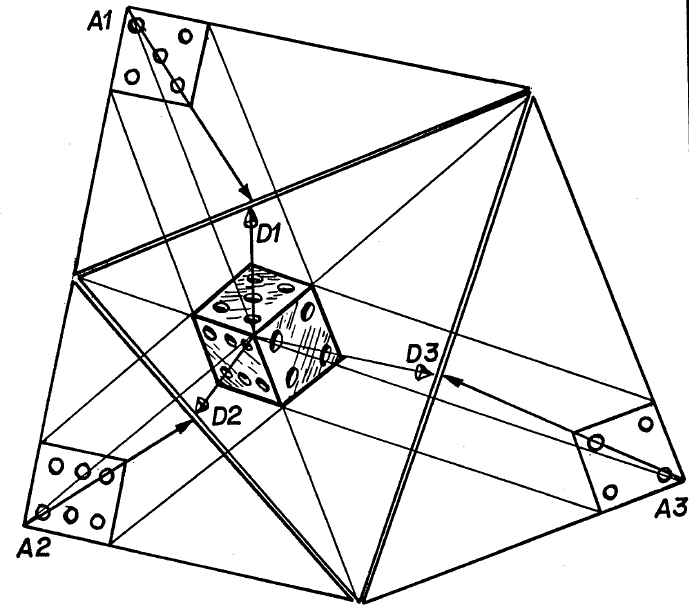
The figure above an orthographic drawing of a die placed into the apex of the sight cone. The position of the three visible faces after they have been tilted into the picture plane are drawn on the outside of the framing triangle. Note how the three diagonal vanishing points, $ D_1, D_2, D_3 $ can be located on the framing triangle by prolonging the diagonals of the three little squares from $ A_i $ to $ D_i, i=1,2,3 $.
|
Cube in 3 point perspective inside its framing triangle. |
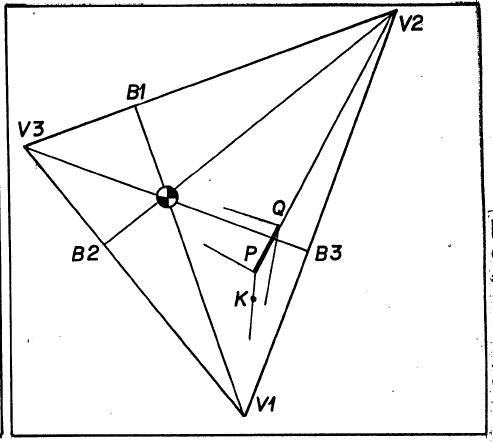
With all this understood, you are ready for a recipe that completes the cube given the picture plane location of the nearest vertex $ P $ , an edge $ PQ $, and the horizon line for one face containing this edge.
|
Cube, given edge, horizon, eypoint and focal distance. |
|
Constructing the perspective frame for the cube. |
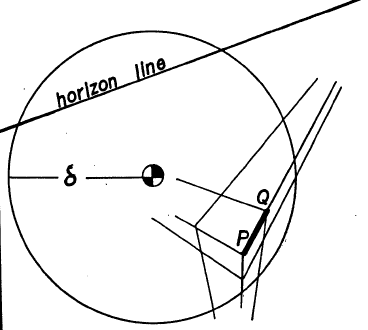
Construct the zenith $ V_1$ for the given horizon using the given focal disc. Label the base point $ B_1 $.
Prolong the given edge $ PQ $ till it crosses the horizon line at vanishing point $ V_2 $. These two constructions are still independent. You could do $ V_2 $ first.
Prolong the perpendicular from the edge $ V_1 V_2 $ through the focal center to find the third vertex, $ V3 $ , of the framing triangle. The four lines, $ PV_2, PV_3, QV_1, QV_3 $ depict the corner of an infinite slab which is one edge-unit thick. To carve a cube from this, we need a second corner, $ K $ nearest $ V_1 $ for example. But $ K $ is where $ PV_1 $ crosses the prolongation of the line from $ V_2 $ to that corner on the cube where the line $ QV_1 $ crosses the diagonal $ PD_3 $. That is what diagonal vanishing points are very good for. This produces an infinite beam, one edge-length square. As soon as you have found one more corner, say with the aid of a second diagonal vanishing point, the remaining constructions become obvious.