Horizon and Zenith

First, a brief vocabulary lesson. In the real 3D world, the horizon is an apparent line where a flat earth meets the sky. The zenith is the direction we mean when we say "straight up". We may generalize to 3D geometry as follows. The horizon of a plane is the pencil of all planes parallel to a given plane. In Kepler’s terms, it it the ideal line corresponding to the plane. The zenith of a plane is the ideal point corresponding to the pencil of parallel lines that are perpendicular to the plane.

With Alberti we transfer these concept to a picture plane or canvas, relative to an eye in space, whose (perpendicular) distance to the canvas is the focal distance. The painter draws a horizontal line on the canvas where she sees the horizon of the ground plane. The point nearest to the eye on the canvas, hence where the perpendicular from the eye to the canvas meets that plane, is called the eye point or orthocenter.

We should be careful to understand the difference between the eye, which is a point in space not on the canvas, and the eye point, which is a point on the canvas. Also, we anticipate a supremely important propery of this point by calling it the orthocenter, since that terms properly means the point where the altitudes of a triangle meet.

The zenith point on the canvas is where the line perpendicular to the ground plane pierces the canvas. If the canvas happens to be vertical (a window pane, for example) then the zenith line is parallel to the canvas. In that case, the zenith point is an ideal point in the canvas.

The vanishing point of a line is the point in the canvas that a the eye ray for the line meets the canvas. The eye ray of a line in space is the line through the eye which is parallel to it. In effect, it is where the one-eyed painter sees the line meet the plane at infinity. Horizontal lines all vanish on a point on the hozion line.

Finally, when the context makes it clear that we’re talking about the picture of the horizon, eye, and zenith in the canvas, we will be sloppy and say things like "two parallel lines meet at their common vanishing point".

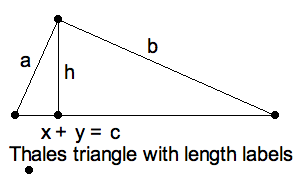
Around -600, Thales of Miletus collected a number of geometrical theorems and also gave something like proofs for them. He is considered to be the founder of Greek mathematics as a deductive science, based on logic rather than miscellaneous observation. One of these says that a triangle inscribed in a semicircle, with the diameter for a side, must be a right triangle. Later, geometers noticed that dropping the altitude from the right angle to the hypotenuse divided the right triangle into two additional similar right triangles. Labeled as shown in the figure, $ \triangle abc ~ \triangle xha ~ \triangle hyb $, and in that order: short - long - hypotenuse.

From $ \frac{shrt}{hyp} = \frac{x}{a} = \frac{a}{c} $ and the analogous comparison $ \frac{long}{hyp} = \frac{y}{b} = \frac{b}{c} $ we have

But for our present purposes, we want another comparison, $ \frac{shrt}{long} = \frac{x}{h} = \frac{h}{y} $ , from which we see that $ h^2 = xy $ or, more interesting, $ h = \sqrt{xy} $. For the Greeks, a segment $ h $ is the geometric mean of two segments $ x, y $ means that $ \frac{x}{h}=\frac{h}{y} $. Today we say its the square-root of the product.

Thales' triangle, or equivalently, the geometric mean, reappears repeatedly in the art of perspective drawing. We present three examples:

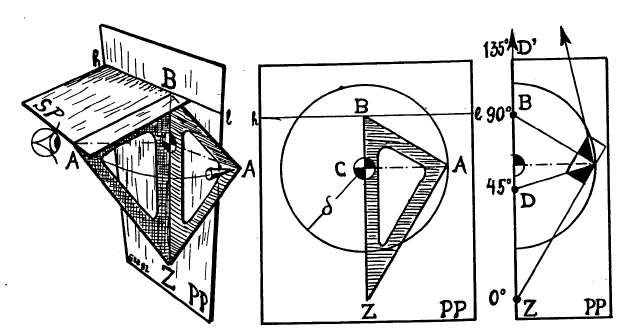
To solve the horizon-zenith problem, let’s analyze the situation from a third-party view (left detail in the figure.). A right triangle, $ \triangle BAZ $, has been placed between picture plane, $ PP $ and eye of the observer:

In the same detail, we lay this right triangle into the picture plane by rotating it about the hypotenuse. The middle details is a view of the canvas, as the artist is sees the picture plane. The interior of the circle centered at $ C $ of radius $ \delta $ corresponds to a $ 90^\circ $ visual cone from the eye point. Artists try to put most of their important details into this disc because objects have less perspective distortion there than outside the disk.

Now, if we consider the sight plane $ SP $ a "horizontal", i.e. parallel to the ground plane, then the line $ (AZ) $, being "vertical", points to the "zenith", which is directly overhead. This line pierces the canvas at $ Z $, and so we call $ Z $ zenith point corresponding to the given horizon line.

To synthesize this construction in a picture plane, rotate the triangle about its hypotenuse. For now I shall assume that the focal disc is given, and tell you later how to determine it from other clues in a given picture. For any horizon line $h$, erect a right triangle with one acute angle at $ B $, the foot of the perpendicular from the orthocenter to the horizon. The apex $ A $ is on the focal circle. The other end of the hypotenuse is the zenith point for $ h $ . The principal use of the zenith point is to draw vertical lines in perspecive:

Incidentally, we can use this right triangle to find the vanishing points on $ (BZ) $ of lines that are inclined at other angles to the vertical, such as the $ 45^\circ $ point $ D $ and the $ 135^\circ $ point $ D' $ (right detail). These two points are significant because they correspond to vanishing points for diagonals of a square in space whose sides vanish at $ B $ and $ Z $. We will meet such diagonal points again in subsequent constructions.

We close this section by posing some problems. We have seen above that given $ C, \delta, h $ how to find $ Z $. To show that you understand, also show how to find

by describing the construction. For a solution using a geometry drawing tool, like KSEG, GEX, GSP, Geogebra etc, create a single file with four labelled figures (use d for $\delta$, and the unknown in a different color than the other labels.

For a solution using ruler and straightedge, indicate the order in which features are constructed using subscripts. In each case, the given items receive subscript 0.