The notion that we can rigidly rotate the Euclidean plane about
any point $ Q $ and by any angle $ \theta $ without
breaking any geometric relations we value is deeply embedded in
our experience. Perhaps this is less the case today than it was
in the ancient world which did not use blackboards or projection
screens to teach geometry. Instead, we can imagine students standing
around the figures being drawn in the sand by the teacher. So
there was no notion of "up" and "down" immediately associated with
the figure. Clearly, up-down changes when we rotate the plane.
But angles, distances, incidence of points on lines, parallelism and
intersections, these do not change under rotations. Thus rotations
should join translations and reflections as isometries we wish to
study.
Regardless how intuitive a rotation may seem, it is not easy to give
an explicit formula for it. A rotation has a single fixed point.
So, to give a rigorous definition we use
property R3 for reflections we studied in the previous lesson.
Note the factor of 2, and the direction of the angle:
$ \angle k \ell = \pi - \angle \ell k $. Still, there is something
arbitrary about the choice of mirrors. As we shall see presently,
this is a good thing. We can easily change the mirrors if we prefer
better ones than given.
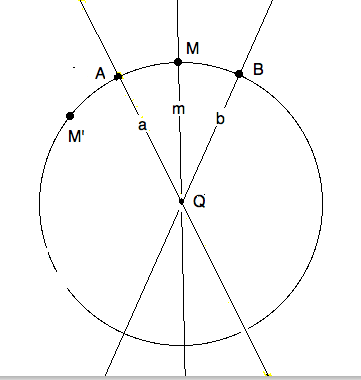
For instance, given the rotation $ \rho_{Q,\theta} $ and
any desired mirror $ m = (MQ) $ where M is some point other
than $ Q $, of course. We can make $ m $ the bisector
of an angle $ \theta = \angle BQA = \angle ba $ in two ways.
We are using the mnemonic "A,a" for "after" and "B,b" for "before".
-
Draw $ b $ so that $ \angle bm = \frac{1}{2}\theta $.
Then reflect $ b $ in $ m $ to get $ a $.
-
Define $ a = \rho_{Q, \frac{1}{2}\theta}(m) $ and
$ \rho_{Q,-\frac{1}{2}\theta} (m) = b $. Note "half angle"
and its sign.
|
Twas brillig and the slithy toves did gyre and gimble in the wabe. |
Question 1.
Why is $ \rho \ne \sigma_m $ ?
Apply both isometries to the point $ M $ on $ m $. The
RHS leaves the point fixed. If the LHS would also fix $ M $ then
the rotation would have more than one fixed point. Indeed, you can
see in the figure that $ M^\rho = M' $ was moved.
Proof: From the answer to question 1 we know that
$ \alpha := \sigma_m \rho $ is not the identity. So property
R2 applies since $ \alpha $ has two fixed points, $ Q $ and
$ B $, namely that $ \alpha = \sigma_{(BQ) $. Hence
$ \sigma_m \rho = \sigma_b \implies \rho = \sigma_m \sigma_b $.
A similar argument for $ \omega = \rho \sigma_m $ settles the
"after mirror" cases. (Do it!)
An immediate application of this theorem and the conjugacy theorem for
reflections (CTR) is this extension of CTR to rotations.
Proof: Factor $ \rho = \sigma_\ell \sigma_k$. Then
$ \alpha \sigma_\ell \sigma_k \alpha^{-1}
= \alpha \sigma_\ell \iota \sigma_k \alpha^{-1}
= \alpha \sigma_\ell \alpha^{-1} \alpha \sigma_k \alpha^{-1}
= \sigma_{\ell^\alpha} \sigma_{k^\alpha} $
where we applied CTR in the last equation. Note that the mirrors
moved by $ \alpha $ intersect at $ Q^\alpha $. Since
isometries preserve the dot product of vectors, they preserve the
cosine of the angles. So, although the signed angle itself may not
be preserved, its absolute value is.
Consider a signed angle $\angle PQR $ under an isometry
$\alpha$. It’s image must be $\angle P^\alpha Q^\alpha R^\alpha $.
If the isometry reverses orientation, as for a reflection in a line, then
the image angle has the opposite sense; cyclic goes to clockwise, and vice
versa. This handedness of an isometry is determined by the parity of the number
of mirrors it decomposes into; and the composition of an even number of
mirrors yields an orientation preserving isometry, and the composition of
an odd number of mirrors yields an orientation reversing isometry.
As we shall prove presently, translations and rotations are orientation
preserving. Reflections and gliders are oriention reversing.
