In this lesson we define the ultimate building block, the
atoms among the isometries. These are the reflections in
lines, and unlike the transformations we have studied so far,
they do not have a simple formula in vector algebra, like
dilatations, translations, and central reflections.
The concept is simple enough. To reflect a point $ X $
across a line $ \ell $, drop the perpendicular from
$ X $ to $ \ell $ and extend it an equal distance
to the other side of the line. This point transformation is aptly
called a reflection, because if $ \ell $ is considered
to be a mirror, then the reflected object would look as if it
were on the "other side" of the mirror.
A point on the mirror line is moved
to itself, i.e. it is a fixed point of the reflection. In fact,
we will soon see that all the fixed
points of a reflection $ \sigma_\ell $
lie on the mirror line $ \ell $ of the reflection.
A reflection does not have an easy, explicit formula that defines it,
and so is a new kind of transformation. A graphics computer requires a
formula, however, and we next develop one, which might more aptly be
called a recipe for a formula, which a computer would be just as
happy to use as a single equation.
We begin by emulating Euclid and KSEG with two points, $ A $
and $ B $, that determine the mirror line
$ \ell = \ell_{AB} $. This
choice is obviously not unique. If we make no further restrictions
on which points, and for what lines, then the explicit formula is
fierce indeed:
|
$ \sigma_{\ell_{AB}}(X) = 2A-X+2\frac{(X-A)(B-A)}{(B-A)(B-A)}(B-A) $ |
(1) |
where the scaling of the displacement vector $ (B-A) $
is the ratio of two dot-products. You should recognize the $ 2A-X $
to be a central reflection of X in $ A $, $ \sigma_A(X)$.
The properly scaled displacement
vector is nothing but the projection of $ X-A $ to the mirror line.
Thus the geometrical meaning of formula (1) is here:
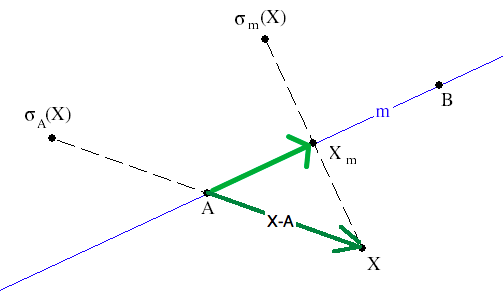
|
Geometrical interpretation of the formula for a reflection in a line. |
To see where the projection formula comes from, let’s recall some facts about vectors.
$F\frac{D}{|D|}=|F|\ cos\angle FD$ |
gives the magnitude of the projection of $F$ in the direction of $D$.
`F_D\ =\ (F frac{D}{|D|})frac{D}{|D|}\ =\ frac{F D}{D D}D`. |
`F_D` is called the `D`-component of `F`.
- The component of `F` in the direction perpendicular
to `D` is given by the formula `F_D^{_|_}=F-F_D`.
We may denote this component by `F_D^{_|_}` and also by
`F_{D^{_|_}}`. The first is the vector $ F_D $ turned
$ 90^\circ $ to the right. The second is the component of $ F $
in the directions `D^{_|_}`. That these two vectors are the same
requires a proof.
Proof. We must show `F_D^{_|_}=F_{D^{_|_}}`.
Rather than prove this equality directly, it’s slightly easier
to show that `F_D^{_|_}` has the same direction
and magnitude as `F_{D^{_|_}}`.
Its direction must be perpendicular to `D`:
`(F-F_D) D\ =\ F D-F_D D\ =\ F D-(frac{F D}{D D}D D)\ =\ F D-F D\ =\ 0`. |
Thus `F_D^{_|_}` is perpendicular to `D` and the component `F_D` so we may think of of `F_D^{_|_}` and `F_D` as the sides of a right triangle.
Let $ m $ be any line, called the mirror
of the reflection
$ \sigma_m $. Then for every point $ X $ on $ m $,
set $ sigma_\m(X)=X $. Thus,
every point on the line $ m $ is fixed by
$ sigma_m $. Otherwise, for points not on $ m $,
let $ X_m $ be the nearest point to $ X $ on
$ m $.
Since we want $ X_\m $ to be the midpoint of the segment
from $ X $ to $ X^\sigma $ we can solve the equation
`X_\m=frac{X+X^sigma}{2}` |
`X^sigma=2X_\m-X`. |
Note that we have seen such a formula before. It says that
$ X^\sigma = \sigma_{X_m} $.
Even though we have not given an explicit formula for $ X_m $,
we can already prove that
Proof:
By definition, to show $ \sigma = \sigma_m $
is an isometry we only need to show
that it preserves distance: $ |X^\sigma-Y^\sigma|=|X-Y| $.
Let’s compute `X^sigma-Y^sigma=(2X_\m-X)-(2Y_\m-Y)=2(X_\m-Y_\m)-(X-Y)=2((X-Y)D)D-(X-Y)`.
To make the algebra more transparent, substitute
$ Z = X-Y $ so that the right most expression of the
above equation looks like this $ 2(ZD)D-Z $.
Then to compute the length, we compute its square.
`|X^sigma-Y^sigma|^2=4(Z D)^2D^2-4(Z D)(Z D)+Z^2=4(Z D)^2-4(Z D)^2+Z^2=Z^2=|Z|^2`.
But
`|X^sigma-Y^sigma|^2=|X-Y|^2` means `sigma` is an isometry.
We should still derive the explicit equation (1), although we will rarely, if
ever, need to use it. We will rely on our geometric intuitions.
Question 1.
If we set $ F = X-A $ and $ D = \frac{B-A}{\|B-A\|}$
what part of the RHS of equation (1) is just $ F_D $ ?
$ F_D = (FD)\ D = ((X-A) \frac{B-A}{\|B-A\|}) frac{B-A}{\|B-A\|} = \frac{(X-A)(B-A)}{(B-A)(B-A)}(B-A) $.
Question 2.
Why is $ X_\m = A + F_D $ ?
Because $ \triangle AX_\m X $ is a right triangle.
Question 3.
How does this "finish" the derivations of (1)?
$ X^\sigma = 2X_\m - X = 2A - X + 2F_D $ .
Question 4.
Can you draw a picture that makes
$ X^\sigma = A + (A-X) + 2(X_\m - A) $
geometrically clear from the rules of similar triangles?
The point $ B $ is not in the figure. It can be anywhere on $ \m $ since we
only use it to find the orthogonal projection of $ F = X-A $ to $ F_\m = X_\m -A $.
Note that when $ Y = A + (A-X) $ then $ A $ is the midpoint of $ \bar{YX} $.
Finally, if the base vector is $ 2(X_\m - A) $, then $ X_\m $ is the
midpoint of the vertical leg of this right triangle. Therefore the point $ X^\sigma $
is indeed the reflection of $ X $ in $ \m $.
Let us review what we know about fixed points and isometries.
-
Every point in the plane is a fixed point of the identity $ \iota $.
-
No point of the plane is left fixed by a translation $ \tau_D $.
-
A central reflection $ \sigma_Q $ has a single fixed point, $ Q $.
-
Every point on the mirror $ \m $ of a reflection is a fixed point of
$ \sigma_m $.
Let’s see to what extent the fixed points of an isometry characterize the
transformation. By "characterize" an isometry we mean that another isometry
with the same characteristics must be the same isometry.
Proof of R1. Calculate $ |X-Q|=_1|X^\alpha - Q^\alpha|=_2|X^\alpha - Q| $ where
the $ =_1 $ expresses the definition of an isometry and
$ =_2 $ expresses the hypothesis of the assertion. In other words,
$ Q $ is equidistant from the end points of
the segment $ X X^\alpha$. But, as we have used many times before,
the locus of points equidistant from the end points of a segment
is the perpendicular bisector of the segment.
Proof of R2. Every point $ X $ on $ (PQ) $ has the form
$ X=(1-t)P+tQ, t\in RR $. Relative to some third point $ K $
not on the line, this expresses $ X $ in terms of its barycentric
coordinates relative to $ \triangle PQR $. By the Barytheorem and the
hypothesis we have
that $ X^\alpha = (1-t)P^\alpha + t Q^\alpha = (1-t)P + t Q = X$.
To actually identify $ \alpha $ as the
reflection $ \sigma_\ell $, we again use some point $ K $ not
on $ \ell $. Since $ \alpha \ne \iota $, we know that $ K $ cannot be a fixed point. Then by R1, both $ P, Q $ are on the
$ perbis(K,K^\alpha)$, hence $ \ell $ is that perpendicular
bisector. So $ K^\alpha = \sigma_\ell(K) $.
To show that $ \alpha = \sigma_\ell $ we consider
$ \omega = \sigma_\ell \alpha $ and calculate the three non-collinear
points, $ P,Q,K $ are all fixed by $ \omega $. Hence by the
"tripod theorem" $ \omega = \iota $. Multiply both sides of this
equation by $ \sigma_\ell $ yields the desired result. (Be sure you
do this multiplication in the margin when you read this sentence!)
Proof of R3.
Since $ Q $ is assumed to be the only fixed point, for any other
point $ X^\alpha \ne X $ and by R1, $ Q $ in on
$ m = perbis(X,X^\alpha) $. Now, note that
$ \omega = \sigma_m \alpha $ has two fixed points, $ P and X $.
Now, $ \omega \ne \iota $ because if it were, then
$ \alpha = \sigma_m $ which has infinitely many fixed points. Hence
R2 applies, and $ \omega = sigma_\n $, where $ n=(QX) $.
Multiplying both sides by the involution $ \sigma_m $ yields the
desired $ \alpha = \sigma_m \sigma_\n $.
Proof of R4.
We already know that
translations are the product of two reflections in parallel
mirrors, that are (both) perpendicular to the translation vector, and
half its magnitude apart.
We also know that every isometry factors into the product of an osometry
followed by a translation. By definition, an osometry fixes the origin.
So, by what we have shown above, the osometry is either
-
the identity,
-
is not the identity but has another fixed point, hence is a reflection
-
or $ O $ is its sole fixed point and factors into two reflections.
We draw our first, fundamental conclusion from the properties of reflections,
specifically from R2.
The conjugate $ \mu^\alpha $ has deep geometrical meaning, but
an immediate algebraic meaning is the degree to which the two isometries
do not commute.
Question 5.
Given two isometries
$ \alpha,\mu $, for what isometry $ \xi $ is the
equation $ \alpha \mu = \xi \alpha $ true?
Multiply both sides of the equation "on the right" by $ \alpha^{-1}$,
to get $ \alpha \mu \alpha^{-1} = \xi \alpha \alpha^{-1} = \xi $
The conjugate operation has a deeper algebraic meaning than just this.
We note, in particular, that if $ \mu \ne \iota $ , neither is its
conjugate. For suppose not, and $ \iota = \alpha \mu \alpha^{-1} $.
Multiply both sides by $ \alpha^{-1} $ on the left, and by
$ \alpha $ on the right and get a contradiction (do it!).
To conclude this section, we prove one profound theorem.
Proof: Abbreviate $ m := \ell^\alpha $. Since
$ \ell^\alpha = \alpha(\ell) $, for all $ (Mm) $ there
exists $ (L\ell) $ such that $ M = \alpha(L) $. We now apply
the LHS of the equation to the point $ M $ .
$ \alpha \sigma_{\ell} \alpha^{-1}(M) =
\alpha \sigma_{\ell}(L) =
\alpha (L) = M $.
Thus $ \alpha \sigma_{\ell} \alpha^{-1} $ has every point on
$ m $ as a fixed point, and not being the identity, it must
be the reflection in that line.
This meaning of charm is reserved for this course only. We have thus found
that the identity is not charming at all. Reflections have charm 1.
Translations have charm 2. In the next section we will discover that rotations
are equally charming as translations. We already know that no isometry is
more charming than charm 4. Actually, we will discover that 3 is as charming
as any isometries get. And the isometries with charm 3 are beautiful indeed.
