Lab Experiments for Compositions
\begin{document} Updated 21nov14 \maketitle
 \section{Introduction}
To illustrate the power of the recalibration theory we first
calculate the composition of two isometries which are simultaneously
availabe in GGB, GEX or KSEG. Later, after you understand the theortical basis of
the experiments, constructions can be helpful in discovering the composition
of two rotations.
\section{Recalibration of a translation}
Recall that the recalibration theorem for a rotation $\rho$ says that we can
choose one of the two mirrors $m$ through the center of rotation $Q$, and then
calculate the \textit {before-mirror} $b$ and the \textit{after-mirror} $a$ to that
\[ \rho = \sigma_a\sigma_m = \sigma_m\sigma_b \]
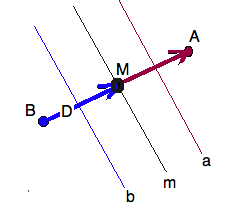
We can make the recalibration theorem for a translation $\tau$ read very
similar as follows. Choose any point in the plane $M$ and apply the
translation $A = \tau(M)$ and $B = \tau^{-1}(M)$ so that
$\tau = \tau_{A-M} = \tau_{M-B}$. Starting with mirror $m$ through $M$
and (of course) perpendicular to $(AB)$, we find before-mirror
$b = perbis(M,B)$ and after-mirror $a = perbis(A,M)$ so that the translation
factors thus \[ \tau = \sigma_a\sigma_m = \sigma_m\sigma_b \].
\section{Problem A}
Given a rotations $\rho_{Q,\theta}$ and a translation $\tau_{D}$, conduct
an experiment to discover that their composition
$\alpha =\tau_{D} \rho_{Q,\theta}$
is again a rotation.
\textbf{Hint:} Choose a mirror $m$ which can serve for both isometries, with
$a$ its after-mirror for the translation, and $b$ the before-mirror for
the rotation. Then show, experimentally, that $\alpha = \rho_{P,\theta}$, where $P=(ab)$.
\section{Introduction}
To illustrate the power of the recalibration theory we first
calculate the composition of two isometries which are simultaneously
availabe in GGB, GEX or KSEG. Later, after you understand the theortical basis of
the experiments, constructions can be helpful in discovering the composition
of two rotations.
\section{Recalibration of a translation}
Recall that the recalibration theorem for a rotation $\rho$ says that we can
choose one of the two mirrors $m$ through the center of rotation $Q$, and then
calculate the \textit {before-mirror} $b$ and the \textit{after-mirror} $a$ to that
\[ \rho = \sigma_a\sigma_m = \sigma_m\sigma_b \]
We can make the recalibration theorem for a translation $\tau$ read very
similar as follows. Choose any point in the plane $M$ and apply the
translation $A = \tau(M)$ and $B = \tau^{-1}(M)$ so that
$\tau = \tau_{A-M} = \tau_{M-B}$. Starting with mirror $m$ through $M$
and (of course) perpendicular to $(AB)$, we find before-mirror
$b = perbis(M,B)$ and after-mirror $a = perbis(A,M)$ so that the translation
factors thus \[ \tau = \sigma_a\sigma_m = \sigma_m\sigma_b \].
\section{Problem A}
Given a rotations $\rho_{Q,\theta}$ and a translation $\tau_{D}$, conduct
an experiment to discover that their composition
$\alpha =\tau_{D} \rho_{Q,\theta}$
is again a rotation.
\textbf{Hint:} Choose a mirror $m$ which can serve for both isometries, with
$a$ its after-mirror for the translation, and $b$ the before-mirror for
the rotation. Then show, experimentally, that $\alpha = \rho_{P,\theta}$, where $P=(ab)$.
Similarly, discover what $\omega =\rho_{Q,\theta}\tau_{D}$ is and in your documentation, compare $\alpha$ with $\omega$. \section{Problem B} Analyze the composition $\beta = \rho_{P,\phi} \rho_{Q,\theta}$ in a similar way as in Problem A. For this exercise, use GeoGebra. In the documentation to Problem B, determine when $\beta$ is again a rotation (determine the fixed point and the angle of rotation). Is there a case when $\beta$ is, in fact, a translation? \section{Lab Assignment} Deposit \textbf{single} PDF document describing both problems. But submit the GeoGebra (or GEX) files for each problem on the Moodle. \end{document}