Object:
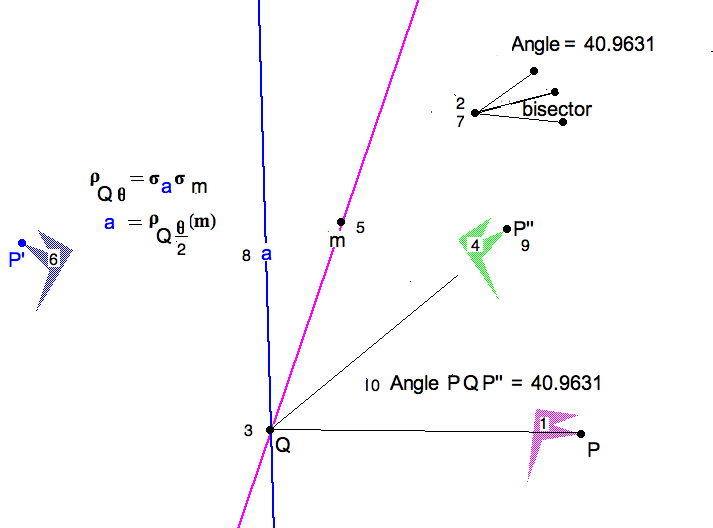
Factor a given rotation $ \rho_{Q,\theta} $ into the product of two reflections $ \rho = \sigma_a \sigma_m $, where $ m $ is a given mirror (through $ Q $ ).
-
Choose a gnomon. For example an F shaped concave hexagon. Make sure there is at least one point on the gnomon which is not hidden.
-
Give yourself an angle you can change, and later bisect.
-
Give yourself a center of rotation.
-
Rotate the F (pink to green) by the angle you made.
-
Given an arbitrary, point construct the first mirror $ m $. (Pink as well.)
-
Reflect the pink gnomon to the blue gnomon. Liberally wiggle the "givens" to see what depends on what.
-
Bisect the angle of rotation. You'll need half that angle.
-
Advance $ m $ to the after-line $ a $ by rotating $ m $ about $ Q $ by half the angle: $ a = \rho_{\theta/2}(m) $ .
-
Reflect the reflection in the blue mirror $ a $. BEHOLD !, it fits right on top of the rotated gnomon. You can follow the fate of point $ P $ to $ P' $ to $P''$.
-
Measure the angle $ PQP'' $ to see that it really is the angle we chose for our rotation. Wiggle the primitives vigorously to convince yourself of the truth of this theorem.
We called the mirror $ a $ for "after-mirror". Suppose we wanted to find a before-mirror $ b $ so that $ \rho =\sigma_m \sigma_b $. How would we do this? Submit a solution to this corollary consisting of the .ggb file and an (annotated) .png of your figure to the Moodle, when directed to do so.