Euler Line Construction
26sep13 updated for GEX2.0 with the help of Liz Denz and Boyang Guan\begin{document} \maketitle
 \section{Introduction and Purpose of this Lesson}
Most of the students in the class can use the GEX2.0 drawing package and the
Paint/iPaint method described in Advice to create usable figures. In this
lab we will apply these skills to construct Euler's Line and Feuerbach's
Ninepoint circle. Since this lesson is frequently used as an introduction
to GEX2.0, the instructions are given in full detail. Experienced readers can
proceed more quickly on their own.
\subsection{What you hand in to complete this lab.}
\begin{itemize}
\item A labeled \textbf{figure} (.png file) illustrating Euler's Line of a triangle.
\item A GEX2.0 \textbf{construction} (.seg file) showing Feuerbach's circle.
\item You should complete the figure in the lab, but you may finish it at home.
\item You should complete the construction at home, but you may submit it in
class if you are done.
\end{itemize}
\section{ Euler Line }
\begin{itemize}
\item In GEX2.0, create triangle $\triangle ABC$ in cyclic (=counter-clockwise) order.
Note that GEX labels points and line sequentially. There is a sophisticated text entry tool under the (A)-button in the Create palette. We will discuss this advanced feature later. Be aware that the labels in this document may not coincide with the lables created in your session. Set up a translation table on a piece of scratch paper.
\item Construct the centroid $G$. You'll need only two medians for this
because you already know from the Centroid theorem that the third median goes
through the same point. Since you'll need construct $G$, select the two medians
and click on the intersection button. Then hide the medians, but not the centroid.
\item Construct the circumcenter $D$. The \textit{circumcenter} is the center of the unique
circle $\bigcirc ABC$ which passed through all three vertices of the triangle.
Recall from high school geometry that the perpendicular bisector of every secant of
a circle passes through the center. Hence, you'll need two perbises (= perpendicular
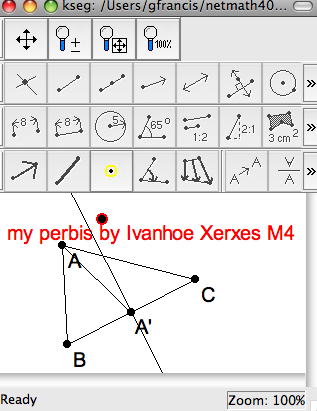
bisector, for short) on the sides of the triangle to find their intersections point.
\item Extend the segment $DG$ to twice its length beyond $G$ to a point $H$.
That is $ H-G = 2(G-D)$. In a ruler and compass
construction you would use the compass to mark off the required distances. You
could do this in GEX2.0 by choosing a $H\ell_{DG}$ and moving it into the correct
place by measuring. This is the wrong way to do this.
\item Mark the vector $G-D$ with tail $D$ and head $G$ as a transformation. Then
translate the segment $DG$ twice to find $H$. This construction is more in the
spirit of Euclid's second postulate, which says that you can extend a line segement
indefinitely.
\item Construct (or unhide) one median. Say it's $(AA')$. Construct the line
segments $A'D$ and $AH$.
\item This reveals two similar triangles, one twice as big as the other. Verify
that they are similar by measuring two pairs of angles. Warning: angles in GEX2.0
are oriented, and need to be measured in the cyclic order. And angle of 330
degrees is a negative angle of 30 degrees.
\item Conclude that lines $(AH)$ and $(A'D)$ are parallel. This follows from
a theorem on parallel lines and opposite-interios angles of a transversal. You
learned this in high school geometry. Experimentally, by could construct the
parallel to $(A'D)$ through $H$ and see that it goes through $A$.
\item This shows that the line $(AH)$ is an altitude. And, by imagining the same
construction with starting with the other two medians, we have that the $H$ lies
on all three altitudes. This point is called the \textit{orthocenter} of the
triangle.
\item Take a screen shot of this figure for further processing with iPaint/Paint. See Advice if you forgot/don't know how to do this on your platform.
Note that, in GEX2.0, it may not be necessary to edit the figure outside of GEX.If you right-click the label of a point, and choose "Properties", then one of these is the label itself. This can be changed to a different letter, but also to a one-line text. This elaborate label sticks to the point when it is wiggled.
There is also a different method of creating a text-box in the figure you are drawing with GEX2.0. Using the (A)-button in the Create section of the GEX palette you can create a text box and write text into it. This is, however, not attached to any point or line, and so is not affected by wiggling the figure.
\item Wiggle this GEX2.0 construction and see what happens when
$\triangle ABC$ becomes obtuse. Take another screen shot.
\item Save your GEX2.0 file as a .gex file, named "schnitzel-eulerline.gex" except
that you use your own name, which is probalby not Rudolf Schnitzel.
\item Edit your screen shots by putting your name into it and labelling the
Euler line and its three important points $G,D,H$. This will be a .png or
a .bumb file.
\item Submit the figure and the GEX2.0 file before you leave.
\item [In 2011] Submit one .png file, either the acute one or the
obtuse one, in a so-marked bin. Submit the next construction, as
a .gex file, in another; both on Moodle.
\end{itemize}
\section{Feuerbach's Ninepoint Circle}
For homework from this lab, complete a construction of the 9-point circle and
submit it to the Moodle as a .gex file, not as a figure. This circle has the
remarkable property of passing though all three of the midpoints of the
sides, all three of the bases of the altitudes, and it bisects the segment
on each altitude from its vertex to the orthocenter.
Any three of these points suffice to define a circle, and GEX2.0 will oblige
by drawing a circle through any three of these points you choose. But we
are used to thinking of a circle as determined by its center and radius.
We read off the radius from its center and one point in its circumference.
So we need the center.
Make a copy of your Euler line construction. That saves time.
Load it into GEX2.0, and keep the segment $HD$ on Euler's line
from the orthocenter to the circumcenter. Hide the other
construction lines, and the centroid, because they are not needed here.
Construct the midpoint $N$ of $HD$, namely $N=\frac{N+D}{2}$.
To build a circle centered at $N$ with the point $A'$ on it, for example,
first choose $N$ then select it as center then choose $A'$ then
click on circle tool. (A circle is a center together with a radius
given by the other end point of the radius.)
Identifiy all nine points on this circle. For this you’ll need to draw
all three altitudes and bisect $AH,BH, CH$. This exercise should remind
you of high school biology when you dissected a frog.
\end{document}
\section{Introduction and Purpose of this Lesson}
Most of the students in the class can use the GEX2.0 drawing package and the
Paint/iPaint method described in Advice to create usable figures. In this
lab we will apply these skills to construct Euler's Line and Feuerbach's
Ninepoint circle. Since this lesson is frequently used as an introduction
to GEX2.0, the instructions are given in full detail. Experienced readers can
proceed more quickly on their own.
\subsection{What you hand in to complete this lab.}
\begin{itemize}
\item A labeled \textbf{figure} (.png file) illustrating Euler's Line of a triangle.
\item A GEX2.0 \textbf{construction} (.seg file) showing Feuerbach's circle.
\item You should complete the figure in the lab, but you may finish it at home.
\item You should complete the construction at home, but you may submit it in
class if you are done.
\end{itemize}
\section{ Euler Line }
\begin{itemize}
\item In GEX2.0, create triangle $\triangle ABC$ in cyclic (=counter-clockwise) order.
Note that GEX labels points and line sequentially. There is a sophisticated text entry tool under the (A)-button in the Create palette. We will discuss this advanced feature later. Be aware that the labels in this document may not coincide with the lables created in your session. Set up a translation table on a piece of scratch paper.
\item Construct the centroid $G$. You'll need only two medians for this
because you already know from the Centroid theorem that the third median goes
through the same point. Since you'll need construct $G$, select the two medians
and click on the intersection button. Then hide the medians, but not the centroid.
\item Construct the circumcenter $D$. The \textit{circumcenter} is the center of the unique
circle $\bigcirc ABC$ which passed through all three vertices of the triangle.
Recall from high school geometry that the perpendicular bisector of every secant of
a circle passes through the center. Hence, you'll need two perbises (= perpendicular
bisector, for short) on the sides of the triangle to find their intersections point.
\item Extend the segment $DG$ to twice its length beyond $G$ to a point $H$.
That is $ H-G = 2(G-D)$. In a ruler and compass
construction you would use the compass to mark off the required distances. You
could do this in GEX2.0 by choosing a $H\ell_{DG}$ and moving it into the correct
place by measuring. This is the wrong way to do this.
\item Mark the vector $G-D$ with tail $D$ and head $G$ as a transformation. Then
translate the segment $DG$ twice to find $H$. This construction is more in the
spirit of Euclid's second postulate, which says that you can extend a line segement
indefinitely.
\item Construct (or unhide) one median. Say it's $(AA')$. Construct the line
segments $A'D$ and $AH$.
\item This reveals two similar triangles, one twice as big as the other. Verify
that they are similar by measuring two pairs of angles. Warning: angles in GEX2.0
are oriented, and need to be measured in the cyclic order. And angle of 330
degrees is a negative angle of 30 degrees.
\item Conclude that lines $(AH)$ and $(A'D)$ are parallel. This follows from
a theorem on parallel lines and opposite-interios angles of a transversal. You
learned this in high school geometry. Experimentally, by could construct the
parallel to $(A'D)$ through $H$ and see that it goes through $A$.
\item This shows that the line $(AH)$ is an altitude. And, by imagining the same
construction with starting with the other two medians, we have that the $H$ lies
on all three altitudes. This point is called the \textit{orthocenter} of the
triangle.
\item Take a screen shot of this figure for further processing with iPaint/Paint. See Advice if you forgot/don't know how to do this on your platform.
Note that, in GEX2.0, it may not be necessary to edit the figure outside of GEX.If you right-click the label of a point, and choose "Properties", then one of these is the label itself. This can be changed to a different letter, but also to a one-line text. This elaborate label sticks to the point when it is wiggled.
There is also a different method of creating a text-box in the figure you are drawing with GEX2.0. Using the (A)-button in the Create section of the GEX palette you can create a text box and write text into it. This is, however, not attached to any point or line, and so is not affected by wiggling the figure.
\item Wiggle this GEX2.0 construction and see what happens when
$\triangle ABC$ becomes obtuse. Take another screen shot.
\item Save your GEX2.0 file as a .gex file, named "schnitzel-eulerline.gex" except
that you use your own name, which is probalby not Rudolf Schnitzel.
\item Edit your screen shots by putting your name into it and labelling the
Euler line and its three important points $G,D,H$. This will be a .png or
a .bumb file.
\item Submit the figure and the GEX2.0 file before you leave.
\item [In 2011] Submit one .png file, either the acute one or the
obtuse one, in a so-marked bin. Submit the next construction, as
a .gex file, in another; both on Moodle.
\end{itemize}
\section{Feuerbach's Ninepoint Circle}
For homework from this lab, complete a construction of the 9-point circle and
submit it to the Moodle as a .gex file, not as a figure. This circle has the
remarkable property of passing though all three of the midpoints of the
sides, all three of the bases of the altitudes, and it bisects the segment
on each altitude from its vertex to the orthocenter.
Any three of these points suffice to define a circle, and GEX2.0 will oblige
by drawing a circle through any three of these points you choose. But we
are used to thinking of a circle as determined by its center and radius.
We read off the radius from its center and one point in its circumference.
So we need the center.
Make a copy of your Euler line construction. That saves time.
Load it into GEX2.0, and keep the segment $HD$ on Euler's line
from the orthocenter to the circumcenter. Hide the other
construction lines, and the centroid, because they are not needed here.
Construct the midpoint $N$ of $HD$, namely $N=\frac{N+D}{2}$.
To build a circle centered at $N$ with the point $A'$ on it, for example,
first choose $N$ then select it as center then choose $A'$ then
click on circle tool. (A circle is a center together with a radius
given by the other end point of the radius.)
Identifiy all nine points on this circle. For this you’ll need to draw
all three altitudes and bisect $AH,BH, CH$. This exercise should remind
you of high school biology when you dissected a frog.
\end{document}