After studying the two theorems in the foregoing lessons, you will have noticed their similarity. This is no coincidence; they are, in fact, equivalent. In this lesson we shall demonstrate how to derive Ceva’s theorem from that of Menelaus. What makes this proof intesting is how both directions of the "if-and-only-if" come into play. We leave for you to discover a proof for the converse, that Menelaus is also a consequence of Ceva. This is a rather challenging problem.
and
As we prove that Menelaus implies Ceva, it is clear that we can’t use the same letters for both since the same product of three ratios can’t be `+1` and `-1` at the same time. So we’ll have to get used to using different labels.
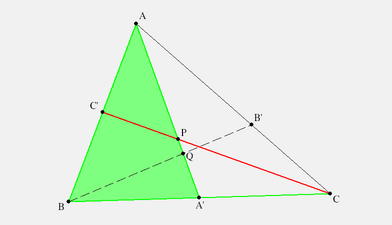
We draw a figure that is almost "true" for Ceva. We consider two triangles. First, `triangle ABA'` and line `(C C')`. Let `P=(C C')(A A')`. Since $ (PC C') $ we apply Menelaus in the $ \Rightarrow $ direction; this yields
`frac{P-A}{P-A'}frac{C'-B}{C'-A}frac{C-A'}{C-B} = +1`. |
Next consider `triangle A A'C` and line `(B B')`. Let `Q=(B B')(A A')` and apply Menelaus again to get
`frac{Q-A'}{Q-A}frac{B-C}{B-A'}frac{B'-A}{B'-C} = +1`. |
Multiplying and regrouping, we have
`(frac{P-A}{P-A'}frac{C'-B}{C'-A}frac{C-A'}{C-B})(frac{Q-A'}{Q-A}frac{B-C}{B-A'}frac{B'-A}{B'-C}) = 1` |
`(frac{P-A}{P-A'}frac{Q-A'}{Q-A})(frac{C-A'}{C-B}frac{B-C}{B-A'})(frac{B'-A}{B'-C}frac{C'-B}{C'-A})=1`. |
Now simplifying `\frac{C-A'}{C-B}frac{B-C}{B-A'}=-frac{A'-C}{A'-B}` yields
`(frac{P-A}{P-A'}frac{Q-A'}{Q-A})(-frac{A'-C}{A'-B})(frac{B'-A}{B'-C}frac{C'-B}{C'-A})=1`. |
`(**)` |
We are ready to prove Ceva. First in the $ \Rightarrow $ direction. We assume that `P=Q`, namely, that the three cevians are concurrent $ P = Q = (A A')(BB')(C C') $. Then
`frac{P-A}{P-A'}frac{Q-A'}{Q-A}=1`. |
So `(**)` reduces to Ceva’s equation (associate and multiply by $-1 $):
`(-frac{A'-C}{A'-B})(frac{B'-A}{B'-C}frac{C'-B}{C'-A})=1`. |
In the other direction, assume Ceva’s equation, namely,
`frac{A'-C}{A'-B}frac{B'-A}{B'-C}frac{C'-B}{C'-A}=-1`. |
Applying this to `(**)`, we get
`frac{P-A}{P-A'}frac{Q-A'}{Q-A}=1` |
||
`frac{P-A}{P-A'}=frac{Q-A}{Q-A'}` |
$ (** **) $ . |
Hence, `$ P=Q $`.
$\square$
Notice that we no longer supply every little step in a proof. This is intentional, since you are learning the methods we use over and over again in this exposition. The way to fill in a jump across a logical gap, is with pencil and paper. For example, for the very last step above use the MCL thus:
Express the ratio $ (** **) $ by $ \frac{x}{y} $. Recall that $ xy \ne 0 \ne x-y $. Then $ P = \frac{xA' - yA}{x-y} $, but that is also the formula for $ Q $.