This is one of the most important and versatile theorem about triangles. Its diverse proofs with differing geometrical attitudes make a good subject for this course. We shall
-
State the theorem in the language we have developed.
-
Prove it by applying Menelaus' theorem four times.
-
Show how it also follows directly from the Main Collinearity Lemma
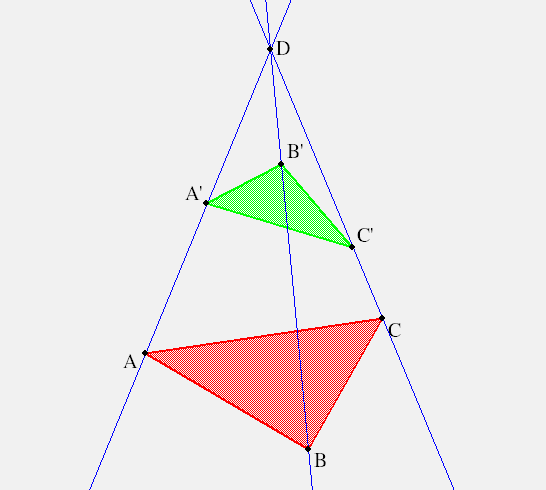
If we draw this standard oil derrick like picture for Desargues' theorem, we can read the statment and conclusion from the picture. Recall that all lines extend to infinity in both directions, even if we draw only some segments on them. The two given (green and red) triangles are said to be in a perspective position, that is, the lines through corresponding pairs of vertices are concurrent. The conclusion says that the points on corresponding pairs of sides are collinear.
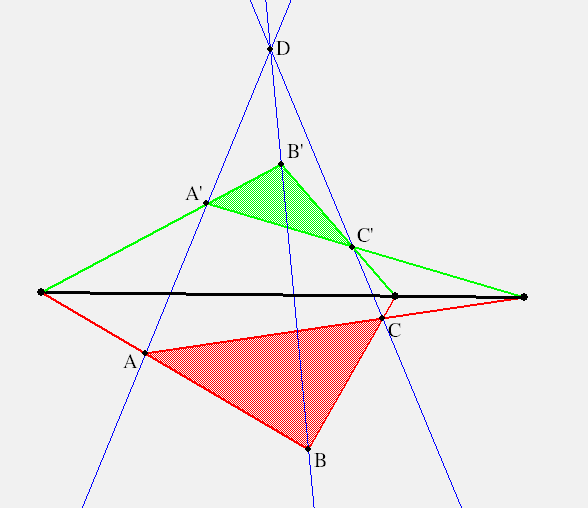
In a blank KSEG plane choose two triangles $ \triangle ABC \and \triangle A'B'C' $. Construct infinite lines $ (A A'), (BB'), (C C') $ and note that, most likely, they are not concurrent. Adjust your choice of only a few vertices (how many?) so that they do become concurrent, i.e. so that now the two triangles are in perspective. For instance, construct the point $ D = (A A')(BB') $ and maneuver $ C' $, for instance until $ D(C C') $. Consider the sides of the triangles labelled in this logical way: $ a=(BC), b=(CA), c= (AB) ; a'=(B'C'), b'=(C'A'), c'= (A'B') $, for easier reference. Now construct these infinite lines with matching color, say both $ a, a' $ are red, $ b, b' $ are green, and both $ c, c' $ are blue. Consider the black line $ d = (a a')(b b') $ and note that it passes through the point $ (c c') $. Thus, you have experimentally verified that $ d(c c') $ if and only if $ D(C C') $.
The foregoing drawing exercise illustrates a property of Desargues' theorem called self-duality. That means, the theorem remains true if points and lines are interchanged. Consider this converse of Desargues' theorem.
Can you reformulate the statement of Desargues' Theorem to match the style in the Dual Formulation?
For a pair of 3 non-collinear points, $ \triangle ABC , \triangle A'B'C' $, we have that
$ (A A')(B B')(C C') \implies (a a')(b b')(c c') $
where $ a=(BC), b=(CA), c=(AB); a'=(B'C'), b'=(C'A'), c'=(A'B') $.
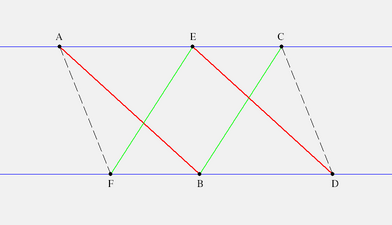
Menelaus implies Desargues
Let `(C^{**}A'B')` be a Menelaus line for △`ABD`. Note that `C^{**}(AB)`, `A'(DA)`, and `B'(DB)` so by Menelaus' Theorem,
`frac{C^{**}-A}{C^{**}-B}frac{B'-B}{B'-D}frac{A'-D}{A'-A}=+1`. |
Cycling the letters yields two more equations,
`frac{A^{**}-B}{A^{**}-C}frac{C'-C}{C'-D}frac{B'-D}{B'-B}=+1`, |
`frac{B^{**}-C}{B^{**}-A}frac{A'-A}{A'-D}frac{C'-D}{C'-C}=+1`. |
Multiplying these together and cancelling we get,
`(frac{C^{**}-A}{C^{**}-B}frac{B'-B}{B'-D}frac{A'-D}{A'-A})(frac{A^{**}-B}{A^{**}-C}frac{C'-C}{C'-D}frac{B'-D}{B'-B})(frac{B^{**}-C}{B^{**}-A}frac{A'-A}{A'-D}frac{C'-D}{C'-C})=1` |
||
`frac{C^{**}-A}{C^{**}-B}frac{A^{**}-B}{A^{**}-C}frac{B^{**}-C}{B^{**}-A}=1`. |
(*) |
Since there is a △`ABC`, and by definition, `A^{**}(BC)`, `B^{**}(CA)`, and `C^{**}(AB)`, equation `(**)\ rArr\ (A^{**}B^{**}C^{**})` by Menelaus' Theorem.
To learn this proof you should sketch (or load into KSEG) the "Oil Derrick Position" of Desargues' figure. After completing the labelling (the starred points!) pick out the various Menelaus figures this proof depends on.
Tondeur’s Proof
Since Menelaus was proved using the Main Collinearity Lemma, and Menelaus implies Desargues, we would expect there to be a direct proof of Desargues' theorem from the Main Collinearity Lemma. And here it is.
Since `(DA A')` (i.e. they are collinear), `D=aA+a'A'` with `a+a'=1`. Also `(DB B')`, so `D=bB+b'B'` and `b+b'=1`
Putting these together,
`D=aA+a'A'=bB+b'B'` |
`aA-bB=b'B'-a'A'` |
Recall that barycentric coordinates must add to $ 1 $. So `0= 1-1= (a+a')-(b+b')=(a-b)-(b'-a')` and so `(a-b)=(b'-a')`. Hence, "dividing equals by equals", obtain
`frac{aA-bB}{a-b}=frac{b'B'-a'A'}{b'-a'} = C^(**) ` |
Call this point `C^{**}` and note that `C^{**}(AB)` and `C^{**}(A'B')` so `C^{**}=(AB)(A'B')`. Clear fractions to get
`aA-bB=(a-b)C^{**}` and cycle
`bB-cC=(b-c)A^{**}`
`cC-aA=(c-a)B^{**}` and add
`0=(a-b)C^{**}+(b-c)A^{**}+(c-a)B^{**}` where `(a-b)+(b-c)+(c-a)=0`.
Therefore, by the last criterion in the MCL we that $ (A^(**) B^(**) C^(**) ) $.
Did we forget to check a hypothesis in this applications of MCL?
We did. We must make sure that the cofficients are not zero, i.e. that $ (a-b)(b-c)(c-a) \ne 0 $. But check the facts. If $ a=b $ then $ a+a'=1 $ and $ b+b'=1 $ would lead to $ a' = b' $ and $ A=B $. This is forbidden by the hypothesis, $ \triangle ABC $.