Summary Lesson on Euler's Line and Menelaus' Theorem
3oct10\begin{document} \maketitle
 \section{Introduction}
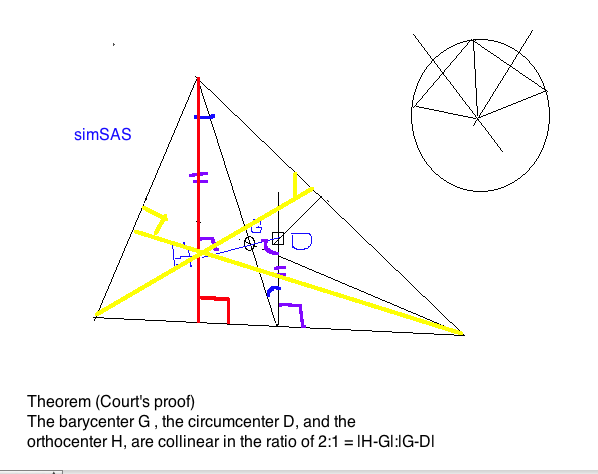
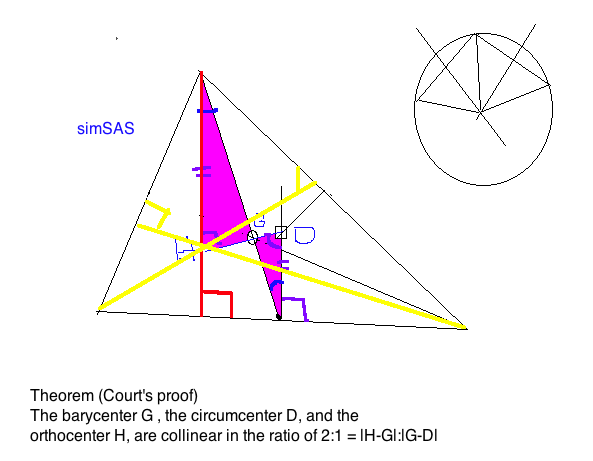
We reviewed the lab experiment constructing the Euler line
according to Court's proof that the altitudes of a triangle are
concurrent. A brief review of the Lesson A8 (in the notes) that
Menelaus' Theorem implies Ceva's Theorem is illustrated by a screen shot
from the class.
\section{Court's Proof and the Euler Line}
\section{Introduction}
We reviewed the lab experiment constructing the Euler line
according to Court's proof that the altitudes of a triangle are
concurrent. A brief review of the Lesson A8 (in the notes) that
Menelaus' Theorem implies Ceva's Theorem is illustrated by a screen shot
from the class.
\section{Court's Proof and the Euler Line}
 See Section 2 of the original lesson on dilatations online
at MA403 portal page > Class Webpages > Dilatations. In this edition
of the course we shall not cover the remainder of this lesson, and
substitute an abbreviated version on W6 with an active learning session
on F6 on the same subject.
\section{Menelaus implies Ceva}
See Section 2 of the original lesson on dilatations online
at MA403 portal page > Class Webpages > Dilatations. In this edition
of the course we shall not cover the remainder of this lesson, and
substitute an abbreviated version on W6 with an active learning session
on F6 on the same subject.
\section{Menelaus implies Ceva}
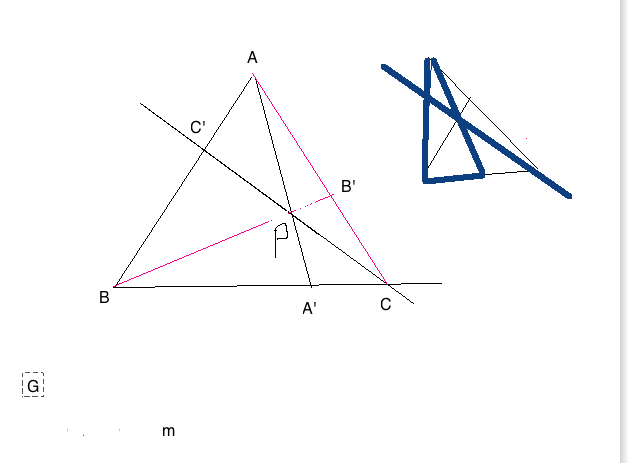 This very short lesson at
MA403 portal page > Class Webpages > Affine > A8
is left to the student. You should work through the proof and write it
up in your journal. This is a typical question on the final for this course.
In the picture, the point is that inside the figure for Ceva, there are
three similar Menelaus figures. The screen shot shows one of them. The
labelling is intentionally left off, and you should supply the labels
correctly.
\end{document}
This very short lesson at
MA403 portal page > Class Webpages > Affine > A8
is left to the student. You should work through the proof and write it
up in your journal. This is a typical question on the final for this course.
In the picture, the point is that inside the figure for Ceva, there are
three similar Menelaus figures. The screen shot shows one of them. The
labelling is intentionally left off, and you should supply the labels
correctly.
\end{document}