15mar11
\section{How to study this section of the course}
\subsection{Lesson of Models}
The Lesson on Models is an introduction to the two most important models
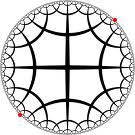
of non-Euclidean geometry, the \textit{ Beltrami-Klein Model}, and the \textit{ Poincare-disk Model}.
The former is generally just called the "Klein model", and the latter is also
on of the two \textit{ conformal } models associated with Poincar\'e's name.
By "conformal" we mean "angle preserving". Both are also referred to as
"hyperbolic models" because \textit{ Hyperbolic geometry} is a synonym for
\textit{ Non-Euclidean geometry}. There are better reasons for all this
redundancy of nomenclature, but we won't give them here. Google them!
The thing to memorize is that both models are \textbf{ inside} the unit
disk. The Cartesian points on the boundary and outside of the disk are
still there, the are just not part of the model; they a points, but not
Points. In the Klein model, straight Lines are (segments) of straight
lines (which is useful). In the Poincare model Angles have the same
measure as Euclidean angles (which is useful for other purposes.)
On the other hand, in the former it is hard to construct and impossible
to recognize Right Angles. In the latter is hard to connect two Points
by a Line, unless the Line is a diameter of the disk. So, even in the
Poincare model some Lines are lines, but only if they're diameters.
\subsection{Capitalization}
At this point we abandon a strict adherence to the convention of
capitalizing unless it is useful to make the distinctions. So the
context determines in which geometry we're talking.
\subsection{Circle Inversion}
The first lesson introduces, and Bakshy's notes develop,
the concept of \textit{ circle inversion }. This
generalizes the concept of \textit{reflections} in a straight line
you studied in analytic geometry. It is possible to study non-Euclidean
geometry strictly axiomatically (which we do not do). For this you don't
need models at all. The published (independent) discoverers of
non-Euclidean geometry, Gauss, Bolyai and Lobachevsky did entirely without
models. It was Beltrami who developed the first models, and Klein who
knew how to adapt them to school geometry.
It is also possible to treat the models srictly in terms of analytic
geometry, for which you need the concept of circle inversion defined
analytically. Hvidsten's book permits such an approach, but we do not
take it. You should study Bakshy's condensation for your own edification.
We will use a few excerpts from it.
\section{The Complex Plane}
Hvidsten introduces the essentials fo the complex plane at the end of
his chapter on Cartesian geometry. They are developed and applied later
in Chapter 8. This chapter was written at an almost graduate-level and
needs to be explained. That is the approach we take here. But we do not
complete Chapter 8 in this course. My intention is to get you to a
plateau of comprehension so that you can profitably complete the chapter
on your own at some later time when you get bored with the vapid math
all around you.
\subsection{Moebius Transformations}
Felix Klein originated the modern concept that all geometry is based,
ultimately, on groups of transformations. This is the properly developed
in the sister course, netMA403. The astronomer, geometer and physicist,
August Ferdinand Moebius is famous for much more than the strip of paper,
glued together after a half-twist. Indeed, he \textit{ used} this artefact
as an example. It was known to the Greeks and used by medieval farmers, and
engineers of the industrial age to make drive belts wear evenly
on "both" sides (since they had only one side! to wear).
For the record, and this belongs into an elementary topology course,
M\"obius (as you would write it in LaTeX) proposed gluing a flexible
disk to a (very) flexible Moebius band, thereby closing it up into a
one-sided "sphere". This object becomes a model (in four space) of
\textit{ projective geometry}, which is another subject introduced in
MA403. The last undergraduate course in Projective Geometry at the
University of Illinois died in the '70s.
[This introductory/guide will be continued.]
\section{Unfinished Lessons}
The 5 lessons in .pdf form are transcripts of interacive session in
a class using a tablet computer. I expect we will replace these with
Elluminate sessions. But they could still stand to be written up by
somebody.
Overview of Lessons on Models SP11
\textit{ $\C$ 2010, Prof. George K. Francis, Mathematics Department, University of Illinois} \begin{document} \maketitle
\section{How to study this section of the course}
\subsection{Lesson of Models}
The Lesson on Models is an introduction to the two most important models
of non-Euclidean geometry, the \textit{ Beltrami-Klein Model}, and the \textit{ Poincare-disk Model}.
The former is generally just called the "Klein model", and the latter is also
on of the two \textit{ conformal } models associated with Poincar\'e's name.
By "conformal" we mean "angle preserving". Both are also referred to as
"hyperbolic models" because \textit{ Hyperbolic geometry} is a synonym for
\textit{ Non-Euclidean geometry}. There are better reasons for all this
redundancy of nomenclature, but we won't give them here. Google them!
The thing to memorize is that both models are \textbf{ inside} the unit
disk. The Cartesian points on the boundary and outside of the disk are
still there, the are just not part of the model; they a points, but not
Points. In the Klein model, straight Lines are (segments) of straight
lines (which is useful). In the Poincare model Angles have the same
measure as Euclidean angles (which is useful for other purposes.)
On the other hand, in the former it is hard to construct and impossible
to recognize Right Angles. In the latter is hard to connect two Points
by a Line, unless the Line is a diameter of the disk. So, even in the
Poincare model some Lines are lines, but only if they're diameters.
\subsection{Capitalization}
At this point we abandon a strict adherence to the convention of
capitalizing unless it is useful to make the distinctions. So the
context determines in which geometry we're talking.
\subsection{Circle Inversion}
The first lesson introduces, and Bakshy's notes develop,
the concept of \textit{ circle inversion }. This
generalizes the concept of \textit{reflections} in a straight line
you studied in analytic geometry. It is possible to study non-Euclidean
geometry strictly axiomatically (which we do not do). For this you don't
need models at all. The published (independent) discoverers of
non-Euclidean geometry, Gauss, Bolyai and Lobachevsky did entirely without
models. It was Beltrami who developed the first models, and Klein who
knew how to adapt them to school geometry.
It is also possible to treat the models srictly in terms of analytic
geometry, for which you need the concept of circle inversion defined
analytically. Hvidsten's book permits such an approach, but we do not
take it. You should study Bakshy's condensation for your own edification.
We will use a few excerpts from it.
\section{The Complex Plane}
Hvidsten introduces the essentials fo the complex plane at the end of
his chapter on Cartesian geometry. They are developed and applied later
in Chapter 8. This chapter was written at an almost graduate-level and
needs to be explained. That is the approach we take here. But we do not
complete Chapter 8 in this course. My intention is to get you to a
plateau of comprehension so that you can profitably complete the chapter
on your own at some later time when you get bored with the vapid math
all around you.
\subsection{Moebius Transformations}
Felix Klein originated the modern concept that all geometry is based,
ultimately, on groups of transformations. This is the properly developed
in the sister course, netMA403. The astronomer, geometer and physicist,
August Ferdinand Moebius is famous for much more than the strip of paper,
glued together after a half-twist. Indeed, he \textit{ used} this artefact
as an example. It was known to the Greeks and used by medieval farmers, and
engineers of the industrial age to make drive belts wear evenly
on "both" sides (since they had only one side! to wear).
For the record, and this belongs into an elementary topology course,
M\"obius (as you would write it in LaTeX) proposed gluing a flexible
disk to a (very) flexible Moebius band, thereby closing it up into a
one-sided "sphere". This object becomes a model (in four space) of
\textit{ projective geometry}, which is another subject introduced in
MA403. The last undergraduate course in Projective Geometry at the
University of Illinois died in the '70s.
[This introductory/guide will be continued.]
\section{Unfinished Lessons}
The 5 lessons in .pdf form are transcripts of interacive session in
a class using a tablet computer. I expect we will replace these with
Elluminate sessions. But they could still stand to be written up by
somebody.