Lesson on Applications
\textit{ $\C$ 2010, Prof. George K. Francis, Mathematics Department,
University of Illinois}
\begin{document}
\maketitle
\section{Motivation}
In this lesson we apply the algebraic tools we have studies to geometrical
problems. We compare the algebraic proofs to their geometrical cousins.
Sometimes the one, sometimes the other kind of proof is easier. Both are
instructive.
\section{Verifying Euclid's first postulate}
We give both kind of proof of the verification that two Points in the
non-Euclidean plane are line on a unique Line. (Note the capitals).
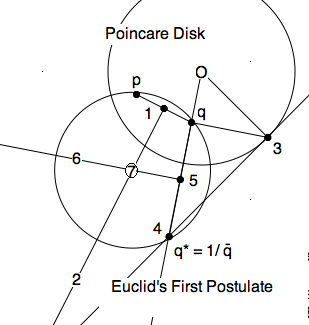
\subsection{Geometric proof}
The two Points are modelled by two points, $p,q$ in the Poincare disk.
We need a circline through $p,q$ perpendicular to the unit circle.
If the two points lie on a diameter, we're done, the diameter is the
Line they lie on. If they do not, then we need a circle through them,
which is also perpendicular to the unit circle. Here is a construction
with ruler and compass.
\begin{itemize}
\item The center of this circle must be on the perpendicular bisectore of
any two points on the circel. So far we know about only two of them. So
construct the perpendicular bisector $\ell_{12}$ of the $segment(p,q)$.
\item We know such circles are symmetric with respect to the unit circle, so
we next find the symmetric point $q*=\frac{1}{\bar{q}}$ geometrically with
Thales' construction: $\ell_{q3}$ perpendicular to $\ell_{Oq}$ and
$\ell_{34}$ perpendicular to $\ell_{q3}$ meeting $\ell_{Oq}$ at $q*$.
\item The perpendicular bisector $\ell_{56}$ to $segment(q,4)$ meets the
other bisecor at the center $7$ of the required circle.
\item The portion inside the disk is the desired $L_{pq}$.
\end{itemize}
\subsection{Algebraic proof}
On W13 we discovered the equation
\begin{eqnarray*}
z\bar{z} + \mu \bar{z} + \bar{\mu}z + 1 &=& 0 \\
|z|^2 + \Re(\mu \bar{z}) + 1 &=& 0 \\
\end{eqnarray*}
of all circles perpendicular to the unit circle, and that it is
centered at $-\mu$ (outside the unit circle), with radius-squared
equal to $|\mu|^2-1$. But all we really need to do is find the
parameter $\mu$ by substituting the two given points into the equation.
Suppose $p = x_1 + iy_1, q= x_2 + iy_2 $, then solve the two linear equation:
\begin{eqnarray*}
|z_1|^2 + \mu_x x_1 + \mu_y y_1 + 1 &=& 0 \\
|z_2|^2 + \mu_x x_2 + \mu_y y_2 + 1 &=& 0 \\
\end{eqnarray*}
for the two unknowns $\mu_x + i \mu_y = \mu$.
\subsection{Comment}
Which of these two proofs do you find the easier? Depends, if you want to
avoid learning some complex number geometry, the geometrical one is clearer.
But complex number geometry is much more versatile, since it solves other
problems too.
\section{Hyperbolic distance}
We saw why $d_H(z_0, z_1) = | \log CR(z_0,\omega_0, z_1, \omega_1)| $ was
good choice for the distance function. (I hope you can answer that now,
and it is in your journal.!) Unfortunately, for the purpose of building
the Geometry Explorer, this is computationally expensive, because it
requires finding the omega-points (on the unit circle)
of the Line through the two points. In Exercise 8.2.13, Hvidsten tells
you to compute formula which depends only on the two given points. The
lemma for this is Proposition 8.14, for which we give the followig proof:
\subsection{ Distance from the origin}
Hyperbolic geometry has no preferred points, every point is equal! But
in the Poincare model this is definitely not the case. The origin of
the disk, which an ordinary Point, is a very special point in the model.
Similarly for diameters, especially the one on the real axis. Since
hyperbolic distance is based on cross ratios, and cross ratios are
invariant under Moebius transformations, inparticular on the isometries,
we can measure distances between Points by moving their Lines into a
special position using an isometry.
To compute $d_H(0,z)$ you can either calculate
$CR(0,-\frac{z}{|z|},z,\frac{z}{|z|})$ directly because it was easy to
find the omega points for Lines that are diameters. Or, we can be clever.
Rotating the entire disk by $z \mapsto e^{-i\theta}z = |z|$, where
$\theta = \arg(z)$, is an isometry, which takes $z$ to $r=|z|$. But
now $CR(0, -1, r, 1) = \frac{1-r}{1+r} <1$ , so the distance is
$d_H(0,r) = - \log\frac{1-r}{1+r}= \log\frac{1+r}{1-r}$ as claimed. Done.
\subsection{General case}
The trick is to reduce the general case (Exercise 8.2.13) to the
particular case (Proposition 8.14). The hyperbolic translation
$ f(z) = \frac{z-z_0}{1-\bar{z_0}z} $ takes $z_0 \mapsto 0$. Where
must $f(z_1)$ be? Wherever it is, we can now measure its distance
to the origin and clear some fractions to get the formula
\begin{eqnarray*}
d_H(z_0,z_1) &=& \log( \frac{|1-\bar{z_0}z_1| + |z_1 - z_0|}
{|1-\bar{z_0}z_1| - |z_1 - z_0| }) \\
\end{eqnarray*}
\end{eqnarray*}
\begin{eqnarray*}
\end{eqnarray*}
 \section{Motivation}
In this lesson we apply the algebraic tools we have studies to geometrical
problems. We compare the algebraic proofs to their geometrical cousins.
Sometimes the one, sometimes the other kind of proof is easier. Both are
instructive.
\section{Verifying Euclid's first postulate}
We give both kind of proof of the verification that two Points in the
non-Euclidean plane are line on a unique Line. (Note the capitals).
\subsection{Geometric proof}
The two Points are modelled by two points, $p,q$ in the Poincare disk.
We need a circline through $p,q$ perpendicular to the unit circle.
If the two points lie on a diameter, we're done, the diameter is the
Line they lie on. If they do not, then we need a circle through them,
which is also perpendicular to the unit circle. Here is a construction
with ruler and compass.
\begin{itemize}
\item The center of this circle must be on the perpendicular bisectore of
any two points on the circel. So far we know about only two of them. So
construct the perpendicular bisector $\ell_{12}$ of the $segment(p,q)$.
\item We know such circles are symmetric with respect to the unit circle, so
we next find the symmetric point $q*=\frac{1}{\bar{q}}$ geometrically with
Thales' construction: $\ell_{q3}$ perpendicular to $\ell_{Oq}$ and
$\ell_{34}$ perpendicular to $\ell_{q3}$ meeting $\ell_{Oq}$ at $q*$.
\item The perpendicular bisector $\ell_{56}$ to $segment(q,4)$ meets the
other bisecor at the center $7$ of the required circle.
\item The portion inside the disk is the desired $L_{pq}$.
\end{itemize}
\subsection{Algebraic proof}
On W13 we discovered the equation
\begin{eqnarray*}
z\bar{z} + \mu \bar{z} + \bar{\mu}z + 1 &=& 0 \\
|z|^2 + \Re(\mu \bar{z}) + 1 &=& 0 \\
\end{eqnarray*}
of all circles perpendicular to the unit circle, and that it is
centered at $-\mu$ (outside the unit circle), with radius-squared
equal to $|\mu|^2-1$. But all we really need to do is find the
parameter $\mu$ by substituting the two given points into the equation.
Suppose $p = x_1 + iy_1, q= x_2 + iy_2 $, then solve the two linear equation:
\begin{eqnarray*}
|z_1|^2 + \mu_x x_1 + \mu_y y_1 + 1 &=& 0 \\
|z_2|^2 + \mu_x x_2 + \mu_y y_2 + 1 &=& 0 \\
\end{eqnarray*}
for the two unknowns $\mu_x + i \mu_y = \mu$.
\subsection{Comment}
Which of these two proofs do you find the easier? Depends, if you want to
avoid learning some complex number geometry, the geometrical one is clearer.
But complex number geometry is much more versatile, since it solves other
problems too.
\section{Hyperbolic distance}
We saw why $d_H(z_0, z_1) = | \log CR(z_0,\omega_0, z_1, \omega_1)| $ was
good choice for the distance function. (I hope you can answer that now,
and it is in your journal.!) Unfortunately, for the purpose of building
the Geometry Explorer, this is computationally expensive, because it
requires finding the omega-points (on the unit circle)
of the Line through the two points. In Exercise 8.2.13, Hvidsten tells
you to compute formula which depends only on the two given points. The
lemma for this is Proposition 8.14, for which we give the followig proof:
\subsection{ Distance from the origin}
Hyperbolic geometry has no preferred points, every point is equal! But
in the Poincare model this is definitely not the case. The origin of
the disk, which an ordinary Point, is a very special point in the model.
Similarly for diameters, especially the one on the real axis. Since
hyperbolic distance is based on cross ratios, and cross ratios are
invariant under Moebius transformations, inparticular on the isometries,
we can measure distances between Points by moving their Lines into a
special position using an isometry.
To compute $d_H(0,z)$ you can either calculate
$CR(0,-\frac{z}{|z|},z,\frac{z}{|z|})$ directly because it was easy to
find the omega points for Lines that are diameters. Or, we can be clever.
Rotating the entire disk by $z \mapsto e^{-i\theta}z = |z|$, where
$\theta = \arg(z)$, is an isometry, which takes $z$ to $r=|z|$. But
now $CR(0, -1, r, 1) = \frac{1-r}{1+r} <1$ , so the distance is
$d_H(0,r) = - \log\frac{1-r}{1+r}= \log\frac{1+r}{1-r}$ as claimed. Done.
\subsection{General case}
The trick is to reduce the general case (Exercise 8.2.13) to the
particular case (Proposition 8.14). The hyperbolic translation
$ f(z) = \frac{z-z_0}{1-\bar{z_0}z} $ takes $z_0 \mapsto 0$. Where
must $f(z_1)$ be? Wherever it is, we can now measure its distance
to the origin and clear some fractions to get the formula
\begin{eqnarray*}
d_H(z_0,z_1) &=& \log( \frac{|1-\bar{z_0}z_1| + |z_1 - z_0|}
{|1-\bar{z_0}z_1| - |z_1 - z_0| }) \\
\end{eqnarray*}
\end{eqnarray*}
\begin{eqnarray*}
\end{eqnarray*}
\section{Motivation}
In this lesson we apply the algebraic tools we have studies to geometrical
problems. We compare the algebraic proofs to their geometrical cousins.
Sometimes the one, sometimes the other kind of proof is easier. Both are
instructive.
\section{Verifying Euclid's first postulate}
We give both kind of proof of the verification that two Points in the
non-Euclidean plane are line on a unique Line. (Note the capitals).
\subsection{Geometric proof}
The two Points are modelled by two points, $p,q$ in the Poincare disk.
We need a circline through $p,q$ perpendicular to the unit circle.
If the two points lie on a diameter, we're done, the diameter is the
Line they lie on. If they do not, then we need a circle through them,
which is also perpendicular to the unit circle. Here is a construction
with ruler and compass.
\begin{itemize}
\item The center of this circle must be on the perpendicular bisectore of
any two points on the circel. So far we know about only two of them. So
construct the perpendicular bisector $\ell_{12}$ of the $segment(p,q)$.
\item We know such circles are symmetric with respect to the unit circle, so
we next find the symmetric point $q*=\frac{1}{\bar{q}}$ geometrically with
Thales' construction: $\ell_{q3}$ perpendicular to $\ell_{Oq}$ and
$\ell_{34}$ perpendicular to $\ell_{q3}$ meeting $\ell_{Oq}$ at $q*$.
\item The perpendicular bisector $\ell_{56}$ to $segment(q,4)$ meets the
other bisecor at the center $7$ of the required circle.
\item The portion inside the disk is the desired $L_{pq}$.
\end{itemize}
\subsection{Algebraic proof}
On W13 we discovered the equation
\begin{eqnarray*}
z\bar{z} + \mu \bar{z} + \bar{\mu}z + 1 &=& 0 \\
|z|^2 + \Re(\mu \bar{z}) + 1 &=& 0 \\
\end{eqnarray*}
of all circles perpendicular to the unit circle, and that it is
centered at $-\mu$ (outside the unit circle), with radius-squared
equal to $|\mu|^2-1$. But all we really need to do is find the
parameter $\mu$ by substituting the two given points into the equation.
Suppose $p = x_1 + iy_1, q= x_2 + iy_2 $, then solve the two linear equation:
\begin{eqnarray*}
|z_1|^2 + \mu_x x_1 + \mu_y y_1 + 1 &=& 0 \\
|z_2|^2 + \mu_x x_2 + \mu_y y_2 + 1 &=& 0 \\
\end{eqnarray*}
for the two unknowns $\mu_x + i \mu_y = \mu$.
\subsection{Comment}
Which of these two proofs do you find the easier? Depends, if you want to
avoid learning some complex number geometry, the geometrical one is clearer.
But complex number geometry is much more versatile, since it solves other
problems too.
\section{Hyperbolic distance}
We saw why $d_H(z_0, z_1) = | \log CR(z_0,\omega_0, z_1, \omega_1)| $ was
good choice for the distance function. (I hope you can answer that now,
and it is in your journal.!) Unfortunately, for the purpose of building
the Geometry Explorer, this is computationally expensive, because it
requires finding the omega-points (on the unit circle)
of the Line through the two points. In Exercise 8.2.13, Hvidsten tells
you to compute formula which depends only on the two given points. The
lemma for this is Proposition 8.14, for which we give the followig proof:
\subsection{ Distance from the origin}
Hyperbolic geometry has no preferred points, every point is equal! But
in the Poincare model this is definitely not the case. The origin of
the disk, which an ordinary Point, is a very special point in the model.
Similarly for diameters, especially the one on the real axis. Since
hyperbolic distance is based on cross ratios, and cross ratios are
invariant under Moebius transformations, inparticular on the isometries,
we can measure distances between Points by moving their Lines into a
special position using an isometry.
To compute $d_H(0,z)$ you can either calculate
$CR(0,-\frac{z}{|z|},z,\frac{z}{|z|})$ directly because it was easy to
find the omega points for Lines that are diameters. Or, we can be clever.
Rotating the entire disk by $z \mapsto e^{-i\theta}z = |z|$, where
$\theta = \arg(z)$, is an isometry, which takes $z$ to $r=|z|$. But
now $CR(0, -1, r, 1) = \frac{1-r}{1+r} <1$ , so the distance is
$d_H(0,r) = - \log\frac{1-r}{1+r}= \log\frac{1+r}{1-r}$ as claimed. Done.
\subsection{General case}
The trick is to reduce the general case (Exercise 8.2.13) to the
particular case (Proposition 8.14). The hyperbolic translation
$ f(z) = \frac{z-z_0}{1-\bar{z_0}z} $ takes $z_0 \mapsto 0$. Where
must $f(z_1)$ be? Wherever it is, we can now measure its distance
to the origin and clear some fractions to get the formula
\begin{eqnarray*}
d_H(z_0,z_1) &=& \log( \frac{|1-\bar{z_0}z_1| + |z_1 - z_0|}
{|1-\bar{z_0}z_1| - |z_1 - z_0| }) \\
\end{eqnarray*}
\end{eqnarray*}
\begin{eqnarray*}
\end{eqnarray*}