Last update 21apr22
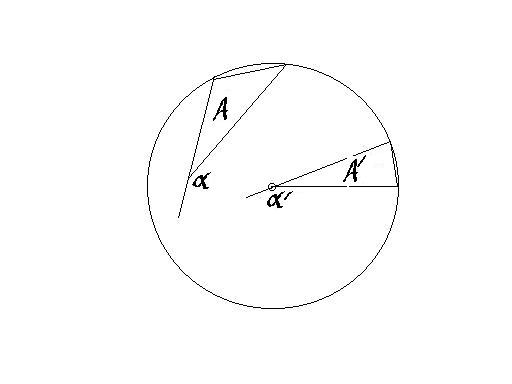 Consider an arbitrary monangle $A$. A hyperbolic isometry can be found to
move its vertex to the origin of the Klein model so that one leg of the
angle lies along the x-axis, and the other leg points into the upper
half-plane. The third side of this new monangle, $A'$, connects the two
ideal points on the boundary. For a given angle, there only one such standard
monangle $A'$. By transitivity of congruence then, every other monangle with
the same angle as $A$ has, is also congruent to $A'$.
For nulangles, we can drop the altitude from one of its sides to the opposite
side, dividing the nulangle into two right monangles. This construction depends on knowing the perpendiculars in whichever model we want to work with here.
Next, we can either apply the previous idea, moving the nulangle $B$ to a
standard position on horizontal diameter of the Klein (or Poincare) disk. The
altitude necessarily lands on the vertical radius, and so there is no choice
about the standard nulangle.
A nicer way is to apply the previous result for monangles directly in the
classical style. Take any two nulangles. Dissect each by an altitude and
note that the four right-angled monangles are all congruent. Done!
Dissection will continue to work for similar biangles, except now
pick one of the equal angles in the two biangles, and exend the finite
side past the other angle to infinity and comlete congruent monangles.
The third side, though it doesn't need to be an altitude, dissects the monangle
into another monangle and the original biangle. Done!
We leave the proof of AAA congruence for 3-angled triangles to the reader.
\subsection{Measuring Monangles by their Exterior Angle}
Consider an arbitrary monangle $A$. A hyperbolic isometry can be found to
move its vertex to the origin of the Klein model so that one leg of the
angle lies along the x-axis, and the other leg points into the upper
half-plane. The third side of this new monangle, $A'$, connects the two
ideal points on the boundary. For a given angle, there only one such standard
monangle $A'$. By transitivity of congruence then, every other monangle with
the same angle as $A$ has, is also congruent to $A'$.
For nulangles, we can drop the altitude from one of its sides to the opposite
side, dividing the nulangle into two right monangles. This construction depends on knowing the perpendiculars in whichever model we want to work with here.
Next, we can either apply the previous idea, moving the nulangle $B$ to a
standard position on horizontal diameter of the Klein (or Poincare) disk. The
altitude necessarily lands on the vertical radius, and so there is no choice
about the standard nulangle.
A nicer way is to apply the previous result for monangles directly in the
classical style. Take any two nulangles. Dissect each by an altitude and
note that the four right-angled monangles are all congruent. Done!
Dissection will continue to work for similar biangles, except now
pick one of the equal angles in the two biangles, and exend the finite
side past the other angle to infinity and comlete congruent monangles.
The third side, though it doesn't need to be an altitude, dissects the monangle
into another monangle and the original biangle. Done!
We leave the proof of AAA congruence for 3-angled triangles to the reader.
\subsection{Measuring Monangles by their Exterior Angle}
 Measuring monangles is interesting because we will use a form of
continuity you are familiar with from the MA347 prerequisite on
the density of rational numbers in an interval, which we will
refer to as the \textit{inch-worm principle}.
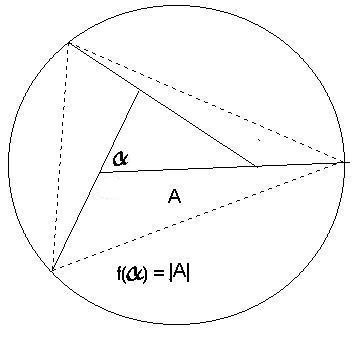
\textbf{Definition: } For a monangle $A$ with sole \textbf{exterior angle}
$\alpha$ let $f(\alpha) = |A|$, the area of the monangle.
Since all monangles with the same interior angle, $\pi -\alpha$,
are congruent, this is truly a function of the angle
(not the particular monangle).
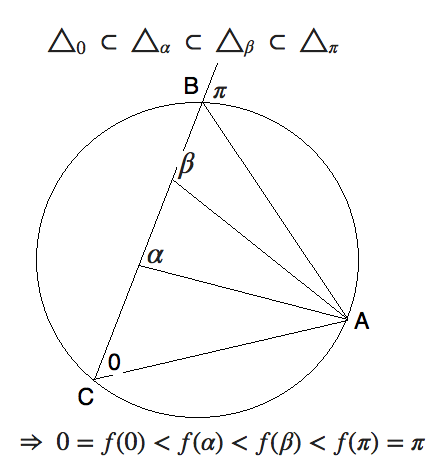
From the figure we see how $f(\alpha)$ is an increasing function from
$0$ to $\pi$. Assuming that it is a continuous function, we shall next how
that it is a linear function.
Recall that we need prove two properties of a function $f(\alpha)$
to make it linear
\begin{itemize}
\item $f(\alpha + \beta) = f(\alpha) + f(\beta)$ (Additivity).
\item For any real $t$, $f(t\alpha) = tf(\alpha)$ (Scalability)$
\end{itemize}
\textbf{Additivity Theorem:}
If ${0 < \{\alpha, \beta\} < \alpha + \beta < \pi }$ then
${ f(\alpha + \beta) = f(\alpha) + f(\beta) }$.
Measuring monangles is interesting because we will use a form of
continuity you are familiar with from the MA347 prerequisite on
the density of rational numbers in an interval, which we will
refer to as the \textit{inch-worm principle}.
\textbf{Definition: } For a monangle $A$ with sole \textbf{exterior angle}
$\alpha$ let $f(\alpha) = |A|$, the area of the monangle.
Since all monangles with the same interior angle, $\pi -\alpha$,
are congruent, this is truly a function of the angle
(not the particular monangle).
From the figure we see how $f(\alpha)$ is an increasing function from
$0$ to $\pi$. Assuming that it is a continuous function, we shall next how
that it is a linear function.
Recall that we need prove two properties of a function $f(\alpha)$
to make it linear
\begin{itemize}
\item $f(\alpha + \beta) = f(\alpha) + f(\beta)$ (Additivity).
\item For any real $t$, $f(t\alpha) = tf(\alpha)$ (Scalability)$
\end{itemize}
\textbf{Additivity Theorem:}
If ${0 < \{\alpha, \beta\} < \alpha + \beta < \pi }$ then
${ f(\alpha + \beta) = f(\alpha) + f(\beta) }$.
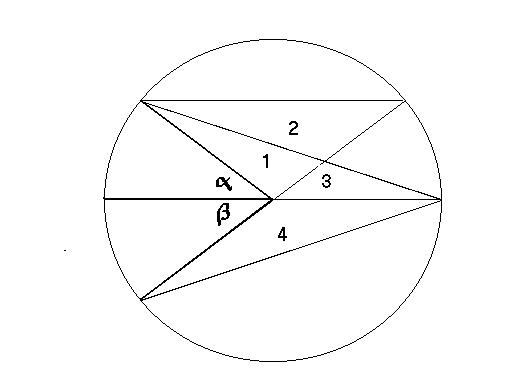 \txtbf{Proof:}
In the Klein model, put both angles at its center,
one above and one below a diameter. We draw the picture when
both angles are acute. You draw the picture and give the
argument when one of the angles is obtuse. Why can't both
angles be obtuse?
Draw additional lines forming four triangles, which we label
${1,2,3,4}$. Their areas will be denotes by ${|1|, |2|}$ etc.
Observe that
\begin{eqnarray*}
f(\beta) &=& |4| \quad \mbox{ by definition } \\
f(\alpha) &=& |1| + |3| \quad
\mbox{ look who } \alpha \mbox{ is exterior to } \\
f(\alpha + \beta) &=& |1| + |2| \\
|2| &=& |3| + |4| \quad \mbox{by VAT and proposition 3}\\
\end{eqnarray*}
Collecting the algebra we have
\[f(\alpha + \beta) = |1| + |2|
= |1| + (|3| + |4|) = ( |1| + |3| ) + |4| = f(\alpha)+f(\beta) \]
You should do the obtuse case in your journal.
The additivity is almost the same as linearity. For any rational
multiple of an angle (so long as its less than $\pi$) we have
\[ d\; f(\frac{n}{d}\theta) = f(n\theta) = nf(\theta)
\Rightarrow f(\frac{n}{d}\theta) =\frac{n}{d}f(\theta).\]
If we are willing to accept that $f$ is also continuous, we
get that $f(t\theta)=tf(\theta)}$ and we have completed
the proof the linearity.
Finally, to show that $f(\alpha) = \alpha$ we need only to
decide the constant representing the area of an ideal triangle
(nulangle) for the only linear function $f(\alpha)$ that rises from
$0$ to $f(\pi)$ must be proportional to its argument, as it goes
from $0$ to $\pi$. The (negative of the) proportionality constant is
called the \textit{curvature} of the non-Euclidean plane. Along with
Gauss, we choose that to be $-1$.
\section{Finishing the Proof of Gauss' Theorem}
\txtbf{Proof:}
In the Klein model, put both angles at its center,
one above and one below a diameter. We draw the picture when
both angles are acute. You draw the picture and give the
argument when one of the angles is obtuse. Why can't both
angles be obtuse?
Draw additional lines forming four triangles, which we label
${1,2,3,4}$. Their areas will be denotes by ${|1|, |2|}$ etc.
Observe that
\begin{eqnarray*}
f(\beta) &=& |4| \quad \mbox{ by definition } \\
f(\alpha) &=& |1| + |3| \quad
\mbox{ look who } \alpha \mbox{ is exterior to } \\
f(\alpha + \beta) &=& |1| + |2| \\
|2| &=& |3| + |4| \quad \mbox{by VAT and proposition 3}\\
\end{eqnarray*}
Collecting the algebra we have
\[f(\alpha + \beta) = |1| + |2|
= |1| + (|3| + |4|) = ( |1| + |3| ) + |4| = f(\alpha)+f(\beta) \]
You should do the obtuse case in your journal.
The additivity is almost the same as linearity. For any rational
multiple of an angle (so long as its less than $\pi$) we have
\[ d\; f(\frac{n}{d}\theta) = f(n\theta) = nf(\theta)
\Rightarrow f(\frac{n}{d}\theta) =\frac{n}{d}f(\theta).\]
If we are willing to accept that $f$ is also continuous, we
get that $f(t\theta)=tf(\theta)}$ and we have completed
the proof the linearity.
Finally, to show that $f(\alpha) = \alpha$ we need only to
decide the constant representing the area of an ideal triangle
(nulangle) for the only linear function $f(\alpha)$ that rises from
$0$ to $f(\pi)$ must be proportional to its argument, as it goes
from $0$ to $\pi$. The (negative of the) proportionality constant is
called the \textit{curvature} of the non-Euclidean plane. Along with
Gauss, we choose that to be $-1$.
\section{Finishing the Proof of Gauss' Theorem}
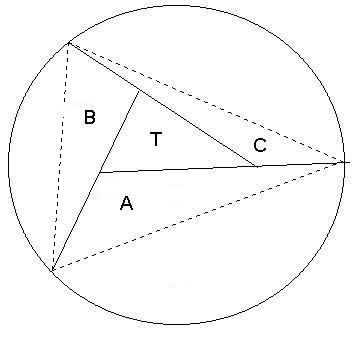
 Consider a hyperbolic triangle $T$ with angles $\alpha, \beta, \gamma $
Extend the sides
pinwheel-fashion. In the Klein model this is easy to do. These extended sides
\textit{end at infinity} and surround our triangle inside an an
ideal triangle $I$, which has been dissected into three monangles of areas
$\alpha = |A|, \beta = |B|, \gamma = |C| $ leaving the original triangle.
\begin{eqnarray*}
I &=& T + A + B + C \\
\pi &=& |T| + f(\alpha) + f(\beta) + f(\gamma) \\
&=& |T| + (\alpha + \beta+ \gamma) \\
|T| &=& ( \pi - \alpha - \beta - \gamma) = \mbox{ angular defect of } T .
\end{eqnarray*}
\end{document}
Consider a hyperbolic triangle $T$ with angles $\alpha, \beta, \gamma $
Extend the sides
pinwheel-fashion. In the Klein model this is easy to do. These extended sides
\textit{end at infinity} and surround our triangle inside an an
ideal triangle $I$, which has been dissected into three monangles of areas
$\alpha = |A|, \beta = |B|, \gamma = |C| $ leaving the original triangle.
\begin{eqnarray*}
I &=& T + A + B + C \\
\pi &=& |T| + f(\alpha) + f(\beta) + f(\gamma) \\
&=& |T| + (\alpha + \beta+ \gamma) \\
|T| &=& ( \pi - \alpha - \beta - \gamma) = \mbox{ angular defect of } T .
\end{eqnarray*}
\end{document}
Non-EuclideanArea and Gauss' Theorem (Part 2)
\textit{(C) 2004, 2015 George K. Francis, Mathematics Department, University of Illinois} \begin{document} \maketitle \section{Introduction} We complete the lesson that non-Euclidean area is entirely determined by the angles of a triangle. Recall that absolute geometry has SSS congruence. We also saw that AAA is not a congruence in Euclidean geometry. But AAA does establish similarity. Since there is no similarity in hyperbolic geometry, AAA should be a congruence relation there. For instance, since ideal triangles (nulangles) have three pairs of asymptotic sides, each meeting in a zero-angle, should be congruent. Right angles being congruent, as Euclid observed, should mean that all nulangles whose single angle is a right angle, should be congruent too, and so forth. And they are, as we now show. \section{Congruences are Angle Dependent} In the first half of this lesson, we saw that all triangles, ideal or not, have finite area. In showing that AAA-congruence is true in non-Euclidean geometry, there are two issues to consider separately, at first. \begin{itemize} \item Its angles \textit{determines} a triangle, ideal or not, up to congruence. \item The area of a triangle is measured by its \textit{angle defect}. \end{itemize} These two are not identical concepts. The first feature is derived from using the hyperbolic isometry group to move similar triangles into a standard position. This is essentially how Euclid meant to establish congruence by superposition of two figures. With Klein's Erlanged Program we can make the method of superposition precise. The second feature has an interesting, classical proof for the case of monangles, except that we invoke \textit{continuity}, which Euclid did not understand. \subsection{Congruence of Triangles with Similar Angles}} We begin with monangles. Consider an arbitrary monangle $A$. A hyperbolic isometry can be found to
move its vertex to the origin of the Klein model so that one leg of the
angle lies along the x-axis, and the other leg points into the upper
half-plane. The third side of this new monangle, $A'$, connects the two
ideal points on the boundary. For a given angle, there only one such standard
monangle $A'$. By transitivity of congruence then, every other monangle with
the same angle as $A$ has, is also congruent to $A'$.
For nulangles, we can drop the altitude from one of its sides to the opposite
side, dividing the nulangle into two right monangles. This construction depends on knowing the perpendiculars in whichever model we want to work with here.
Next, we can either apply the previous idea, moving the nulangle $B$ to a
standard position on horizontal diameter of the Klein (or Poincare) disk. The
altitude necessarily lands on the vertical radius, and so there is no choice
about the standard nulangle.
A nicer way is to apply the previous result for monangles directly in the
classical style. Take any two nulangles. Dissect each by an altitude and
note that the four right-angled monangles are all congruent. Done!
Dissection will continue to work for similar biangles, except now
pick one of the equal angles in the two biangles, and exend the finite
side past the other angle to infinity and comlete congruent monangles.
The third side, though it doesn't need to be an altitude, dissects the monangle
into another monangle and the original biangle. Done!
We leave the proof of AAA congruence for 3-angled triangles to the reader.
\subsection{Measuring Monangles by their Exterior Angle}
Consider an arbitrary monangle $A$. A hyperbolic isometry can be found to
move its vertex to the origin of the Klein model so that one leg of the
angle lies along the x-axis, and the other leg points into the upper
half-plane. The third side of this new monangle, $A'$, connects the two
ideal points on the boundary. For a given angle, there only one such standard
monangle $A'$. By transitivity of congruence then, every other monangle with
the same angle as $A$ has, is also congruent to $A'$.
For nulangles, we can drop the altitude from one of its sides to the opposite
side, dividing the nulangle into two right monangles. This construction depends on knowing the perpendiculars in whichever model we want to work with here.
Next, we can either apply the previous idea, moving the nulangle $B$ to a
standard position on horizontal diameter of the Klein (or Poincare) disk. The
altitude necessarily lands on the vertical radius, and so there is no choice
about the standard nulangle.
A nicer way is to apply the previous result for monangles directly in the
classical style. Take any two nulangles. Dissect each by an altitude and
note that the four right-angled monangles are all congruent. Done!
Dissection will continue to work for similar biangles, except now
pick one of the equal angles in the two biangles, and exend the finite
side past the other angle to infinity and comlete congruent monangles.
The third side, though it doesn't need to be an altitude, dissects the monangle
into another monangle and the original biangle. Done!
We leave the proof of AAA congruence for 3-angled triangles to the reader.
\subsection{Measuring Monangles by their Exterior Angle}
 Measuring monangles is interesting because we will use a form of
continuity you are familiar with from the MA347 prerequisite on
the density of rational numbers in an interval, which we will
refer to as the \textit{inch-worm principle}.
\textbf{Definition: } For a monangle $A$ with sole \textbf{exterior angle}
$\alpha$ let $f(\alpha) = |A|$, the area of the monangle.
Since all monangles with the same interior angle, $\pi -\alpha$,
are congruent, this is truly a function of the angle
(not the particular monangle).
From the figure we see how $f(\alpha)$ is an increasing function from
$0$ to $\pi$. Assuming that it is a continuous function, we shall next how
that it is a linear function.
Recall that we need prove two properties of a function $f(\alpha)$
to make it linear
\begin{itemize}
\item $f(\alpha + \beta) = f(\alpha) + f(\beta)$ (Additivity).
\item For any real $t$, $f(t\alpha) = tf(\alpha)$ (Scalability)$
\end{itemize}
\textbf{Additivity Theorem:}
If ${0 < \{\alpha, \beta\} < \alpha + \beta < \pi }$ then
${ f(\alpha + \beta) = f(\alpha) + f(\beta) }$.
Measuring monangles is interesting because we will use a form of
continuity you are familiar with from the MA347 prerequisite on
the density of rational numbers in an interval, which we will
refer to as the \textit{inch-worm principle}.
\textbf{Definition: } For a monangle $A$ with sole \textbf{exterior angle}
$\alpha$ let $f(\alpha) = |A|$, the area of the monangle.
Since all monangles with the same interior angle, $\pi -\alpha$,
are congruent, this is truly a function of the angle
(not the particular monangle).
From the figure we see how $f(\alpha)$ is an increasing function from
$0$ to $\pi$. Assuming that it is a continuous function, we shall next how
that it is a linear function.
Recall that we need prove two properties of a function $f(\alpha)$
to make it linear
\begin{itemize}
\item $f(\alpha + \beta) = f(\alpha) + f(\beta)$ (Additivity).
\item For any real $t$, $f(t\alpha) = tf(\alpha)$ (Scalability)$
\end{itemize}
\textbf{Additivity Theorem:}
If ${0 < \{\alpha, \beta\} < \alpha + \beta < \pi }$ then
${ f(\alpha + \beta) = f(\alpha) + f(\beta) }$.
 \txtbf{Proof:}
In the Klein model, put both angles at its center,
one above and one below a diameter. We draw the picture when
both angles are acute. You draw the picture and give the
argument when one of the angles is obtuse. Why can't both
angles be obtuse?
Draw additional lines forming four triangles, which we label
${1,2,3,4}$. Their areas will be denotes by ${|1|, |2|}$ etc.
Observe that
\begin{eqnarray*}
f(\beta) &=& |4| \quad \mbox{ by definition } \\
f(\alpha) &=& |1| + |3| \quad
\mbox{ look who } \alpha \mbox{ is exterior to } \\
f(\alpha + \beta) &=& |1| + |2| \\
|2| &=& |3| + |4| \quad \mbox{by VAT and proposition 3}\\
\end{eqnarray*}
Collecting the algebra we have
\[f(\alpha + \beta) = |1| + |2|
= |1| + (|3| + |4|) = ( |1| + |3| ) + |4| = f(\alpha)+f(\beta) \]
You should do the obtuse case in your journal.
The additivity is almost the same as linearity. For any rational
multiple of an angle (so long as its less than $\pi$) we have
\[ d\; f(\frac{n}{d}\theta) = f(n\theta) = nf(\theta)
\Rightarrow f(\frac{n}{d}\theta) =\frac{n}{d}f(\theta).\]
If we are willing to accept that $f$ is also continuous, we
get that $f(t\theta)=tf(\theta)}$ and we have completed
the proof the linearity.
Finally, to show that $f(\alpha) = \alpha$ we need only to
decide the constant representing the area of an ideal triangle
(nulangle) for the only linear function $f(\alpha)$ that rises from
$0$ to $f(\pi)$ must be proportional to its argument, as it goes
from $0$ to $\pi$. The (negative of the) proportionality constant is
called the \textit{curvature} of the non-Euclidean plane. Along with
Gauss, we choose that to be $-1$.
\section{Finishing the Proof of Gauss' Theorem}
\txtbf{Proof:}
In the Klein model, put both angles at its center,
one above and one below a diameter. We draw the picture when
both angles are acute. You draw the picture and give the
argument when one of the angles is obtuse. Why can't both
angles be obtuse?
Draw additional lines forming four triangles, which we label
${1,2,3,4}$. Their areas will be denotes by ${|1|, |2|}$ etc.
Observe that
\begin{eqnarray*}
f(\beta) &=& |4| \quad \mbox{ by definition } \\
f(\alpha) &=& |1| + |3| \quad
\mbox{ look who } \alpha \mbox{ is exterior to } \\
f(\alpha + \beta) &=& |1| + |2| \\
|2| &=& |3| + |4| \quad \mbox{by VAT and proposition 3}\\
\end{eqnarray*}
Collecting the algebra we have
\[f(\alpha + \beta) = |1| + |2|
= |1| + (|3| + |4|) = ( |1| + |3| ) + |4| = f(\alpha)+f(\beta) \]
You should do the obtuse case in your journal.
The additivity is almost the same as linearity. For any rational
multiple of an angle (so long as its less than $\pi$) we have
\[ d\; f(\frac{n}{d}\theta) = f(n\theta) = nf(\theta)
\Rightarrow f(\frac{n}{d}\theta) =\frac{n}{d}f(\theta).\]
If we are willing to accept that $f$ is also continuous, we
get that $f(t\theta)=tf(\theta)}$ and we have completed
the proof the linearity.
Finally, to show that $f(\alpha) = \alpha$ we need only to
decide the constant representing the area of an ideal triangle
(nulangle) for the only linear function $f(\alpha)$ that rises from
$0$ to $f(\pi)$ must be proportional to its argument, as it goes
from $0$ to $\pi$. The (negative of the) proportionality constant is
called the \textit{curvature} of the non-Euclidean plane. Along with
Gauss, we choose that to be $-1$.
\section{Finishing the Proof of Gauss' Theorem}

 Consider a hyperbolic triangle $T$ with angles $\alpha, \beta, \gamma $
Extend the sides
pinwheel-fashion. In the Klein model this is easy to do. These extended sides
\textit{end at infinity} and surround our triangle inside an an
ideal triangle $I$, which has been dissected into three monangles of areas
$\alpha = |A|, \beta = |B|, \gamma = |C| $ leaving the original triangle.
\begin{eqnarray*}
I &=& T + A + B + C \\
\pi &=& |T| + f(\alpha) + f(\beta) + f(\gamma) \\
&=& |T| + (\alpha + \beta+ \gamma) \\
|T| &=& ( \pi - \alpha - \beta - \gamma) = \mbox{ angular defect of } T .
\end{eqnarray*}
\end{document}
Consider a hyperbolic triangle $T$ with angles $\alpha, \beta, \gamma $
Extend the sides
pinwheel-fashion. In the Klein model this is easy to do. These extended sides
\textit{end at infinity} and surround our triangle inside an an
ideal triangle $I$, which has been dissected into three monangles of areas
$\alpha = |A|, \beta = |B|, \gamma = |C| $ leaving the original triangle.
\begin{eqnarray*}
I &=& T + A + B + C \\
\pi &=& |T| + f(\alpha) + f(\beta) + f(\gamma) \\
&=& |T| + (\alpha + \beta+ \gamma) \\
|T| &=& ( \pi - \alpha - \beta - \gamma) = \mbox{ angular defect of } T .
\end{eqnarray*}
\end{document}