%\title{Lesson on Area and Gauss'
%Theorem\footnote{Revision of {\it Post-Euclidean
%Geometry: Class Notes and Workbook}, UpClose Printing \& Copies,
%Champaign, IL 1995}
%}
%\author{George Francis\footnote{(C) 2004, Prof. George K. Francis, Mathematics
%Department, University of Illinois.}}
Last update 21apr15.
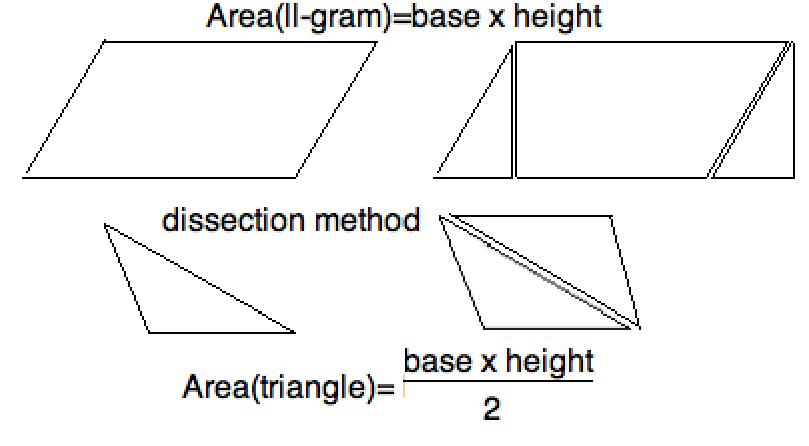
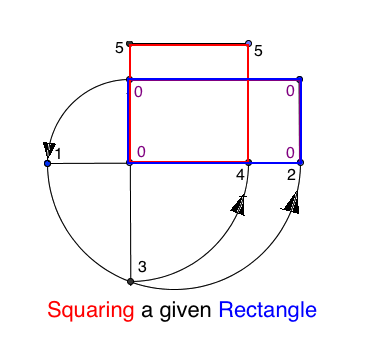 This figure reminds you how to deduce the area of a triangle
by dissection from the area of a rectangle. The Greeks, who
preferred beauty over practicality, also knew how to relate
the area $ab$ of a rectangle to that of a square of side $s$.
Recall their \textit{geometric mean}, $s = \sqrt{ab}$ was
constructible. Indeed, geometers like Newton still referred to finding
the area under a curve as \textit{squaring the figure}. (Finding the
length of a curve, which Newton also used his calculus for, was called
\textig{rectifying the curve} since, to the Greeks, it meant constructing
a segment of that length.
this lesson.
\section{On the Sphere }
On the sphere, triangles have an angle sum greater than $\pi$.
Experimenting with a dynamical geometry construction package, such as
such as GEX2.0, or with some spherical trigonometry leads you to discover
the \textin{angular excess theorem} for spherical geometry. One
example can be done in your head. Imagine walking west on the
equator and making a right turn, heading due north. At the north
pole make another right turn, heading south. At the equator you
will have made a rectangular triangle. Compared to a Euclidean
triangle, it has one too many right angles. It has angular excess of
$\pi/2$.
\section{On the Hyperbolic Plane}
Recall the construction that showed that the Euclidean
\textit{Exterior Angle Theorem} (EXAT) fails to be true in the
Klein model of $\mathbb{H}^2$. The amount by which it fails to be true
is also the angular defect, because the exterior angle opposite two
interior angles $\alpha, \beta$ is $c=\pi-\gamma$. Hence
\[c - (\alpha + \beta) = \pi -(\alpha+\beta+\gamma) = \mbox{defect} \]
This too may be determined experimentally with Hvidsten's GEX2.0
or Joel Castellano's \textit{NonEuclid}. The smaller the triangle,
the smaller the angular defect. And, as you moved the vertices
closer to the boundary unit circle of the Poincar'e disk, the defect
approached zero.
The method of dissection alone suffices to determine that angular defect,
like area, is \textit{additive}, in the sense that the angular defect of
of a triangle composed of the sum of two adjacent triangle is the sum of
their angular defects.
This figure reminds you how to deduce the area of a triangle
by dissection from the area of a rectangle. The Greeks, who
preferred beauty over practicality, also knew how to relate
the area $ab$ of a rectangle to that of a square of side $s$.
Recall their \textit{geometric mean}, $s = \sqrt{ab}$ was
constructible. Indeed, geometers like Newton still referred to finding
the area under a curve as \textit{squaring the figure}. (Finding the
length of a curve, which Newton also used his calculus for, was called
\textig{rectifying the curve} since, to the Greeks, it meant constructing
a segment of that length.
this lesson.
\section{On the Sphere }
On the sphere, triangles have an angle sum greater than $\pi$.
Experimenting with a dynamical geometry construction package, such as
such as GEX2.0, or with some spherical trigonometry leads you to discover
the \textin{angular excess theorem} for spherical geometry. One
example can be done in your head. Imagine walking west on the
equator and making a right turn, heading due north. At the north
pole make another right turn, heading south. At the equator you
will have made a rectangular triangle. Compared to a Euclidean
triangle, it has one too many right angles. It has angular excess of
$\pi/2$.
\section{On the Hyperbolic Plane}
Recall the construction that showed that the Euclidean
\textit{Exterior Angle Theorem} (EXAT) fails to be true in the
Klein model of $\mathbb{H}^2$. The amount by which it fails to be true
is also the angular defect, because the exterior angle opposite two
interior angles $\alpha, \beta$ is $c=\pi-\gamma$. Hence
\[c - (\alpha + \beta) = \pi -(\alpha+\beta+\gamma) = \mbox{defect} \]
This too may be determined experimentally with Hvidsten's GEX2.0
or Joel Castellano's \textit{NonEuclid}. The smaller the triangle,
the smaller the angular defect. And, as you moved the vertices
closer to the boundary unit circle of the Poincar'e disk, the defect
approached zero.
The method of dissection alone suffices to determine that angular defect,
like area, is \textit{additive}, in the sense that the angular defect of
of a triangle composed of the sum of two adjacent triangle is the sum of
their angular defects.
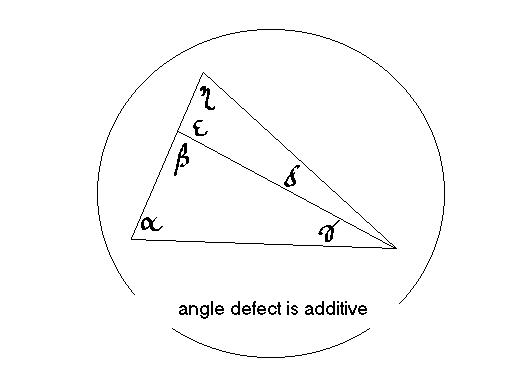 \textbf{Theorem:} The angle defect is additive.
\textbf{Proof:} We rewrite the angle defect of the sum of two triangles
formed by a Cevian of a third triangle.
\begin{eqnarray*}
\mbox{Defect of both}&=&\pi - (\alpha + (\gamma + \delta) + \eta ) \\
&=& (\pi - \alpha -\beta - \gamma) + \beta - \delta - \eta \\
&=& \mbox{left} + (\pi - \epsilon) -\delta - \eta \\
&=& \mbox{left} + (\pi - (\epsilon + \delta + \eta ) \\
&=& \mbox{left defect } + \mbox{ right defect}
\end{eqnarray*}
\section{Ideal Triangles}
Every triangle is a trilateral in that is is formed by three non-concurrent
lines. But the converse is not true, even in the Euclidean plane.
There, a trilateral could consists of two parallel rays attached to a line segment. That would be a \textit{bi-angle} because
it has only two proper angles.
\textbf{Theorem:} The angle defect is additive.
\textbf{Proof:} We rewrite the angle defect of the sum of two triangles
formed by a Cevian of a third triangle.
\begin{eqnarray*}
\mbox{Defect of both}&=&\pi - (\alpha + (\gamma + \delta) + \eta ) \\
&=& (\pi - \alpha -\beta - \gamma) + \beta - \delta - \eta \\
&=& \mbox{left} + (\pi - \epsilon) -\delta - \eta \\
&=& \mbox{left} + (\pi - (\epsilon + \delta + \eta ) \\
&=& \mbox{left defect } + \mbox{ right defect}
\end{eqnarray*}
\section{Ideal Triangles}
Every triangle is a trilateral in that is is formed by three non-concurrent
lines. But the converse is not true, even in the Euclidean plane.
There, a trilateral could consists of two parallel rays attached to a line segment. That would be a \textit{bi-angle} because
it has only two proper angles.
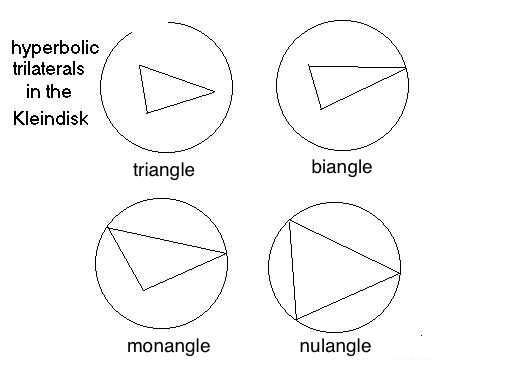 In $\mathbb{H}^2$ trilaterals come in four interesting kinds, look at the
Klein model. With three positive angles, it's an ordinary triangle.
With two angles, but with two lines \textit{asymptotically parallel}
(in the model the lines meet on the boundary), we'll call it a
\textit{biangle}. But now we can have \textit{monangles}, with but one
positive angle. The \textit{nulangles}, which have no positive angles, are
of special interest, and these are often called by their historical
name \textit{ideal triangles}. (Only the first and last terms are universal in
geometry, the others I made up.)
What is significant about two asymptotic lines is that they are parallel in
that they do not meet in a hyperbolic point, but they do not have a common
perpendicular. No parallel hyperbolic lines have two common perpendiculars,
for that would form a forbidden rectangle. How different matters are in
non-Euclidean geometry! Only triangles have finite area in the Euclidean plane. The region between two Euclidean parallels and a transversal has infinite area.
(In on the sphere there are no parallels at all, and everything, even the entire
spherical plane has finite area.)
Not so, and that is what we shall show first, in the hyperbolic plane. We shall
next prove the main lemma to Gauss's Theorem. The theorem states that all
ideal triangles (nulangles) are congruent and have finite area $\pi$.
This is appropriate because all three angles of a nulangle are zero, hence
the angular defect is $\pi$.
\section{Finite Area Lemma}
Here we show that all four kinds of hyperbolic triangles we defined above
have finite area. We begin with biangles where the construction and proof
is the easiest to understand. And then use the method of dissection to
dispose of the other three by using biangles to measure their area.
\textbf{Theorem: } Biangles Have Finite Areas.
In $\mathbb{H}^2$ trilaterals come in four interesting kinds, look at the
Klein model. With three positive angles, it's an ordinary triangle.
With two angles, but with two lines \textit{asymptotically parallel}
(in the model the lines meet on the boundary), we'll call it a
\textit{biangle}. But now we can have \textit{monangles}, with but one
positive angle. The \textit{nulangles}, which have no positive angles, are
of special interest, and these are often called by their historical
name \textit{ideal triangles}. (Only the first and last terms are universal in
geometry, the others I made up.)
What is significant about two asymptotic lines is that they are parallel in
that they do not meet in a hyperbolic point, but they do not have a common
perpendicular. No parallel hyperbolic lines have two common perpendiculars,
for that would form a forbidden rectangle. How different matters are in
non-Euclidean geometry! Only triangles have finite area in the Euclidean plane. The region between two Euclidean parallels and a transversal has infinite area.
(In on the sphere there are no parallels at all, and everything, even the entire
spherical plane has finite area.)
Not so, and that is what we shall show first, in the hyperbolic plane. We shall
next prove the main lemma to Gauss's Theorem. The theorem states that all
ideal triangles (nulangles) are congruent and have finite area $\pi$.
This is appropriate because all three angles of a nulangle are zero, hence
the angular defect is $\pi$.
\section{Finite Area Lemma}
Here we show that all four kinds of hyperbolic triangles we defined above
have finite area. We begin with biangles where the construction and proof
is the easiest to understand. And then use the method of dissection to
dispose of the other three by using biangles to measure their area.
\textbf{Theorem: } Biangles Have Finite Areas.
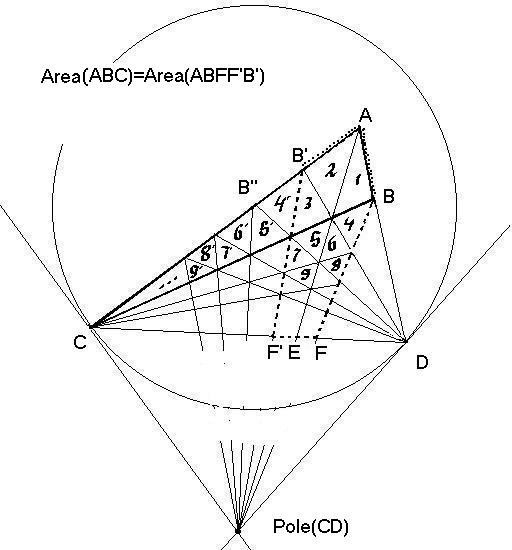 For the proof of the
\begin{itemize}
\item [Step 1:]
In the figure the biangle $\triangle ABC$ is given. We extend the side
between its two positive angles $AB$ to a ray $AD$ where $D$ is on the
unit circle.
\item [Step 2:]
Note that $D$ is not a hyperbolic point, and $\triangle$ is, in fact,
a monangle with one side an entire hyperbolic line $\ell_{CD}$.
We shall need the pole of secant $CD$ to drop hyperbolic perpendiculars.
\item [Step 3:]
There are, at this point only two finite points, $A,B$, to connect to this
pole. And the perpendiculars to them cross the polar, $\ell_{CD}$, at
the points $E,F$ respectively.
\end{itemize}
\subsection{Hyperbolic Reflections}
At this point we pause the proof to explain that we need the hyperbolic
isometries (congruence) of reflections across a line in the Klein model.
We have not defined these yet. Here we shall merely make the plausible
and continue.
For the proof of the
\begin{itemize}
\item [Step 1:]
In the figure the biangle $\triangle ABC$ is given. We extend the side
between its two positive angles $AB$ to a ray $AD$ where $D$ is on the
unit circle.
\item [Step 2:]
Note that $D$ is not a hyperbolic point, and $\triangle$ is, in fact,
a monangle with one side an entire hyperbolic line $\ell_{CD}$.
We shall need the pole of secant $CD$ to drop hyperbolic perpendiculars.
\item [Step 3:]
There are, at this point only two finite points, $A,B$, to connect to this
pole. And the perpendiculars to them cross the polar, $\ell_{CD}$, at
the points $E,F$ respectively.
\end{itemize}
\subsection{Hyperbolic Reflections}
At this point we pause the proof to explain that we need the hyperbolic
isometries (congruence) of reflections across a line in the Klein model.
We have not defined these yet. Here we shall merely make the plausible
and continue.
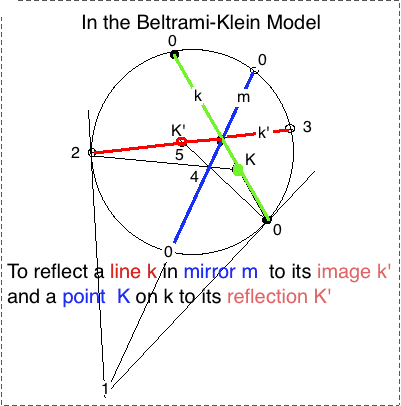 Recall that in the Euclidean plane, a reflection across a mirror line
entails moving every point on one side of the mirror to a point on the
other along a perpendicular and the same distance. In other words,
the mirror is the perpendicular bisector between a point and its reflection
in the mirror.
If we use our familiar Poincare disk model, we can define such a reflection
as follows. Suppose The mirror is the line $(PQ)$, use an isometry $h_{PQ}$
which takes it to the real-line by sending $P \mapsto 0$ and
"endpoints" $P',Q'$ of $(PQ)$ to $-1, +1$ . We can use crossratios to
define it implicitly thus:
\[ CR(h_{PQ}(z), -1,0,1)=CR(z,P',P,Q')$ \]
Note that, being an isometry, it also sends $Q \mapsto d_H(P,Q)$.
Reflections across the real axis, $w\mapsto \bar{w}$
is clearly a reflection which is expressed by taking the conjugate.
So \[\sigma_{PQ}(z) = h_{PQ}^{-1}(\bar{h_{PQ}(z)})\]
is the general reflection across $(PQ)$.
However, in the Klein Model there is a more constructive way of doing this
and we shall have a look at it later. Here we only need to know that
\textbf{K-reflection lemma:} Given a mirror line $m$ crossed by line $k$ with
point $K$ on it, the reflection proceeds in 5 steps as shown in the figure so
labelled.
\subsection{Completion of the Proof of Biangle Theorem}
\begin{itemize}
\item [Step 4:] Draw mirror $m_1 = (AE)$ and reflect $B \mapsto B'$.
\item [Step 5:] Since $m_1 \perp (CD) $ we have that
\begin{eqnarray*}
\sigma_1(CD) & = & (DC) \\
\sigma_1(A) & = & (A) \\
\sigma_1(CB)& = &(DB') \\
\sigma_1(PB)& = &(PB') \\
\sigma_1(\triangle_1)& = & \triangle_2\\
\triangle_1 & \cong & \triangle_2\\
\triangle_3 & \cong & \triangle_4\\
\end{eqnarray*}
\item [Step 6:] Since $m_1 \perp (CD) $ we have that
Note that 3 of these triangles are in two regions: the original
biangle $\triangle ABC$ and the pentagonal \textit{pentahouse}
$ABFF'B'$. But $\triangle_4$ is only in the pentahouse.
\item [Step 6:] A second mirror $m_2=(PB')$, with reflection $\sigma_2$
lets us find a congruent cousin to $\triangle _{4'}$, which is only inside
the biangle.
\begin{eqnarray*}
\triangle_3&=&\sigma_1(\triangle_4) \\
\triangle_{4'}&=&\sigma_2(\triangle_3) \\
\end{eqnarray*}
\item [Step 7:]
The strategy is now apparent. We have reflected $(CB)$ across
$(DB')$ to obtain $(DB'')=m_2$, the next mirror.
\item [Step 8:] Reflecting
$(CB)$ across $m_2$ to $DB'''$ leads to four congruent triangles:
\begin{eqnarray*}
\triangle_6' \cong \triangle_5' \cong \triangle_5 \cong \triangle_6 \\
\end{eqnarray*}
The first two are only in the bi-angle, the last two are only in
pentahouse.
\item [Step 8:] From now on it just repeats, except that there are longer
and longer chains of reflections between the corresponding triangles in
the bi-angle and the pentahouse.
\end{itemize}
We close in appealing to a second geometrical concept, \textit{continuity}.
Recall that Euclid tacitly assumed this for the case of overlapping circles
to actually intersect at points. Here we use it as follows:
By continuity we fill up the infinite region with pairs of triangles which
are congruent to their cousins in the finite pentagonal region.
Thus the infinite region inside the biangle must have the same finite area
as the pentahouse. And we have shown that biangles too have finite area.
\subsection{Monangles and Nulangles also have Finite Area}
Dissect the monangle into two adjacent biangles by a cevian from the
vertex of the single positive angle. (A cevian is a line connecting
the vertex of a triangle to the opposite side.) The area of the
monangle is, thus the sum of the finite areas of the two biangles.
And there are many more ways to dissect an ideal triangle (nulangle)
to complete this proof. But there is one in particular that will
interest us.
\section{Preview}
Next, we need to actually measure the area of triangles, beginning,
odlly enough, with nulangles, then monangles. Finally actual triangles.
\end{document}
Recall that in the Euclidean plane, a reflection across a mirror line
entails moving every point on one side of the mirror to a point on the
other along a perpendicular and the same distance. In other words,
the mirror is the perpendicular bisector between a point and its reflection
in the mirror.
If we use our familiar Poincare disk model, we can define such a reflection
as follows. Suppose The mirror is the line $(PQ)$, use an isometry $h_{PQ}$
which takes it to the real-line by sending $P \mapsto 0$ and
"endpoints" $P',Q'$ of $(PQ)$ to $-1, +1$ . We can use crossratios to
define it implicitly thus:
\[ CR(h_{PQ}(z), -1,0,1)=CR(z,P',P,Q')$ \]
Note that, being an isometry, it also sends $Q \mapsto d_H(P,Q)$.
Reflections across the real axis, $w\mapsto \bar{w}$
is clearly a reflection which is expressed by taking the conjugate.
So \[\sigma_{PQ}(z) = h_{PQ}^{-1}(\bar{h_{PQ}(z)})\]
is the general reflection across $(PQ)$.
However, in the Klein Model there is a more constructive way of doing this
and we shall have a look at it later. Here we only need to know that
\textbf{K-reflection lemma:} Given a mirror line $m$ crossed by line $k$ with
point $K$ on it, the reflection proceeds in 5 steps as shown in the figure so
labelled.
\subsection{Completion of the Proof of Biangle Theorem}
\begin{itemize}
\item [Step 4:] Draw mirror $m_1 = (AE)$ and reflect $B \mapsto B'$.
\item [Step 5:] Since $m_1 \perp (CD) $ we have that
\begin{eqnarray*}
\sigma_1(CD) & = & (DC) \\
\sigma_1(A) & = & (A) \\
\sigma_1(CB)& = &(DB') \\
\sigma_1(PB)& = &(PB') \\
\sigma_1(\triangle_1)& = & \triangle_2\\
\triangle_1 & \cong & \triangle_2\\
\triangle_3 & \cong & \triangle_4\\
\end{eqnarray*}
\item [Step 6:] Since $m_1 \perp (CD) $ we have that
Note that 3 of these triangles are in two regions: the original
biangle $\triangle ABC$ and the pentagonal \textit{pentahouse}
$ABFF'B'$. But $\triangle_4$ is only in the pentahouse.
\item [Step 6:] A second mirror $m_2=(PB')$, with reflection $\sigma_2$
lets us find a congruent cousin to $\triangle _{4'}$, which is only inside
the biangle.
\begin{eqnarray*}
\triangle_3&=&\sigma_1(\triangle_4) \\
\triangle_{4'}&=&\sigma_2(\triangle_3) \\
\end{eqnarray*}
\item [Step 7:]
The strategy is now apparent. We have reflected $(CB)$ across
$(DB')$ to obtain $(DB'')=m_2$, the next mirror.
\item [Step 8:] Reflecting
$(CB)$ across $m_2$ to $DB'''$ leads to four congruent triangles:
\begin{eqnarray*}
\triangle_6' \cong \triangle_5' \cong \triangle_5 \cong \triangle_6 \\
\end{eqnarray*}
The first two are only in the bi-angle, the last two are only in
pentahouse.
\item [Step 8:] From now on it just repeats, except that there are longer
and longer chains of reflections between the corresponding triangles in
the bi-angle and the pentahouse.
\end{itemize}
We close in appealing to a second geometrical concept, \textit{continuity}.
Recall that Euclid tacitly assumed this for the case of overlapping circles
to actually intersect at points. Here we use it as follows:
By continuity we fill up the infinite region with pairs of triangles which
are congruent to their cousins in the finite pentagonal region.
Thus the infinite region inside the biangle must have the same finite area
as the pentahouse. And we have shown that biangles too have finite area.
\subsection{Monangles and Nulangles also have Finite Area}
Dissect the monangle into two adjacent biangles by a cevian from the
vertex of the single positive angle. (A cevian is a line connecting
the vertex of a triangle to the opposite side.) The area of the
monangle is, thus the sum of the finite areas of the two biangles.
And there are many more ways to dissect an ideal triangle (nulangle)
to complete this proof. But there is one in particular that will
interest us.
\section{Preview}
Next, we need to actually measure the area of triangles, beginning,
odlly enough, with nulangles, then monangles. Finally actual triangles.
\end{document}
Non-EuclideanArea and Gauss' Theorem (Part 1)
\textit{(C) 2004, 2015 George K. Francis, Mathematics Department, University of Illinois} \begin{document} \maketitle \section{Introduction} Informally, everybody knows what area is. The area of a bounded plane region is a positive number. (A region is bounded if it fits inside a sufficiently large circle.) The area of two non-overlapping regions is the sum of the areas of each. As the very name of the subject says, the earliest task of geometry was to measure the area of real-estate for the ancient farming civilizations . We all agree that the area of a rectangle is the product of its base times its height. And some still rememember the area of a trapezoid from high school. As we have seen, there are no rectangles in non-Euclidean geometry to measure. However, as we shall see in this lesson, non-Euclidean the area of non-Euclidean triangles is proportional to their angle defect. Non-Euclidean ancients would have needed only a protractor to measure areas of agricultural plots instead of a complicated surveying science. But, as we have already seen, the price of this convenience is the absence of similarity and hence impossibility of scaling shapes to make the larger or smaller. In what follows we will refer to another plane geometry where the postulates of Euclidean geometry do not hold. The geometry of the surface of a sphere, or \textit{spherical geometry} were well known to Euclid. And imagining the differences between Euclidean areas and spherical areas is relatively easy and instructive. So we (again) adopt the synonym \textit{hyperbolic geometry} for non-Euclidean geometry properly, along with spherical geometry. \section{Areas by Dissection } From just a few rules, practically everything we need to know about areas can be deduced by elementary methods of \textit{dissection} (cutting and pasting), and when that fails, by the integral calculus. But to actually assign a number to an area, we need a unit of measurement, microns, inches, meters, light-years. Similar figures have proportional areas. The proportion is the square of the proportion of their linear measures: double the side of a square, and it's area quadruples.
 This figure reminds you how to deduce the area of a triangle
by dissection from the area of a rectangle. The Greeks, who
preferred beauty over practicality, also knew how to relate
the area $ab$ of a rectangle to that of a square of side $s$.
Recall their \textit{geometric mean}, $s = \sqrt{ab}$ was
constructible. Indeed, geometers like Newton still referred to finding
the area under a curve as \textit{squaring the figure}. (Finding the
length of a curve, which Newton also used his calculus for, was called
\textig{rectifying the curve} since, to the Greeks, it meant constructing
a segment of that length.
this lesson.
\section{On the Sphere }
On the sphere, triangles have an angle sum greater than $\pi$.
Experimenting with a dynamical geometry construction package, such as
such as GEX2.0, or with some spherical trigonometry leads you to discover
the \textin{angular excess theorem} for spherical geometry. One
example can be done in your head. Imagine walking west on the
equator and making a right turn, heading due north. At the north
pole make another right turn, heading south. At the equator you
will have made a rectangular triangle. Compared to a Euclidean
triangle, it has one too many right angles. It has angular excess of
$\pi/2$.
\section{On the Hyperbolic Plane}
Recall the construction that showed that the Euclidean
\textit{Exterior Angle Theorem} (EXAT) fails to be true in the
Klein model of $\mathbb{H}^2$. The amount by which it fails to be true
is also the angular defect, because the exterior angle opposite two
interior angles $\alpha, \beta$ is $c=\pi-\gamma$. Hence
\[c - (\alpha + \beta) = \pi -(\alpha+\beta+\gamma) = \mbox{defect} \]
This too may be determined experimentally with Hvidsten's GEX2.0
or Joel Castellano's \textit{NonEuclid}. The smaller the triangle,
the smaller the angular defect. And, as you moved the vertices
closer to the boundary unit circle of the Poincar'e disk, the defect
approached zero.
The method of dissection alone suffices to determine that angular defect,
like area, is \textit{additive}, in the sense that the angular defect of
of a triangle composed of the sum of two adjacent triangle is the sum of
their angular defects.
This figure reminds you how to deduce the area of a triangle
by dissection from the area of a rectangle. The Greeks, who
preferred beauty over practicality, also knew how to relate
the area $ab$ of a rectangle to that of a square of side $s$.
Recall their \textit{geometric mean}, $s = \sqrt{ab}$ was
constructible. Indeed, geometers like Newton still referred to finding
the area under a curve as \textit{squaring the figure}. (Finding the
length of a curve, which Newton also used his calculus for, was called
\textig{rectifying the curve} since, to the Greeks, it meant constructing
a segment of that length.
this lesson.
\section{On the Sphere }
On the sphere, triangles have an angle sum greater than $\pi$.
Experimenting with a dynamical geometry construction package, such as
such as GEX2.0, or with some spherical trigonometry leads you to discover
the \textin{angular excess theorem} for spherical geometry. One
example can be done in your head. Imagine walking west on the
equator and making a right turn, heading due north. At the north
pole make another right turn, heading south. At the equator you
will have made a rectangular triangle. Compared to a Euclidean
triangle, it has one too many right angles. It has angular excess of
$\pi/2$.
\section{On the Hyperbolic Plane}
Recall the construction that showed that the Euclidean
\textit{Exterior Angle Theorem} (EXAT) fails to be true in the
Klein model of $\mathbb{H}^2$. The amount by which it fails to be true
is also the angular defect, because the exterior angle opposite two
interior angles $\alpha, \beta$ is $c=\pi-\gamma$. Hence
\[c - (\alpha + \beta) = \pi -(\alpha+\beta+\gamma) = \mbox{defect} \]
This too may be determined experimentally with Hvidsten's GEX2.0
or Joel Castellano's \textit{NonEuclid}. The smaller the triangle,
the smaller the angular defect. And, as you moved the vertices
closer to the boundary unit circle of the Poincar'e disk, the defect
approached zero.
The method of dissection alone suffices to determine that angular defect,
like area, is \textit{additive}, in the sense that the angular defect of
of a triangle composed of the sum of two adjacent triangle is the sum of
their angular defects.
 \textbf{Theorem:} The angle defect is additive.
\textbf{Proof:} We rewrite the angle defect of the sum of two triangles
formed by a Cevian of a third triangle.
\begin{eqnarray*}
\mbox{Defect of both}&=&\pi - (\alpha + (\gamma + \delta) + \eta ) \\
&=& (\pi - \alpha -\beta - \gamma) + \beta - \delta - \eta \\
&=& \mbox{left} + (\pi - \epsilon) -\delta - \eta \\
&=& \mbox{left} + (\pi - (\epsilon + \delta + \eta ) \\
&=& \mbox{left defect } + \mbox{ right defect}
\end{eqnarray*}
\section{Ideal Triangles}
Every triangle is a trilateral in that is is formed by three non-concurrent
lines. But the converse is not true, even in the Euclidean plane.
There, a trilateral could consists of two parallel rays attached to a line segment. That would be a \textit{bi-angle} because
it has only two proper angles.
\textbf{Theorem:} The angle defect is additive.
\textbf{Proof:} We rewrite the angle defect of the sum of two triangles
formed by a Cevian of a third triangle.
\begin{eqnarray*}
\mbox{Defect of both}&=&\pi - (\alpha + (\gamma + \delta) + \eta ) \\
&=& (\pi - \alpha -\beta - \gamma) + \beta - \delta - \eta \\
&=& \mbox{left} + (\pi - \epsilon) -\delta - \eta \\
&=& \mbox{left} + (\pi - (\epsilon + \delta + \eta ) \\
&=& \mbox{left defect } + \mbox{ right defect}
\end{eqnarray*}
\section{Ideal Triangles}
Every triangle is a trilateral in that is is formed by three non-concurrent
lines. But the converse is not true, even in the Euclidean plane.
There, a trilateral could consists of two parallel rays attached to a line segment. That would be a \textit{bi-angle} because
it has only two proper angles.
 In $\mathbb{H}^2$ trilaterals come in four interesting kinds, look at the
Klein model. With three positive angles, it's an ordinary triangle.
With two angles, but with two lines \textit{asymptotically parallel}
(in the model the lines meet on the boundary), we'll call it a
\textit{biangle}. But now we can have \textit{monangles}, with but one
positive angle. The \textit{nulangles}, which have no positive angles, are
of special interest, and these are often called by their historical
name \textit{ideal triangles}. (Only the first and last terms are universal in
geometry, the others I made up.)
What is significant about two asymptotic lines is that they are parallel in
that they do not meet in a hyperbolic point, but they do not have a common
perpendicular. No parallel hyperbolic lines have two common perpendiculars,
for that would form a forbidden rectangle. How different matters are in
non-Euclidean geometry! Only triangles have finite area in the Euclidean plane. The region between two Euclidean parallels and a transversal has infinite area.
(In on the sphere there are no parallels at all, and everything, even the entire
spherical plane has finite area.)
Not so, and that is what we shall show first, in the hyperbolic plane. We shall
next prove the main lemma to Gauss's Theorem. The theorem states that all
ideal triangles (nulangles) are congruent and have finite area $\pi$.
This is appropriate because all three angles of a nulangle are zero, hence
the angular defect is $\pi$.
\section{Finite Area Lemma}
Here we show that all four kinds of hyperbolic triangles we defined above
have finite area. We begin with biangles where the construction and proof
is the easiest to understand. And then use the method of dissection to
dispose of the other three by using biangles to measure their area.
\textbf{Theorem: } Biangles Have Finite Areas.
In $\mathbb{H}^2$ trilaterals come in four interesting kinds, look at the
Klein model. With three positive angles, it's an ordinary triangle.
With two angles, but with two lines \textit{asymptotically parallel}
(in the model the lines meet on the boundary), we'll call it a
\textit{biangle}. But now we can have \textit{monangles}, with but one
positive angle. The \textit{nulangles}, which have no positive angles, are
of special interest, and these are often called by their historical
name \textit{ideal triangles}. (Only the first and last terms are universal in
geometry, the others I made up.)
What is significant about two asymptotic lines is that they are parallel in
that they do not meet in a hyperbolic point, but they do not have a common
perpendicular. No parallel hyperbolic lines have two common perpendiculars,
for that would form a forbidden rectangle. How different matters are in
non-Euclidean geometry! Only triangles have finite area in the Euclidean plane. The region between two Euclidean parallels and a transversal has infinite area.
(In on the sphere there are no parallels at all, and everything, even the entire
spherical plane has finite area.)
Not so, and that is what we shall show first, in the hyperbolic plane. We shall
next prove the main lemma to Gauss's Theorem. The theorem states that all
ideal triangles (nulangles) are congruent and have finite area $\pi$.
This is appropriate because all three angles of a nulangle are zero, hence
the angular defect is $\pi$.
\section{Finite Area Lemma}
Here we show that all four kinds of hyperbolic triangles we defined above
have finite area. We begin with biangles where the construction and proof
is the easiest to understand. And then use the method of dissection to
dispose of the other three by using biangles to measure their area.
\textbf{Theorem: } Biangles Have Finite Areas.
 For the proof of the
\begin{itemize}
\item [Step 1:]
In the figure the biangle $\triangle ABC$ is given. We extend the side
between its two positive angles $AB$ to a ray $AD$ where $D$ is on the
unit circle.
\item [Step 2:]
Note that $D$ is not a hyperbolic point, and $\triangle$ is, in fact,
a monangle with one side an entire hyperbolic line $\ell_{CD}$.
We shall need the pole of secant $CD$ to drop hyperbolic perpendiculars.
\item [Step 3:]
There are, at this point only two finite points, $A,B$, to connect to this
pole. And the perpendiculars to them cross the polar, $\ell_{CD}$, at
the points $E,F$ respectively.
\end{itemize}
\subsection{Hyperbolic Reflections}
At this point we pause the proof to explain that we need the hyperbolic
isometries (congruence) of reflections across a line in the Klein model.
We have not defined these yet. Here we shall merely make the plausible
and continue.
For the proof of the
\begin{itemize}
\item [Step 1:]
In the figure the biangle $\triangle ABC$ is given. We extend the side
between its two positive angles $AB$ to a ray $AD$ where $D$ is on the
unit circle.
\item [Step 2:]
Note that $D$ is not a hyperbolic point, and $\triangle$ is, in fact,
a monangle with one side an entire hyperbolic line $\ell_{CD}$.
We shall need the pole of secant $CD$ to drop hyperbolic perpendiculars.
\item [Step 3:]
There are, at this point only two finite points, $A,B$, to connect to this
pole. And the perpendiculars to them cross the polar, $\ell_{CD}$, at
the points $E,F$ respectively.
\end{itemize}
\subsection{Hyperbolic Reflections}
At this point we pause the proof to explain that we need the hyperbolic
isometries (congruence) of reflections across a line in the Klein model.
We have not defined these yet. Here we shall merely make the plausible
and continue.
 Recall that in the Euclidean plane, a reflection across a mirror line
entails moving every point on one side of the mirror to a point on the
other along a perpendicular and the same distance. In other words,
the mirror is the perpendicular bisector between a point and its reflection
in the mirror.
If we use our familiar Poincare disk model, we can define such a reflection
as follows. Suppose The mirror is the line $(PQ)$, use an isometry $h_{PQ}$
which takes it to the real-line by sending $P \mapsto 0$ and
"endpoints" $P',Q'$ of $(PQ)$ to $-1, +1$ . We can use crossratios to
define it implicitly thus:
\[ CR(h_{PQ}(z), -1,0,1)=CR(z,P',P,Q')$ \]
Note that, being an isometry, it also sends $Q \mapsto d_H(P,Q)$.
Reflections across the real axis, $w\mapsto \bar{w}$
is clearly a reflection which is expressed by taking the conjugate.
So \[\sigma_{PQ}(z) = h_{PQ}^{-1}(\bar{h_{PQ}(z)})\]
is the general reflection across $(PQ)$.
However, in the Klein Model there is a more constructive way of doing this
and we shall have a look at it later. Here we only need to know that
\textbf{K-reflection lemma:} Given a mirror line $m$ crossed by line $k$ with
point $K$ on it, the reflection proceeds in 5 steps as shown in the figure so
labelled.
\subsection{Completion of the Proof of Biangle Theorem}
\begin{itemize}
\item [Step 4:] Draw mirror $m_1 = (AE)$ and reflect $B \mapsto B'$.
\item [Step 5:] Since $m_1 \perp (CD) $ we have that
\begin{eqnarray*}
\sigma_1(CD) & = & (DC) \\
\sigma_1(A) & = & (A) \\
\sigma_1(CB)& = &(DB') \\
\sigma_1(PB)& = &(PB') \\
\sigma_1(\triangle_1)& = & \triangle_2\\
\triangle_1 & \cong & \triangle_2\\
\triangle_3 & \cong & \triangle_4\\
\end{eqnarray*}
\item [Step 6:] Since $m_1 \perp (CD) $ we have that
Note that 3 of these triangles are in two regions: the original
biangle $\triangle ABC$ and the pentagonal \textit{pentahouse}
$ABFF'B'$. But $\triangle_4$ is only in the pentahouse.
\item [Step 6:] A second mirror $m_2=(PB')$, with reflection $\sigma_2$
lets us find a congruent cousin to $\triangle _{4'}$, which is only inside
the biangle.
\begin{eqnarray*}
\triangle_3&=&\sigma_1(\triangle_4) \\
\triangle_{4'}&=&\sigma_2(\triangle_3) \\
\end{eqnarray*}
\item [Step 7:]
The strategy is now apparent. We have reflected $(CB)$ across
$(DB')$ to obtain $(DB'')=m_2$, the next mirror.
\item [Step 8:] Reflecting
$(CB)$ across $m_2$ to $DB'''$ leads to four congruent triangles:
\begin{eqnarray*}
\triangle_6' \cong \triangle_5' \cong \triangle_5 \cong \triangle_6 \\
\end{eqnarray*}
The first two are only in the bi-angle, the last two are only in
pentahouse.
\item [Step 8:] From now on it just repeats, except that there are longer
and longer chains of reflections between the corresponding triangles in
the bi-angle and the pentahouse.
\end{itemize}
We close in appealing to a second geometrical concept, \textit{continuity}.
Recall that Euclid tacitly assumed this for the case of overlapping circles
to actually intersect at points. Here we use it as follows:
By continuity we fill up the infinite region with pairs of triangles which
are congruent to their cousins in the finite pentagonal region.
Thus the infinite region inside the biangle must have the same finite area
as the pentahouse. And we have shown that biangles too have finite area.
\subsection{Monangles and Nulangles also have Finite Area}
Dissect the monangle into two adjacent biangles by a cevian from the
vertex of the single positive angle. (A cevian is a line connecting
the vertex of a triangle to the opposite side.) The area of the
monangle is, thus the sum of the finite areas of the two biangles.
And there are many more ways to dissect an ideal triangle (nulangle)
to complete this proof. But there is one in particular that will
interest us.
\section{Preview}
Next, we need to actually measure the area of triangles, beginning,
odlly enough, with nulangles, then monangles. Finally actual triangles.
\end{document}
Recall that in the Euclidean plane, a reflection across a mirror line
entails moving every point on one side of the mirror to a point on the
other along a perpendicular and the same distance. In other words,
the mirror is the perpendicular bisector between a point and its reflection
in the mirror.
If we use our familiar Poincare disk model, we can define such a reflection
as follows. Suppose The mirror is the line $(PQ)$, use an isometry $h_{PQ}$
which takes it to the real-line by sending $P \mapsto 0$ and
"endpoints" $P',Q'$ of $(PQ)$ to $-1, +1$ . We can use crossratios to
define it implicitly thus:
\[ CR(h_{PQ}(z), -1,0,1)=CR(z,P',P,Q')$ \]
Note that, being an isometry, it also sends $Q \mapsto d_H(P,Q)$.
Reflections across the real axis, $w\mapsto \bar{w}$
is clearly a reflection which is expressed by taking the conjugate.
So \[\sigma_{PQ}(z) = h_{PQ}^{-1}(\bar{h_{PQ}(z)})\]
is the general reflection across $(PQ)$.
However, in the Klein Model there is a more constructive way of doing this
and we shall have a look at it later. Here we only need to know that
\textbf{K-reflection lemma:} Given a mirror line $m$ crossed by line $k$ with
point $K$ on it, the reflection proceeds in 5 steps as shown in the figure so
labelled.
\subsection{Completion of the Proof of Biangle Theorem}
\begin{itemize}
\item [Step 4:] Draw mirror $m_1 = (AE)$ and reflect $B \mapsto B'$.
\item [Step 5:] Since $m_1 \perp (CD) $ we have that
\begin{eqnarray*}
\sigma_1(CD) & = & (DC) \\
\sigma_1(A) & = & (A) \\
\sigma_1(CB)& = &(DB') \\
\sigma_1(PB)& = &(PB') \\
\sigma_1(\triangle_1)& = & \triangle_2\\
\triangle_1 & \cong & \triangle_2\\
\triangle_3 & \cong & \triangle_4\\
\end{eqnarray*}
\item [Step 6:] Since $m_1 \perp (CD) $ we have that
Note that 3 of these triangles are in two regions: the original
biangle $\triangle ABC$ and the pentagonal \textit{pentahouse}
$ABFF'B'$. But $\triangle_4$ is only in the pentahouse.
\item [Step 6:] A second mirror $m_2=(PB')$, with reflection $\sigma_2$
lets us find a congruent cousin to $\triangle _{4'}$, which is only inside
the biangle.
\begin{eqnarray*}
\triangle_3&=&\sigma_1(\triangle_4) \\
\triangle_{4'}&=&\sigma_2(\triangle_3) \\
\end{eqnarray*}
\item [Step 7:]
The strategy is now apparent. We have reflected $(CB)$ across
$(DB')$ to obtain $(DB'')=m_2$, the next mirror.
\item [Step 8:] Reflecting
$(CB)$ across $m_2$ to $DB'''$ leads to four congruent triangles:
\begin{eqnarray*}
\triangle_6' \cong \triangle_5' \cong \triangle_5 \cong \triangle_6 \\
\end{eqnarray*}
The first two are only in the bi-angle, the last two are only in
pentahouse.
\item [Step 8:] From now on it just repeats, except that there are longer
and longer chains of reflections between the corresponding triangles in
the bi-angle and the pentahouse.
\end{itemize}
We close in appealing to a second geometrical concept, \textit{continuity}.
Recall that Euclid tacitly assumed this for the case of overlapping circles
to actually intersect at points. Here we use it as follows:
By continuity we fill up the infinite region with pairs of triangles which
are congruent to their cousins in the finite pentagonal region.
Thus the infinite region inside the biangle must have the same finite area
as the pentahouse. And we have shown that biangles too have finite area.
\subsection{Monangles and Nulangles also have Finite Area}
Dissect the monangle into two adjacent biangles by a cevian from the
vertex of the single positive angle. (A cevian is a line connecting
the vertex of a triangle to the opposite side.) The area of the
monangle is, thus the sum of the finite areas of the two biangles.
And there are many more ways to dissect an ideal triangle (nulangle)
to complete this proof. But there is one in particular that will
interest us.
\section{Preview}
Next, we need to actually measure the area of triangles, beginning,
odlly enough, with nulangles, then monangles. Finally actual triangles.
\end{document}