Exercises in Klein Model Constructions
\begin{document}
last edited 26apr15
\maketitle
These problems involve constructions and annotated figures, which can be
realized by GGB or GEX, and also by hand using a compass and transparent
plastic 30-60-90 triangle.
\begin{itemize}
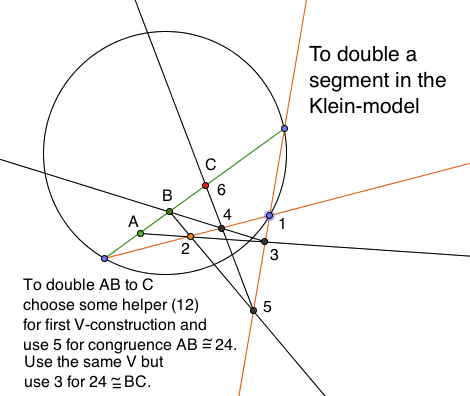
\item[Problem 0:] The solution to the lab exercise on F13 may be deduced
from the
Doubling figure .
\item[Problem 1:] Recall how we defined perpendiculars in the Klein model using
the polar of a secant in the unit circle. Given two k-parallel lines that
do not meet, even on the unit circle, demonstrate how to construct the single
common k-perpendicular. (This again shows that non-Euclidean parallel lines have
at most one common perpendicular. Recall how we originall proved this
using Lambert quadrilaterals.)
\item[Problem 2:] Demonstrate experimentally, by submitting a .ggb or a
.gex construction, that being perpendicular to each other is a reflexive
relation for lines. In other words, show that, given a line $m$, that if
line $k$ is
constructed perpendicular to $m$, then $m$ must also be the line perpendicular
to $k$ at $(km)$. (Comment: This is difficult to prove rigorously in
classical Euclidean geometry without the developing the theory of circular
secants.)
\item[Problem 3:]
Demonstrate experimentally, by submitting a .ggb or a
.gex construction, that two perpendiculars to a line are in perspective
from a point on the Euclidean extension of the given line. Hint:
you can continue your construction from Problem 2 to solve this problem.
(Comment: this is even more difficult to prove synthetically.
\item[Problem 4:] Recall the
N-construction
we did in class. Generalize the N-construction
to the case of two intersecting line $(AB)$ and $(CD)$. (Careful, $A,B,C$ are
k-points inside the Klein disk, and $D$ is an ideal point on the unit circle.
This the \textit{X-construction}, and it also
also uses two V-constructions to move the given segment $AB$ first to a
helper line, and then to the given ray.
Hint: The intermediate helper line still connects
$D$ to $5$. Unless $C$ is where the two lines cross, $(AC)$ still becomes the
common base line for both V-constructions.
\item[Problem 5:] Solve the previous problem for the special case that
$A=C=(AB)(CD)$. Note that his is the case where we want to use the segment
$AB$ as the radius of a k-circle centered at $A$, as we discussed in lab.
\item[Problem 6:]
This special X-construction in Problem 5 is simpler for doubling a segment.
Use for helper line one that crosses at the endpoint in which direction you
plan to double the segment.
\item[Problem 7:]
Demonstrate how to use the X-doubling construction in
Problem 6 to that show that the point found in the
Halving Construction really is the
midpoint of the segment. Hint: Use just one of the helper lines to
make an X with the given line the segment resides on.
\end{itemize}
\end{document}
 \begin{itemize}
\item[Problem 0:] The solution to the lab exercise on F13 may be deduced
from the Doubling figure .
\item[Problem 1:] Recall how we defined perpendiculars in the Klein model using
the polar of a secant in the unit circle. Given two k-parallel lines that
do not meet, even on the unit circle, demonstrate how to construct the single
common k-perpendicular. (This again shows that non-Euclidean parallel lines have
at most one common perpendicular. Recall how we originall proved this
using Lambert quadrilaterals.)
\item[Problem 2:] Demonstrate experimentally, by submitting a .ggb or a
.gex construction, that being perpendicular to each other is a reflexive
relation for lines. In other words, show that, given a line $m$, that if
line $k$ is
constructed perpendicular to $m$, then $m$ must also be the line perpendicular
to $k$ at $(km)$. (Comment: This is difficult to prove rigorously in
classical Euclidean geometry without the developing the theory of circular
secants.)
\item[Problem 3:]
Demonstrate experimentally, by submitting a .ggb or a
.gex construction, that two perpendiculars to a line are in perspective
from a point on the Euclidean extension of the given line. Hint:
you can continue your construction from Problem 2 to solve this problem.
(Comment: this is even more difficult to prove synthetically.
\item[Problem 4:] Recall the N-construction
we did in class. Generalize the N-construction
to the case of two intersecting line $(AB)$ and $(CD)$. (Careful, $A,B,C$ are
k-points inside the Klein disk, and $D$ is an ideal point on the unit circle.
This the \textit{X-construction}, and it also
also uses two V-constructions to move the given segment $AB$ first to a
helper line, and then to the given ray.
Hint: The intermediate helper line still connects
$D$ to $5$. Unless $C$ is where the two lines cross, $(AC)$ still becomes the
common base line for both V-constructions.
\item[Problem 5:] Solve the previous problem for the special case that
$A=C=(AB)(CD)$. Note that his is the case where we want to use the segment
$AB$ as the radius of a k-circle centered at $A$, as we discussed in lab.
\item[Problem 6:]
This special X-construction in Problem 5 is simpler for doubling a segment.
Use for helper line one that crosses at the endpoint in which direction you
plan to double the segment.
\item[Problem 7:]
Demonstrate how to use the X-doubling construction in
Problem 6 to that show that the point found in the
Halving Construction really is the
midpoint of the segment. Hint: Use just one of the helper lines to
make an X with the given line the segment resides on.
\end{itemize}
\end{document}
\begin{itemize}
\item[Problem 0:] The solution to the lab exercise on F13 may be deduced
from the Doubling figure .
\item[Problem 1:] Recall how we defined perpendiculars in the Klein model using
the polar of a secant in the unit circle. Given two k-parallel lines that
do not meet, even on the unit circle, demonstrate how to construct the single
common k-perpendicular. (This again shows that non-Euclidean parallel lines have
at most one common perpendicular. Recall how we originall proved this
using Lambert quadrilaterals.)
\item[Problem 2:] Demonstrate experimentally, by submitting a .ggb or a
.gex construction, that being perpendicular to each other is a reflexive
relation for lines. In other words, show that, given a line $m$, that if
line $k$ is
constructed perpendicular to $m$, then $m$ must also be the line perpendicular
to $k$ at $(km)$. (Comment: This is difficult to prove rigorously in
classical Euclidean geometry without the developing the theory of circular
secants.)
\item[Problem 3:]
Demonstrate experimentally, by submitting a .ggb or a
.gex construction, that two perpendiculars to a line are in perspective
from a point on the Euclidean extension of the given line. Hint:
you can continue your construction from Problem 2 to solve this problem.
(Comment: this is even more difficult to prove synthetically.
\item[Problem 4:] Recall the N-construction
we did in class. Generalize the N-construction
to the case of two intersecting line $(AB)$ and $(CD)$. (Careful, $A,B,C$ are
k-points inside the Klein disk, and $D$ is an ideal point on the unit circle.
This the \textit{X-construction}, and it also
also uses two V-constructions to move the given segment $AB$ first to a
helper line, and then to the given ray.
Hint: The intermediate helper line still connects
$D$ to $5$. Unless $C$ is where the two lines cross, $(AC)$ still becomes the
common base line for both V-constructions.
\item[Problem 5:] Solve the previous problem for the special case that
$A=C=(AB)(CD)$. Note that his is the case where we want to use the segment
$AB$ as the radius of a k-circle centered at $A$, as we discussed in lab.
\item[Problem 6:]
This special X-construction in Problem 5 is simpler for doubling a segment.
Use for helper line one that crosses at the endpoint in which direction you
plan to double the segment.
\item[Problem 7:]
Demonstrate how to use the X-doubling construction in
Problem 6 to that show that the point found in the
Halving Construction really is the
midpoint of the segment. Hint: Use just one of the helper lines to
make an X with the given line the segment resides on.
\end{itemize}
\end{document}