Fourteenth Week of the Course
Bolzano's Intermediate Value Theorem
last updated 1jul13 formerly 26apr11, 23apr12\begin{document} \maketitle \section{Introduction} In 1817 Bernhard Bolzano published a very modern proof of the \textit{ Intermediate Value Theorem} (IVT) for continuous functions. Unfortunately, he was obliged to publish in an obscure Bohemian journal. Cauchy's 1821 proof was better received. In contrast to Bolzano, Cauchy still used infinitesimals, a concept that found logical vindication only in the past century. Weierstrass' proof in 1854 is the best known. Bolzano needed a lemma, that every bounded, infinite sequence of reals has a convergent subsequence. This, today, is known as the \textit{Bolzano-Weierstrass Theorem} (BWT). The IVT says that if $f$ is continuous on $[a,b]$ and $f(a) \lt u \lt f(b)$ then there exists some $ a \lt c \lt b$ for which $u=f(c)$. Contemporary proofs are usually based on the \textit{Least Upper Bound Principle}(LUBP), that a nonempty, bounded-above set of real numbers has a lub. In a previous lesson we saw the relation between the LUBP and \textit{ Bolzano's Lemma}(BWT) as equivalent axiomatic properties of the real numbers. We next discuss a screen capture of the proof in Wikipedia for Bolzano's IVT.
\section{Proof of the Intermediate Value Theorem}
Above, we quote a proof by Wikipedia. The proof is correct, but it leaves
several steps to the readeer, which a beginner would easily miss. Either
the beginner draws a picture, whence everything stated is "obvious", or
is unable to fill in the gaps.
Firstly, the Wikipedist uses the "below set", $S = \{x\in [a,b] | f(x) \lt u \} $.
Since we assumed that $f(a) < u $ we know that $a \in S$. And since
we assumed that $f(b) > u $ we know that $b \in ub(S)$. Stop and think,
there something profound going on here.
Clearly every $x$ in the interval $[a,b]$ has the property
that $x \lt b$. Since the Wikipedia proof assumes that $S \in [a,b]$ ,
doesn't that make $b$ an upper bound of $S$ as well?
Since it is an upper bound whether or not we assume $f(b) > u$, we shall
have to use this hypothesis somewhere else in the proof, but not here. Remember,
one way to check your proof is to check that every hypothesis is actually
used. Note that all the hypothesis says is that $b \notin S$.
Next, knowing from the LUBP that $c:= lub(S)$ exists, we expect to be able
to deduce our immediate conjecture that $f(c)=u$ just from the following ingredients:
\begin{itemize}
\item $f$ is continuous at $x=c$
\item $c$ is \textbf{an} upper bound for $S$
\item $c$ is \textbf{the least} of all upper bounds of $S$
\item and, let's not forget that $ b\notin S$
\end{itemize}
Since we want to conclude that $f(c)=u$ we'll build a contradiction from
assuming it does not.
\subsection{The case that $u \lt f(c)$ }
We chose the positive number $f(c) - u$ as our continuity epsilon, and
obtain a $\delta \gt 0$ so that
\[(\forall x \in (c-\delta, c+\delta) )( |f(x)-f(c)| \lt f(c) - u ) .\]
Undoing the absolute value we use the left-inequality
\[ -(f(c)-u) \lt f(x) - f(c) \Rightarrow u \lt f(x) .\]
Recall that we assumed that $c$ was an upper bound for $S$. That means
there are no $f(x) < u$ once $c \le x $. But now we have to admit
that there
aren't any of them in $(c-\delta, c)$ either. So $c-\delta$ is
a better upper bound that $c$. This contradicts that $c$ is the \textbf{least}
upper bound. So, we can reject half of the assumption that $f(c)\ne u$.
\subsection{The case the $ f(c) \lt u $}
This time we take the positive number $u-f(c)$ as our continuity epsilon at $c$.
We again find a $\delta$ interval about $c$ so that
\[ (\forall x \in (c-\delta, c+\delta))(|f(x)-f(c)| \lt u - f(c) ) .\]
This time we expect to use the right inequality of the undone absolute
values
\[ f(x) -f(c) \lt u - f(c) \Rightarrow f(x) \lt u \mbox{ i.e. } x \in S .\]
So, we conclude that $(\forall x \in (c, c + \delta))(x \in S).$ Even
one element of $S$ to the right of $c$ would put the lie to $c$ being an
upper bound. Now we have an entire interval of them, and an uncountably
many contradictions. One suffices, and we can reject the other half of
the assumption that $f(c)\ne u$.
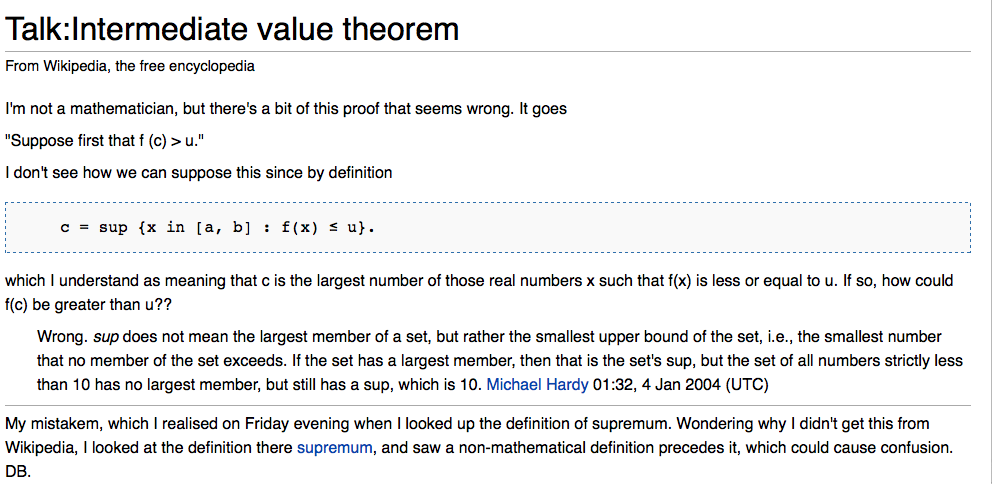The Wikipedia article where this proof was presented had an objection
which the authors kindly left around for contemplation. As you see, the
use of the word "supremum" for "lub" easily leads to misunderstandings.
To give you some assurance that you understand this proof, here is a
useful variant of the problem. You should solve it in this form when you
enter the IVT into your Journal. Note that we actually found that
$limsup(\{ x | f(x) \lt u \})$ is the last value of $x$ to the right
for which $f(x)=u$. Suppose you chose $ glb(\{x \in [a,b] | f(x) > u \}$
for your solution. How would the argument go in this case? To appreciate
this approach, consider the example of $f(x)=sin(x)$ on the interval
$a=-\pi/4, b=+13\pi/4$ and chose $c=0$. Which zero of the sine function
does each of the above approaches actually find?
\section{Maxima and Minima Achieved}
Another essential property of continuous function on closed intervals, is
their achievement of a minimal and a maximal value on the interval. That is,
\[f \mbox{ continuous on } [a,b] \Rightarrow
(\exists a \le m \le b)( f(m) = max f([a,b]) .\]
Recall that for a set $S$, $f(S) = \{f(x) | x\in S \}$. To prove this we
first have to agree that the RHS is even a number, namely that the set
$Y := f([a,b])$ has a maximum. It might not even be bounded above, until
we prove that it is. Even then, it might just have a lub and not a maximum.
And even if it has a maximum, it might not be the value of $f$ anywhere
on the interval.
We review what it means for a set $Y$ to be bounded above, by considering
what it means for a set not to be bounded above.