The Second Lesson of the Course
Commentary on Chapter 2 of D'Angelo-West Text
24jan11, 21may13, 23may13\begin{document} \maketitle
Summary
In this lesson you will review set theory, and learn the symbolic vocubulary for mathematical statements and proofs. \section{Introduction} Chapter 2 of our textbook is chiefly concerned with mathematical language. More precisely, it lightly treats the notation and application of three areas of logic, \begin{enumerate} \item Set Theory, as in $ A \subset (A \union B) $ and $ A = \{x| x\in A \}$. \\ \item Propositional Logic, as in $ (P \implies Q) \equiv (\neg P \or Q)$. \\ \item Predicate Calculus, as in $ (\forall \epsilon > 0)(\exists \delta > 0) (\forall 0 < x <\delta) (|\frac{\sin(x)}{x} - 1| < \epsilon )$. \\ \end{enumerate}
Quetion1: Prove that$ A \subset (A \union B)$ and $(A \cap B) \subset A$.
Hint: Show that if $x \in LHS$ then $x \in RHS$.
Here is a translation of these symbolic statements in common speech.
\begin{enumerate}
\item The set $A$ is a subset of the union of sets $A$ and $B$.
\item The proposition "$P$ implies $Q$" is equivalent to the
proposition "either the negation of $P$ or $Q$ is true".
\item For all positive numbers $\epsilon$ there exists a positive
$\delta$ such that for all positive $x$ smaller than $\delta$ the
ratio of $\sin(x)$ to $x$ is smaller than $\epsilon$.
\end{enumerate}
Note how common speech is inadequate to express the mathematical statements
without ambiguity. For example, in (2) does "or" mean that
$\neg P$ or $Q$ must be false? Again, in (3), is the $\delta$ the
same for all $\epsilon$? Neither of these is correct.
Question 2 : Use the concept of limit to give another paraphrase of (3).
We'll assume you're familiar with Set Theory and are willing to accept
a slightly more rigorous introduction to \textit{propositional logic}
than Chapter 2 of D'Angelo-West provides. However, you can learn to
use \textit{ quantified propositions} correctly from observation and
practice. A rigororous introduction to this is the subject of a first
course is logic.
\section{Propositional Logic}
To test the validity of compound statements we use the concept of
truth tables. For typographical reasons we refer you to the
LaTeX document on
Truth Tables next. Many LaTeX structures in this
document would be too difficult to reproduce here. Since you will want
to use similar notation, you will find both \texttt{ truth.tex} and
\texttt{truth.pdf} in Advice > LaTeX Sampler. You can download both files.
On a PC you will have to rename \texttt{truth.tex} to \texttt{turth.txt}
before Wordpad will open the file. Note that the only difference between
these two files is the suffix in their names. In most browsers, you
can read \texttt{truth.pdf} by just selecting it (clicking on it).
By the middle of the term you will be able to read (most of) the LaTeX
code in \texttt{truth.tex}. LaTeX is a language you learn by using it.
To see what a LaTeX phrase means, and to experiment modifying it, you
can use texPad. But note, if you do use texPad, you may have to use
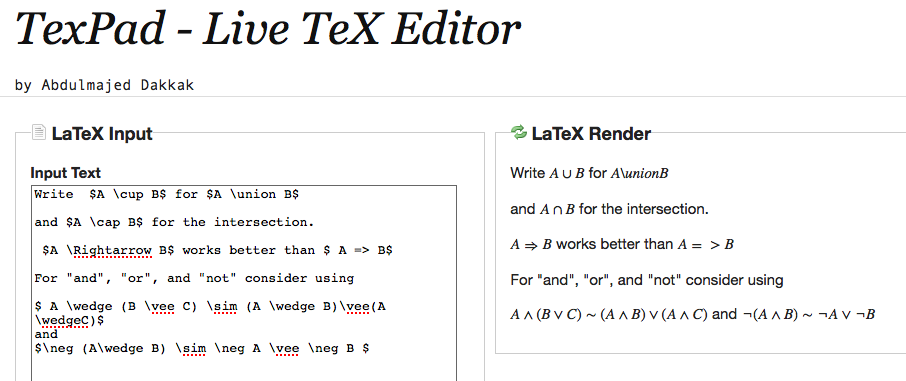 less mathematical sounding names for the same symbol, for example
"cup" for "union", "Rightarrow" for "implies" etc.
Here is an example created with texPad. The MathML compliant LaTeX
code is on the left, and the symbolic output is on the right.
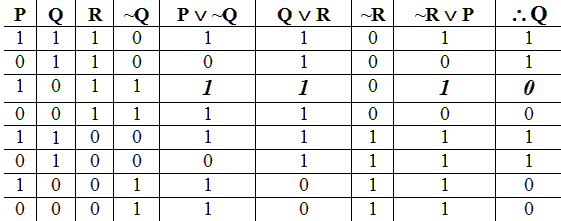
The truthtable in the first illustration at the begining of this
lesson matches most closely the exposition in D'Angelo-West,
except that they use the more anglo-centric letters T and F
for "true" and "false" than our 1 and 0.
Finally, plaintext (e.g. email math) you can improvise some logical symbols.
For "and" you can use the carat ^ symbol, for "or" use a lower case v,
for "implies" use =>. Use the tilde ~ for equivalence $\equiv$. But note
in the illustration that its basic LaTeX name is "sim" for "similar."
Since two compound propositions are equivalent if and only if their
truth values are the same (for given truth values of the component of
the compound), it is not incorrect to use the = sign in plaintext for equivalence.
Thus "(B v notB) = 1" says that whether "B=1" or "B=0", Hamlet's tautology,
"B v notB" is true regardless. Finally, you can always use the LaTe codes
and your mathematal correspondent will understand what you mean.
\section{Filecard Questions}
After you have studied the lesson on truthtables linked to this page, please
answer the following.
less mathematical sounding names for the same symbol, for example
"cup" for "union", "Rightarrow" for "implies" etc.
Here is an example created with texPad. The MathML compliant LaTeX
code is on the left, and the symbolic output is on the right.
The truthtable in the first illustration at the begining of this
lesson matches most closely the exposition in D'Angelo-West,
except that they use the more anglo-centric letters T and F
for "true" and "false" than our 1 and 0.
Finally, plaintext (e.g. email math) you can improvise some logical symbols.
For "and" you can use the carat ^ symbol, for "or" use a lower case v,
for "implies" use =>. Use the tilde ~ for equivalence $\equiv$. But note
in the illustration that its basic LaTeX name is "sim" for "similar."
Since two compound propositions are equivalent if and only if their
truth values are the same (for given truth values of the component of
the compound), it is not incorrect to use the = sign in plaintext for equivalence.
Thus "(B v notB) = 1" says that whether "B=1" or "B=0", Hamlet's tautology,
"B v notB" is true regardless. Finally, you can always use the LaTe codes
and your mathematal correspondent will understand what you mean.
\section{Filecard Questions}
After you have studied the lesson on truthtables linked to this page, please
answer the following.
Question 3: Prove DeMorgan's Law
$ A \wedge (B \vee C)) \sim (A \wedge B)\vee (A \wedge C)$ by considering
truth values.
Question 4: What is $ A \vee (B \wedge C))$ equivalent to?
Question 5: Simplify $ \neg( A \Rightarrow B)$.
Question 6:
Why is the negation of $A \Rightarrow B$ not just $B \implies A$ ?
Question 7: Write "$A$ if and only if $B$" in symbols. Find its truth table.
\end{document}