Third Lesson of the Course
Commentary on Chapter 3 of D'Angelo-West Text
30jan11, revised in part 3feb16
\begin{document}
\maketitle
 Caution:
This commentary on D'Angelo-West was written
for online Netmath students who (1) had to purchase the textbook,
and (2), were far less mathematically prepared than the the current students
at Illinois. Therefore, it took a very low-level approach, but required
careful reading of the text. So, there is a different emphasis here,
which will be developed in the lectures. I will write this in blue.
Caution:
This commentary on D'Angelo-West was written
for online Netmath students who (1) had to purchase the textbook,
and (2), were far less mathematically prepared than the the current students
at Illinois. Therefore, it took a very low-level approach, but required
careful reading of the text. So, there is a different emphasis here,
which will be developed in the lectures. I will write this in blue.
\section{Introduction}
Chapter 3 of our textbook is concerned with the \textit{ Induction Axiom
of Arithmetic}. It is not an opinion, nor an experimental result that it
holds. It is an assumption which every mathematician accepts. Some logicians
test its validity by proposing alternatives, or rejecting it. But this is
not a logic course. Our purpose here is to understand how to apply this
axiom to prove theorems.
To understand this commentary without studying the textbook is not
advisable. However, you can read the commenatry first, and then the
textbook to see what I consider important.
To reduce clutter we shall usually forget to mention that we are talking only about
numbers in $\mathbb{N}$. In other words, in this context "number" shall mean a member of $\mathbb{N}$.
\section{Examples}
\subsection{The sum of odd numbers is square}
As stated, this is trivially false, for $3+5=8 \ne n^2 $ for any $n$.
So we must mean something else. From the picture it is obvious what
the theorem says and, perhaps you think it is also obviously true.
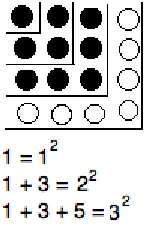 Question 1. State the theorem correctly in your own words.
In that case, you won't mind seeing a rigorous proof.
\begin{itemize}
\item For $ n=1$, it is the sum of the first odd number and is a square.
\item And $ n^2 + (2(n+1) -1) = n^2 + (2n +1 ) = (n+1)^2
\item Done!
\end{itemize}
Done what? \textbf{This is NOT a proof!} It is a fragment of a proof.
Indeed, it is the heart of a proof, but, as it stands, it doesn't
even make sense.
Question 2. List the chief faults of this "proof".
Here is a formal proof:
\begin{eqnarray*}
\mbox{Let } P(n)& = & (\sum_{k=1}^n (2k-1) = n^2) \\
P(1) & = & (\sum_{k=1}^1 (2k-1) = 2-1 = 1 = 1^2) \mbox{ half done} \\
P(n) & = & (\sum_{k=1}^n (2k-1) = n^2) \mbox{ hypothesis, so use it}\\
\mbox{ Calculate } \sum_{k=1}^{n+1} (2k-1) & = & \sum_{k=1}^{n} (2k-1) + (2n+1) \\
&=& P(n) + (2n+1) = n^2 + 2n+1 + 1 = (n+1)^2\\
\therefore & & P(n+1) \\
\end{eqnarray*}
Question 3. Where is the hypothesis used?
Now were done, because $P(1)$ holds and $P(n) \implies P(n+1)$ is true.
\subsection{Sermon}
So what's so difficult here? Some advice on induction problems:
\begin{enumerate}
\item Recognize the problem as being one amenable to finite induction.
\item Analyze the problem and formulate a conjecture (=tentative theorem)..
\item Test your conjectur for $n=1,2,3,4$.
\item Develop a strategy of proof, and compose one.
\item Check your work. What did you leave out?
\end{enumerate}
Here fit 100 practice problems. Put a couple simple ones into your Journal.
As you will notice when looking through the problems given in the D'Angelo-West,
they are either uninteresting, like the one above, or very obscure and difficult. For our purposes, you need to know how use the principle of induction, and to
uynderstand the difference between simple induction and so-called \textit{strong induction}
Question 1. State the theorem correctly in your own words.
In that case, you won't mind seeing a rigorous proof.
\begin{itemize}
\item For $ n=1$, it is the sum of the first odd number and is a square.
\item And $ n^2 + (2(n+1) -1) = n^2 + (2n +1 ) = (n+1)^2
\item Done!
\end{itemize}
Done what? \textbf{This is NOT a proof!} It is a fragment of a proof.
Indeed, it is the heart of a proof, but, as it stands, it doesn't
even make sense.
Question 2. List the chief faults of this "proof".
Here is a formal proof:
\begin{eqnarray*}
\mbox{Let } P(n)& = & (\sum_{k=1}^n (2k-1) = n^2) \\
P(1) & = & (\sum_{k=1}^1 (2k-1) = 2-1 = 1 = 1^2) \mbox{ half done} \\
P(n) & = & (\sum_{k=1}^n (2k-1) = n^2) \mbox{ hypothesis, so use it}\\
\mbox{ Calculate } \sum_{k=1}^{n+1} (2k-1) & = & \sum_{k=1}^{n} (2k-1) + (2n+1) \\
&=& P(n) + (2n+1) = n^2 + 2n+1 + 1 = (n+1)^2\\
\therefore & & P(n+1) \\
\end{eqnarray*}
Question 3. Where is the hypothesis used?
Now were done, because $P(1)$ holds and $P(n) \implies P(n+1)$ is true.
\subsection{Sermon}
So what's so difficult here? Some advice on induction problems:
\begin{enumerate}
\item Recognize the problem as being one amenable to finite induction.
\item Analyze the problem and formulate a conjecture (=tentative theorem)..
\item Test your conjectur for $n=1,2,3,4$.
\item Develop a strategy of proof, and compose one.
\item Check your work. What did you leave out?
\end{enumerate}
Here fit 100 practice problems. Put a couple simple ones into your Journal.
As you will notice when looking through the problems given in the D'Angelo-West,
they are either uninteresting, like the one above, or very obscure and difficult. For our purposes, you need to know how use the principle of induction, and to
uynderstand the difference between simple induction and so-called \textit{strong induction}
Here is an \textbf{Interesting Example 2}:
Consider the number of ways of enumerating (lining up in an order from first to last) a finite set. For example, of 5 people. There are 5 to chose as first,
4 for second, etc . So the answer is $n! = n(n-1)...1 $. The number of ways
to select a subset of items is $2^n$. Which is the larger ?
\begin{eqnarray*}
n! & \sim & 2^n \\
n=1 \implies 1& = & 1 \\
n=2 \implies 2 & < & 4 \\
n=3 \implies 6 & < & 8 \\
n=4 \implies 24 & > & 16 \\
n=5 \implies 120 & > & 32 \\
\end{eqnarray*}
\textbf{Conjecture:} $ (\forall n \ge 4)(n! > 2^n)$.
Let $ P(n)= (n! > 2^n)$.
\textbf{proof by induction}.
$P(1)$ was calculated above.
Consider that $P(n+1) = (n+1)!=(n+1)n! > (n+1)2^n > 2\; 2^n=2^{n+1}. QED
Here is an \textbf{Interesting Example 3} of an incorrect argument:
\textbf{Conjecture:} All people are right handed
The \textit{chirality} of a person is their \textit{handedness}; either
right or left.
We "prove" the theorem by first proving this
\textbf{Lemma:} All finite sets of people have the same chirality.
\textbf{proof by induction}.
$P(1)$ is obvious.
Now assume $P(n)$ and consider $P(n+1)$. Line them up in a row, and
note that the first $n$ people have, by the induction hypothesis, the
same chirality. Similarly, the last $n$ people. But clearly these two
sets overlap, they have some people in common. Hence all $n+1$ of them
have the same chirality.
Since I am right handed, all people are right handed! Where is the error?
\subsection{All primes are odd.}
Recall that a number divible only by itself and 1 is called a \textit{ prime number}.
Aha, you say. 2 is a prime and it is even. So the theorem is false. But
every other number after 2 is also even and therefore not prime. So maybe
if we ammend the statement we do get a theorem.
Question 4. State the correct theorem about odd primes.
So, do we really need finite induction here? No, but it is instructive to do
so anyway. So what should $P(n)$ read like? Maybe the $n$ counts the primes.
So we proceed thus
\begin{eqnarray*}
\mbox{Label the primes } & & p_1=2, p_2=3, p_3=5, \mbox{ etc } \\
\mbox{Define } P(n) & := & ( n \ge 2 \implies p_n \mbox { is odd } ) \\
P(1) & = & (1 \ge 2 \implies 2 \mbox { is odd }) \\
\mbox{ Since } (1 \ge 2) & &\mbox { is false } \\
\mbox{ and } ( 0 \implies 1) & & \mbox{ is true } \\
\therefore 2 & & \mbox{ is odd } \\
\end{eqnarray*}
First of all, the above argument has devolved into nonsense. First of all,
is our $P(n)$ really a statement about all primes. Do we know, for example,
that there really is a $p_{42}$ in the list? What about $p_{14072079482528}$ ?
That index is the national debt as of 11:15:24 pm GMT on 30jan11.
Much more interesting than the national debt is a theorem that there are
really infinitely many primes. And we follow Euclid to prove this by
contradiction.
\begin{itemize}
\item Suppose there are only finetely many primes.
\item Name them $p_1, p_2, ..., p_n $.
\item Take their product $ N = p_1 p_2 ... p_n $
\item Add 1 and consider the number $N+1$.
\item It is clearly not in the list of all primes.
\item And it is not divisible my any of the primes because, if it were, then
$ \frac{N + 1}{p_k} = \frac{p_1p_2...p_n}{p_k} + \frac{1}{p_k} $
\item Which is a sum of a whole number plus a proper fraction, and so not whole.
\item So it is a composite number, itself the product of primes.
\item Hence we arrive at a contradiction. $N+1$ cannot by neither a prime nor
not a prime.
\item Done
\end{itemize}
The following is the most important part of this lesson.
\section{Fundamental Theorem of Arithmetic a.k.a. Prime Decomposition Theorem}
In the previous argument we used the \textit{fundamental theorem of arithmetic},
that every number is either a prime or a product of primes. Curiously, we cannot
prove this theorem without induction. In fact, we have to use a seemingly
stronger version of the Axiom, called \textit{ Axiom of Strong Induction}.
In words, this says that if there is a first natural number for which a
proposition $P(n)$ holds, and thereafter, $P(k)$ holds for all numbers
between that first and the present one (without gaps !) then $P(n)$ holds
for all natural numbers.
\textbf{Principle of Strong Induction}
\begin{eqnarray*}
\mbox{If } (\exists n_0)(n=n_0 &\implies& P(n)) \\
\mbox{and } & & (\forall n > n_0)( n_0 < k < n \implies P(k) ) \\
\mbox{then } (\forall n > n_0)( P(n)) & & \mbox{ holds true. } \\
\end{eqnarray*}
\subsection{Proof of the FTA by strong induction}
The textbook has several examples of strong indction. But this is the only
one you really need to remember forever as a legacy of your having passed
MA348. We shall give a conversational proof. You should turn it into a
set of steps in your Journal.
Obviously, we start with $n_0 = 2$ because $1$ is not a prime, nor a composite.
Question 5. Do you detect an error in an earlier statement in this lesson?
And, is $2$ a prime or a product of primes? Yes. So now, take a deep breath,
we may assume that all numbers from 3 to $n-1$ are either primes or products
of primes. How about $n$? If it is a prime, we're done. If it is not a prime,
it must be the product of two numbers, neither equal to 1. Explicitly,
$ n = ab$ for some numbers less than $n$. We apply the strong induction
hypothesis. Both $a$ and $b$ are primes or products of primes. So their
product is again a product of primes. Basta!
Not so fast. Do both $a$ and $b$ satisfy the hypotheses of the strong induction?
Are both of them necessarily bigger than 2 and less than $n$? Mebbe we have
to tighten up the argument.
Question 6. Fix the gap in the argument above to take care of the case that either or
both of $a=2$ and $b=2$.
\subsection{Housekeeping}
Often, we want to express the prime factorization of a number in an orderly
manner, using unique primes, in order:
$(\forall n)(\exists m, e_1, e_2, ..., e_m, p_1 < p_2 < ... < p_m
\mbox{ primes })( n = p_1^{e_1} p_2^{e_2} .... p_m^{e_m} ) $
\section{Pay Day !}
Regardless of how D'Angelo-West prove their theorems, or you might be inclined
to solve a problem "as in the book", you \textbf{should} attempt to prove
everything using the \textit{ Prime Factorization Theorem}, in either of its
formulation.
In this course, you should apply the Prime Factorization
Theorem (PFT) whenever possible, because this among the central theorems
in three of the remaining lessons of the Discrete Math half of the course.
Solutions to homework problems that do not do this, but instead copy the
methods of some problems in the textbook, will receive only partial credit.
\subsection{Another look at Strong Induction}
There is a corollary of the PFT which says that the prime factorization is
unique up to order. You may amuse yourself by reading D'Angelo-West's proof.
It is an elegant application of induction.
Finally, you might wonder, is "strong" induction really stronger that just
plain garden variety induction? The theorem seems to have a much more demanding
hypothesis to check. In a logic course, such as MA414, or from Google, you'll
see that the two principles of induction are logically equivalent. So, use one
or the other, whichever works.
\end{document}
 Caution:
This commentary on D'Angelo-West was written
for online Netmath students who (1) had to purchase the textbook,
and (2), were far less mathematically prepared than the the current students
at Illinois. Therefore, it took a very low-level approach, but required
careful reading of the text. So, there is a different emphasis here,
which will be developed in the lectures. I will write this in blue.
Caution:
This commentary on D'Angelo-West was written
for online Netmath students who (1) had to purchase the textbook,
and (2), were far less mathematically prepared than the the current students
at Illinois. Therefore, it took a very low-level approach, but required
careful reading of the text. So, there is a different emphasis here,
which will be developed in the lectures. I will write this in blue. 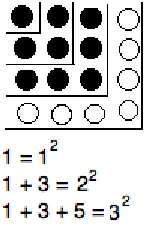 Question 1. State the theorem correctly in your own words.
In that case, you won't mind seeing a rigorous proof.
\begin{itemize}
\item For $ n=1$, it is the sum of the first odd number and is a square.
\item And $ n^2 + (2(n+1) -1) = n^2 + (2n +1 ) = (n+1)^2
\item Done!
\end{itemize}
Done what? \textbf{This is NOT a proof!} It is a fragment of a proof.
Indeed, it is the heart of a proof, but, as it stands, it doesn't
even make sense.
Question 2. List the chief faults of this "proof".
Here is a formal proof:
\begin{eqnarray*}
\mbox{Let } P(n)& = & (\sum_{k=1}^n (2k-1) = n^2) \\
P(1) & = & (\sum_{k=1}^1 (2k-1) = 2-1 = 1 = 1^2) \mbox{ half done} \\
P(n) & = & (\sum_{k=1}^n (2k-1) = n^2) \mbox{ hypothesis, so use it}\\
\mbox{ Calculate } \sum_{k=1}^{n+1} (2k-1) & = & \sum_{k=1}^{n} (2k-1) + (2n+1) \\
&=& P(n) + (2n+1) = n^2 + 2n+1 + 1 = (n+1)^2\\
\therefore & & P(n+1) \\
\end{eqnarray*}
Question 3. Where is the hypothesis used?
Now were done, because $P(1)$ holds and $P(n) \implies P(n+1)$ is true.
\subsection{Sermon}
So what's so difficult here? Some advice on induction problems:
\begin{enumerate}
\item Recognize the problem as being one amenable to finite induction.
\item Analyze the problem and formulate a conjecture (=tentative theorem)..
\item Test your conjectur for $n=1,2,3,4$.
\item Develop a strategy of proof, and compose one.
\item Check your work. What did you leave out?
\end{enumerate}
Here fit 100 practice problems. Put a couple simple ones into your Journal.
As you will notice when looking through the problems given in the D'Angelo-West,
they are either uninteresting, like the one above, or very obscure and difficult. For our purposes, you need to know how use the principle of induction, and to
uynderstand the difference between simple induction and so-called \textit{strong induction}
Question 1. State the theorem correctly in your own words.
In that case, you won't mind seeing a rigorous proof.
\begin{itemize}
\item For $ n=1$, it is the sum of the first odd number and is a square.
\item And $ n^2 + (2(n+1) -1) = n^2 + (2n +1 ) = (n+1)^2
\item Done!
\end{itemize}
Done what? \textbf{This is NOT a proof!} It is a fragment of a proof.
Indeed, it is the heart of a proof, but, as it stands, it doesn't
even make sense.
Question 2. List the chief faults of this "proof".
Here is a formal proof:
\begin{eqnarray*}
\mbox{Let } P(n)& = & (\sum_{k=1}^n (2k-1) = n^2) \\
P(1) & = & (\sum_{k=1}^1 (2k-1) = 2-1 = 1 = 1^2) \mbox{ half done} \\
P(n) & = & (\sum_{k=1}^n (2k-1) = n^2) \mbox{ hypothesis, so use it}\\
\mbox{ Calculate } \sum_{k=1}^{n+1} (2k-1) & = & \sum_{k=1}^{n} (2k-1) + (2n+1) \\
&=& P(n) + (2n+1) = n^2 + 2n+1 + 1 = (n+1)^2\\
\therefore & & P(n+1) \\
\end{eqnarray*}
Question 3. Where is the hypothesis used?
Now were done, because $P(1)$ holds and $P(n) \implies P(n+1)$ is true.
\subsection{Sermon}
So what's so difficult here? Some advice on induction problems:
\begin{enumerate}
\item Recognize the problem as being one amenable to finite induction.
\item Analyze the problem and formulate a conjecture (=tentative theorem)..
\item Test your conjectur for $n=1,2,3,4$.
\item Develop a strategy of proof, and compose one.
\item Check your work. What did you leave out?
\end{enumerate}
Here fit 100 practice problems. Put a couple simple ones into your Journal.
As you will notice when looking through the problems given in the D'Angelo-West,
they are either uninteresting, like the one above, or very obscure and difficult. For our purposes, you need to know how use the principle of induction, and to
uynderstand the difference between simple induction and so-called \textit{strong induction}