Vector Prerequisites for this Course
6jun10\begin{document} \maketitle
 \section{Introduction}
\begin{eqnarray*}
r(A+B) &=& r( (x_A,y_A)+(x_B,y_B) ) \\
&=& r (x_A + x_B, y_A +y_B) \\
& =& ( r(x_A + x_B), r(y_A +y_B) ) \\
&=& ( rx_A + rx_B , ry_A + ry_B ) \ \mbox{distributive law for reals} \\
&=& ( rx_A , ry_A) + (rx_B , ry_B) \\
&=& ( r(x_A , y_A) + r(x_B , y_B) \\
&=& (rA + rB) \\
\end{eqnarray*}
Do you understand what is written above?
To test that you do know how to work with vectors in the plane you need to
read $\S\S$ 1.1-1.6 of Tondeur's text. It's only 7 pages, but you'll need
a pad of paper and a pencil to work your way through it. And, if you have
any difficulty solving the six exercises you should contact your mentor
immediately and consult about remediation you may require to take this course.
What follows here is no substitute for the above. Nor is it a self-contained
review of vector geometry in the plane. It can serve as a very brief review
of the subject as it will be needed in this course. And, more importantly,
it introduces a slightly different slant on this subject than in the book.
If you are easily confused by studying two slightly different treatments of the
same mathematical subject, then you should stick to one or the other. But, if
you plan on reaching a college level understanding of advanced geometry, you
will appreciate complementary expositions. And, in this case, you might also
scour the web for yet different approaches. Contrary to what you might have
been taught in high school, geometry is not a dry, dogmatic and mummified
science. On the contrary, developing definite preferences and opinions is just
as valid here as in any field that requires thought.
\section{Coordinates}
In high school you learned the correspondence between pairs of numbers
and points in a coordinate plane, and how curves in the plane can be
described by equations in the coordinates of its points.
By $P=(x,y)$ or $P=(p_1,p_2)$ and much
more rarely, by $P=(P_x, P_y)=(x_P,y_P)$,
we mean the point located $x$ units to the
right or left of the $y-axis$ and $y$ units above or below the $x-axis$;
or, more precisely, $P$ is the intersection of the two lines with equations
$x = p_1$ and $y=p_2$; and much more rarely, that $P_x=x_P$ is the point on
the horizontal number-line that $P$ projects to vertically,
and $P_y=y_P$ is the point on the vertical number-line that $P$ projects to
horizontally. Whichever way an author might prefer to write this, the
third idea is that "a geometric point \textit{has} two coordinate", not
that "a geometric point can be found by \textit{plotting} two coordinates."
You must transcend the latter idea in favor of the former.
Already you see the same mathematical object, a pair of real numbers,
can have several different geometrical meanings depending on how we
want to think of the coordinates of a point. By the way, you do remember
that the phrase ``the line $x=p_1$" refers to $\{(x,y) : x=p_1\}$.
\section{Vectors}
In college you learned that ordered pairs of numbers could be added,
subtracted, multiplied by a scalar, and satify certain rules, such
as the distributive law, to form what was called a \textit{vector field}.
The geometrical interpretation of a vector also came in a, perhaps
bewildering, variety of forms.
\subsection{Arrows}
A directed line segment, $\overline{AB}$, with its "tail" at $A$
and its "head" at $B$, is associated with the ordered pair $B-A$. For
example, if $A=(1,2)$ and $B=(3,4)$ then $B-A=(2,2)$. Such an object
is more precisely called a \textit{displacement vector} because it
is calculated in terms of having displaced $A$ to $B$.
Now, if you move $A \mapsto A' = A+D$ and $B \mapsto B'= B+D $ then
the displacment vector, $\overline{A'B'}$ has exactly the same
coordinates as $\overline{AB}$ because, as you can check,
\begin{eqnarray*}
B' - A' &=& B - A . \\
\end{eqnarray*}
That is the meaning of the definition you learned in college, that a
vector is an equivalence class of arrows all or which are parallel and
oriented in the same way as any one of them.
So now an ordered pair, say $(2,2)$ as in our example above, has two
meanings: point and vector. How are these related? The Cartesian plane
has a very distinguished point, called the \textit{origin}, $O=(0,0)$.
If the origin is displaced by the vector $(2,2)$ then it ends up at
the point $(2,2)$. And \textit{vice versa},
every point, for example $D=(-42, \pi/2)$,
corresponds to the displacement $\overline{OD}$ of the origin to
itself. And this vector has the same coordinates (or components, as some
prefer) as the point.
Some elementary expositions of this topic develop a bizarre collection of
unnecessary notation in a misguided attempt to help the student keep these
distinctions clearly in their head.
I'm sure you've seen the little arrows over the letters, or obtrusively
thick bold face type for vectors.
We shall not do so. In fact, we will even give up the
unnecessary effort of writing $\overline{AB}$ when $B-A$ specifies
exactly the same vector.
Which meaning is meant is evident from the context of its usage. If we
had to write every instance of the English word "set" differently,
depending on whether it is used as a verb, noun, adjective or interjection,
even fewer children would learn how to spell than already do. By the way,
can you use all four meanings of "set" in the same sentence?
\subsection{Physics}
Another definition you undoubtedly learned in college is that a vector is
anything with a magnitude and direction. The geometrical interpretations of
this is based on polar coordinates of the plane. To define the corresponding
vector, however, requires measuring the distance between two points and the
angle between two rays. Since
this concept is left undefined in affine geometry, we shall not ask you to
remember these concepts now. We shall not need them until a later module
of the course.
\section{Lines}
In high school analytic geometry you learned three, perhaps four formulas,
each of which describes an (infinite) straight line in the plane. The
\textit{point-slope formula}, such as $y=mx+b$, is the one you're most likely
to remember, because it was the first you learned.
Like counting on your fingers, which was still easier for
you in 4th grade than using your newly learned multiplication tables, you'll
fall back on this in a pinch. In algebra you learned the form $ax+by=c$ and
later still, the parametric form. Here are three equivalent forms, without
using coordinates.
\begin{eqnarray*}
\ell_{AB} &= & \{X = A + t(B-A) : t \in \mathbb{R} \} \\
& = & \{X = A(1-t) + tB : t \in \mathbb{R} \} \\
& = & \{X = aA + bB : a,b \in \mathbb{R} \ \and \ a+b=1 \} \\
\end{eqnarray*}
Although they are algebraically equivalent (you should work out a proof
of this assertion first on scratch paper, then enter it into your journal)
they have different geometrical meaning. The first says that the points on
the line through $A$ and $B$ may be reached by first putting you finger on
$A$ and the moving along the displacement vector, $D=B-A$,
both poisitive and negative multiples of $D$. Think of a streetcar.
The second expresses every point on the line as a weighted average of the
positions $A$ and $B$. The weights may be negative, but they must add up
to one. The third formula says this more elegantly, expressing no
prejudices. Of course $a=1-t$ and $b=t$ relates these two. Think of a
teeter-totter. But you must allow a particularly light child to also have
enough helium filled ballons to have a "negative" weight. The position of
the fulcrum of such a teeter-totter is the position described by the
pair of weights $a,b$.
\section{Coordinate Free Geometry}
Although there is always an underlying coordinate system, we shall (almost)
never refer to it. After all, as you recall from high school, one can change
the coordinate system, but the geometrical facts remain the same. In particular
we do not care where the origin is located. It too can move when the coordinate
system is changed.
\subsection{When do we need coordinates?}
We do need the coordinates (a.k.a. components) of vectores to check the rules.
For instance, the \textit{distributive law} would be verified thus. To show that
$ (\forall r \in \mathbb{R} \ \and \ A, B \in \mathbb{R}^2)( r(A+B) = rA + rB ) $
we begin on one side of the equation and appeal to algebra until we get to the
other. You should \textbf{not} work on both sides of an equation you haven't proved yet,
and then work you way to an identity, as you may have been mis-taught to do in
high school. Please read the Advice on proofs elewhere in these notes.
\begin{eqnarray*}
r(A+B) &=& r( (x_A,y_A)+(x_B,y_B) ) \\
&=& r (x_A + x_B, y_A +y_B) \\
& =& ( r(x_A + x_B), r(y_A +y_B) ) \\
&=& ( rx_A + rx_B , ry_A + ry_B ) \ \mbox{distributive law for reals} \\
&=& ( rx_A , ry_A) + (rx_B , ry_B) \\
&=& ( r(x_A , y_A) + r(x_B , y_B) \\
&=& (rA + rB) \\
\end{eqnarray*}
Note that we have identified the step where the distributive law for vectors
is reduced to the distributive law for reals. All the other steps are
applications of the rules for vector algebra.
There will be one other time in the module on Affine Geometry where we
will do something similar to verify the existence and uniqueness of
\textit{barycentric coordinates} in the plane.
\section{Study Guide}
This course is an upper level college math course, and by now you have
surely learned how study mathematics. Nevertheless, since this is the
"remediation lesson" let me remind you of some simple rules of thumb.
Just as every contact hour of a college course requires an average of two
hours of study time, so every lesson in these notes requires an average
of two hours of concetrated study time. Sometimes less, sometimes more.
And by \it{concentrated study time} I do not mean reading the words and
looking at the pictures.
\subsection{How to read a mathematical passage}
Three times. First time through you skim it to see what's there. You
may recognize some items you already know, and other items that make no
sense at all. Mentally tag each sentence. Congratulate yourself on those
that are "obvious" to you, and skip over those that make no sense, .... yet!
The second time you work slowly with pencil and paper at your side. When
sentence takes a moment of thought, write it out on paper. When a sentence
makes an assertion you don't immediately understand why, then work it out on
paper. When you come to one you cannot understand, read it more slowly. If you
cannot fill in the details of assertion, play with some numerical or
graphical examples.
You may have to lay aside a particularly diffiult difficult passage. You
may want to come back to it later, or ask someone else. But don't go
surfing the web. Chances are you won't find anything, and chances are you'll
get distracted by something more interesting. At all events, write down
carefully (in your journal, for example) exactly what you don't understand,
but also what of the question to do understand.
\subsection{How to ask someone else for help}
This too has to be learned. Above all, \textbf{do not} preface your question
by useless phrases like "I am so confused...", "I am probably stupid for not
understanding this but ... ", "You are so clever, I bet you know the answer
right away ...", etc. This just wastes your helper's time. (S)he already
suspects all that, so no need to remind!
Instead, take a dispassionate, diagnostic attitude. Objectify your problem
with the problem. Help your helper to help you!
\subsection{How to ask by email or on a bulleting board.}
Since most of your consulting will be done electronically
in this course it is time to learn that discipline too. Here, avoid such
unhelpful questions like "I don't understand problem 4.2. How can I solve it?"
That kind of a questions is particularly annoying because the only logical
response to
it is to solve it for you. In which case the second question is moot. No need
for you to solve it, the solution is already in your hands. You've learned
nothing, and your helper did you no favor. In this geometry course there are
very few good exercises, and a great deal of text to master before attempting
to solve any one. Therefore, seeing the solution won't help you solve the next
exercise because there rarely are two exercises are "solved exactly the
same way." So, the \textit{drill} is in working out the lesson texts. Solving
an actual exercise is a confirmation that have understand!
So, when asking a question be sure to state the question in your own words.
Don't just copy the phrase from the lesson or exercise set verbatim. By
weritin out your own rephrasing, your astute helper can often tell what your
difficulty really is. Clearing up the misundertanding, and maybe dropping a
little hint, will give you the help you need to solve the problem yourself.
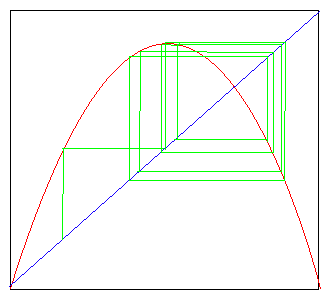
\section{What's with the figure at the top?}
Whenever a figure appears at the top of a lesson, it often is meant to
intrigue and elicit questions. The figure concerns yet another idea that
you acquired in the last geometry course you've taken, which was most
probably a course in analytic geometry in high school. You learned to
\textit{graph} functions like $ y = 3(1-x)x$, by locating the locus of
points that satisfy this equation. So far so good. But then you were taught
to read the function $y=f(x)$ by locating $x$ on the x-axis, rising/falling
to the graph, and then moving right/left to hit $y$ on the y-axis.
All along you were reminded that $f(x) = 3(1-x)x $ is a function
takes real numbers to real numbers. Which real numbers? The one's on the
x-axis or the reals on the y-axis?
A very simple device resolves this mystery, and opens up a tool for
investigating interesting phenomena in the sciences. You place the real
numbers on the diagonal line, and forget about the x-axis and the y-axis
after you've plotted the graph of the function. Locate x on the diagnonal,
draw a vertical to the graph, then a horizontal back to the diagonal real
line, and presto, you have a new way of representing functions. The payoff
is that \textit{feedback}, where the output of the function is
used as the input of the next interation of the function, is easy to visualize.
The moral of this story? Don't be afraid of new ways of looking at old things!
\end{document}
\section{Introduction}
\begin{eqnarray*}
r(A+B) &=& r( (x_A,y_A)+(x_B,y_B) ) \\
&=& r (x_A + x_B, y_A +y_B) \\
& =& ( r(x_A + x_B), r(y_A +y_B) ) \\
&=& ( rx_A + rx_B , ry_A + ry_B ) \ \mbox{distributive law for reals} \\
&=& ( rx_A , ry_A) + (rx_B , ry_B) \\
&=& ( r(x_A , y_A) + r(x_B , y_B) \\
&=& (rA + rB) \\
\end{eqnarray*}
Do you understand what is written above?
To test that you do know how to work with vectors in the plane you need to
read $\S\S$ 1.1-1.6 of Tondeur's text. It's only 7 pages, but you'll need
a pad of paper and a pencil to work your way through it. And, if you have
any difficulty solving the six exercises you should contact your mentor
immediately and consult about remediation you may require to take this course.
What follows here is no substitute for the above. Nor is it a self-contained
review of vector geometry in the plane. It can serve as a very brief review
of the subject as it will be needed in this course. And, more importantly,
it introduces a slightly different slant on this subject than in the book.
If you are easily confused by studying two slightly different treatments of the
same mathematical subject, then you should stick to one or the other. But, if
you plan on reaching a college level understanding of advanced geometry, you
will appreciate complementary expositions. And, in this case, you might also
scour the web for yet different approaches. Contrary to what you might have
been taught in high school, geometry is not a dry, dogmatic and mummified
science. On the contrary, developing definite preferences and opinions is just
as valid here as in any field that requires thought.
\section{Coordinates}
In high school you learned the correspondence between pairs of numbers
and points in a coordinate plane, and how curves in the plane can be
described by equations in the coordinates of its points.
By $P=(x,y)$ or $P=(p_1,p_2)$ and much
more rarely, by $P=(P_x, P_y)=(x_P,y_P)$,
we mean the point located $x$ units to the
right or left of the $y-axis$ and $y$ units above or below the $x-axis$;
or, more precisely, $P$ is the intersection of the two lines with equations
$x = p_1$ and $y=p_2$; and much more rarely, that $P_x=x_P$ is the point on
the horizontal number-line that $P$ projects to vertically,
and $P_y=y_P$ is the point on the vertical number-line that $P$ projects to
horizontally. Whichever way an author might prefer to write this, the
third idea is that "a geometric point \textit{has} two coordinate", not
that "a geometric point can be found by \textit{plotting} two coordinates."
You must transcend the latter idea in favor of the former.
Already you see the same mathematical object, a pair of real numbers,
can have several different geometrical meanings depending on how we
want to think of the coordinates of a point. By the way, you do remember
that the phrase ``the line $x=p_1$" refers to $\{(x,y) : x=p_1\}$.
\section{Vectors}
In college you learned that ordered pairs of numbers could be added,
subtracted, multiplied by a scalar, and satify certain rules, such
as the distributive law, to form what was called a \textit{vector field}.
The geometrical interpretation of a vector also came in a, perhaps
bewildering, variety of forms.
\subsection{Arrows}
A directed line segment, $\overline{AB}$, with its "tail" at $A$
and its "head" at $B$, is associated with the ordered pair $B-A$. For
example, if $A=(1,2)$ and $B=(3,4)$ then $B-A=(2,2)$. Such an object
is more precisely called a \textit{displacement vector} because it
is calculated in terms of having displaced $A$ to $B$.
Now, if you move $A \mapsto A' = A+D$ and $B \mapsto B'= B+D $ then
the displacment vector, $\overline{A'B'}$ has exactly the same
coordinates as $\overline{AB}$ because, as you can check,
\begin{eqnarray*}
B' - A' &=& B - A . \\
\end{eqnarray*}
That is the meaning of the definition you learned in college, that a
vector is an equivalence class of arrows all or which are parallel and
oriented in the same way as any one of them.
So now an ordered pair, say $(2,2)$ as in our example above, has two
meanings: point and vector. How are these related? The Cartesian plane
has a very distinguished point, called the \textit{origin}, $O=(0,0)$.
If the origin is displaced by the vector $(2,2)$ then it ends up at
the point $(2,2)$. And \textit{vice versa},
every point, for example $D=(-42, \pi/2)$,
corresponds to the displacement $\overline{OD}$ of the origin to
itself. And this vector has the same coordinates (or components, as some
prefer) as the point.
Some elementary expositions of this topic develop a bizarre collection of
unnecessary notation in a misguided attempt to help the student keep these
distinctions clearly in their head.
I'm sure you've seen the little arrows over the letters, or obtrusively
thick bold face type for vectors.
We shall not do so. In fact, we will even give up the
unnecessary effort of writing $\overline{AB}$ when $B-A$ specifies
exactly the same vector.
Which meaning is meant is evident from the context of its usage. If we
had to write every instance of the English word "set" differently,
depending on whether it is used as a verb, noun, adjective or interjection,
even fewer children would learn how to spell than already do. By the way,
can you use all four meanings of "set" in the same sentence?
\subsection{Physics}
Another definition you undoubtedly learned in college is that a vector is
anything with a magnitude and direction. The geometrical interpretations of
this is based on polar coordinates of the plane. To define the corresponding
vector, however, requires measuring the distance between two points and the
angle between two rays. Since
this concept is left undefined in affine geometry, we shall not ask you to
remember these concepts now. We shall not need them until a later module
of the course.
\section{Lines}
In high school analytic geometry you learned three, perhaps four formulas,
each of which describes an (infinite) straight line in the plane. The
\textit{point-slope formula}, such as $y=mx+b$, is the one you're most likely
to remember, because it was the first you learned.
Like counting on your fingers, which was still easier for
you in 4th grade than using your newly learned multiplication tables, you'll
fall back on this in a pinch. In algebra you learned the form $ax+by=c$ and
later still, the parametric form. Here are three equivalent forms, without
using coordinates.
\begin{eqnarray*}
\ell_{AB} &= & \{X = A + t(B-A) : t \in \mathbb{R} \} \\
& = & \{X = A(1-t) + tB : t \in \mathbb{R} \} \\
& = & \{X = aA + bB : a,b \in \mathbb{R} \ \and \ a+b=1 \} \\
\end{eqnarray*}
Although they are algebraically equivalent (you should work out a proof
of this assertion first on scratch paper, then enter it into your journal)
they have different geometrical meaning. The first says that the points on
the line through $A$ and $B$ may be reached by first putting you finger on
$A$ and the moving along the displacement vector, $D=B-A$,
both poisitive and negative multiples of $D$. Think of a streetcar.
The second expresses every point on the line as a weighted average of the
positions $A$ and $B$. The weights may be negative, but they must add up
to one. The third formula says this more elegantly, expressing no
prejudices. Of course $a=1-t$ and $b=t$ relates these two. Think of a
teeter-totter. But you must allow a particularly light child to also have
enough helium filled ballons to have a "negative" weight. The position of
the fulcrum of such a teeter-totter is the position described by the
pair of weights $a,b$.
\section{Coordinate Free Geometry}
Although there is always an underlying coordinate system, we shall (almost)
never refer to it. After all, as you recall from high school, one can change
the coordinate system, but the geometrical facts remain the same. In particular
we do not care where the origin is located. It too can move when the coordinate
system is changed.
\subsection{When do we need coordinates?}
We do need the coordinates (a.k.a. components) of vectores to check the rules.
For instance, the \textit{distributive law} would be verified thus. To show that
$ (\forall r \in \mathbb{R} \ \and \ A, B \in \mathbb{R}^2)( r(A+B) = rA + rB ) $
we begin on one side of the equation and appeal to algebra until we get to the
other. You should \textbf{not} work on both sides of an equation you haven't proved yet,
and then work you way to an identity, as you may have been mis-taught to do in
high school. Please read the Advice on proofs elewhere in these notes.
\begin{eqnarray*}
r(A+B) &=& r( (x_A,y_A)+(x_B,y_B) ) \\
&=& r (x_A + x_B, y_A +y_B) \\
& =& ( r(x_A + x_B), r(y_A +y_B) ) \\
&=& ( rx_A + rx_B , ry_A + ry_B ) \ \mbox{distributive law for reals} \\
&=& ( rx_A , ry_A) + (rx_B , ry_B) \\
&=& ( r(x_A , y_A) + r(x_B , y_B) \\
&=& (rA + rB) \\
\end{eqnarray*}
Note that we have identified the step where the distributive law for vectors
is reduced to the distributive law for reals. All the other steps are
applications of the rules for vector algebra.
There will be one other time in the module on Affine Geometry where we
will do something similar to verify the existence and uniqueness of
\textit{barycentric coordinates} in the plane.
\section{Study Guide}
This course is an upper level college math course, and by now you have
surely learned how study mathematics. Nevertheless, since this is the
"remediation lesson" let me remind you of some simple rules of thumb.
Just as every contact hour of a college course requires an average of two
hours of study time, so every lesson in these notes requires an average
of two hours of concetrated study time. Sometimes less, sometimes more.
And by \it{concentrated study time} I do not mean reading the words and
looking at the pictures.
\subsection{How to read a mathematical passage}
Three times. First time through you skim it to see what's there. You
may recognize some items you already know, and other items that make no
sense at all. Mentally tag each sentence. Congratulate yourself on those
that are "obvious" to you, and skip over those that make no sense, .... yet!
The second time you work slowly with pencil and paper at your side. When
sentence takes a moment of thought, write it out on paper. When a sentence
makes an assertion you don't immediately understand why, then work it out on
paper. When you come to one you cannot understand, read it more slowly. If you
cannot fill in the details of assertion, play with some numerical or
graphical examples.
You may have to lay aside a particularly diffiult difficult passage. You
may want to come back to it later, or ask someone else. But don't go
surfing the web. Chances are you won't find anything, and chances are you'll
get distracted by something more interesting. At all events, write down
carefully (in your journal, for example) exactly what you don't understand,
but also what of the question to do understand.
\subsection{How to ask someone else for help}
This too has to be learned. Above all, \textbf{do not} preface your question
by useless phrases like "I am so confused...", "I am probably stupid for not
understanding this but ... ", "You are so clever, I bet you know the answer
right away ...", etc. This just wastes your helper's time. (S)he already
suspects all that, so no need to remind!
Instead, take a dispassionate, diagnostic attitude. Objectify your problem
with the problem. Help your helper to help you!
\subsection{How to ask by email or on a bulleting board.}
Since most of your consulting will be done electronically
in this course it is time to learn that discipline too. Here, avoid such
unhelpful questions like "I don't understand problem 4.2. How can I solve it?"
That kind of a questions is particularly annoying because the only logical
response to
it is to solve it for you. In which case the second question is moot. No need
for you to solve it, the solution is already in your hands. You've learned
nothing, and your helper did you no favor. In this geometry course there are
very few good exercises, and a great deal of text to master before attempting
to solve any one. Therefore, seeing the solution won't help you solve the next
exercise because there rarely are two exercises are "solved exactly the
same way." So, the \textit{drill} is in working out the lesson texts. Solving
an actual exercise is a confirmation that have understand!
So, when asking a question be sure to state the question in your own words.
Don't just copy the phrase from the lesson or exercise set verbatim. By
weritin out your own rephrasing, your astute helper can often tell what your
difficulty really is. Clearing up the misundertanding, and maybe dropping a
little hint, will give you the help you need to solve the problem yourself.
\section{What's with the figure at the top?}
Whenever a figure appears at the top of a lesson, it often is meant to
intrigue and elicit questions. The figure concerns yet another idea that
you acquired in the last geometry course you've taken, which was most
probably a course in analytic geometry in high school. You learned to
\textit{graph} functions like $ y = 3(1-x)x$, by locating the locus of
points that satisfy this equation. So far so good. But then you were taught
to read the function $y=f(x)$ by locating $x$ on the x-axis, rising/falling
to the graph, and then moving right/left to hit $y$ on the y-axis.
All along you were reminded that $f(x) = 3(1-x)x $ is a function
takes real numbers to real numbers. Which real numbers? The one's on the
x-axis or the reals on the y-axis?
A very simple device resolves this mystery, and opens up a tool for
investigating interesting phenomena in the sciences. You place the real
numbers on the diagonal line, and forget about the x-axis and the y-axis
after you've plotted the graph of the function. Locate x on the diagnonal,
draw a vertical to the graph, then a horizontal back to the diagonal real
line, and presto, you have a new way of representing functions. The payoff
is that \textit{feedback}, where the output of the function is
used as the input of the next interation of the function, is easy to visualize.
The moral of this story? Don't be afraid of new ways of looking at old things!
\end{document}