Class Notes on the Proofs of Ceva and Menelaus
21sep10\begin{document} \maketitle
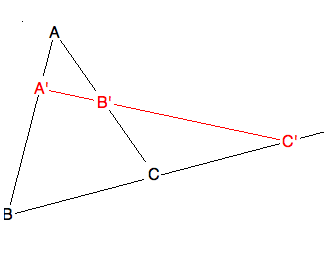This lesson presents the class work in texPad of the four theorems that
establish both Ceva and Menelaus' theorem.
\subsection{Logical form of the Proofs.}
Each, Ceva and Menelaus, has
the logical form $ P \implies (Q \sim R)$, where $P,Q,R$ are
three propositions. The equivalence, in turn, means that
$ (Q \implies R) \and (R \implies Q)$. Thus there are four theorems of the
form $ P \implies (Q \implies R)$. This double implication simplifies to
$ (P \and Q) \implies R$. And that is how we do it.
Morevover, all four have the same first assumption, namely that three
points are given on the sides of a triangle. There is another, tacit
assumtpion, that all of these 6 points are different from each other.
This tacit assumption allows us to do some algebra without fear of dividing
and through by zero, i.e. all shown fractions are real.
\subsection{Technical presentation.}
We decided to present the essence of each proof in real time in class. For
this we used texPad. To keep the exposition short, some necessary justifications,
all due to our "tacit assumption" are left to the student to insert.
\subsection{The four theorems.}
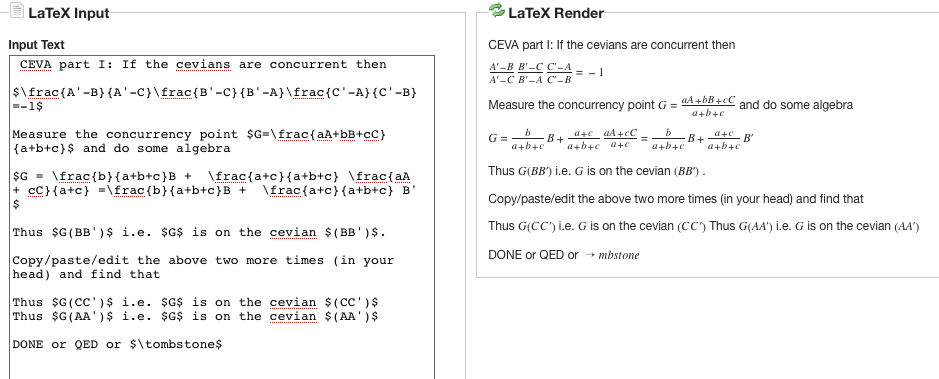
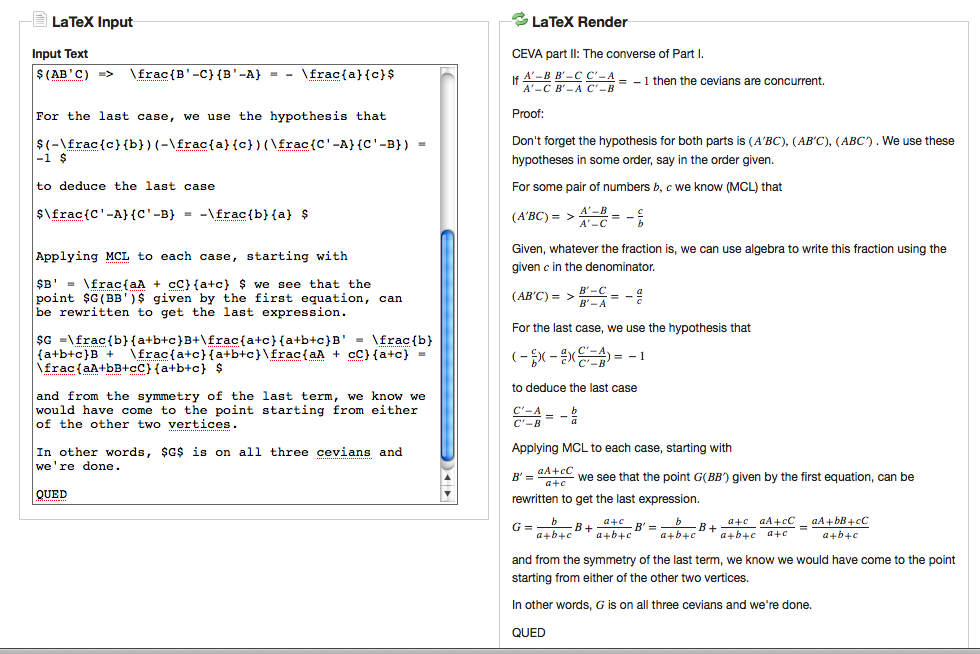
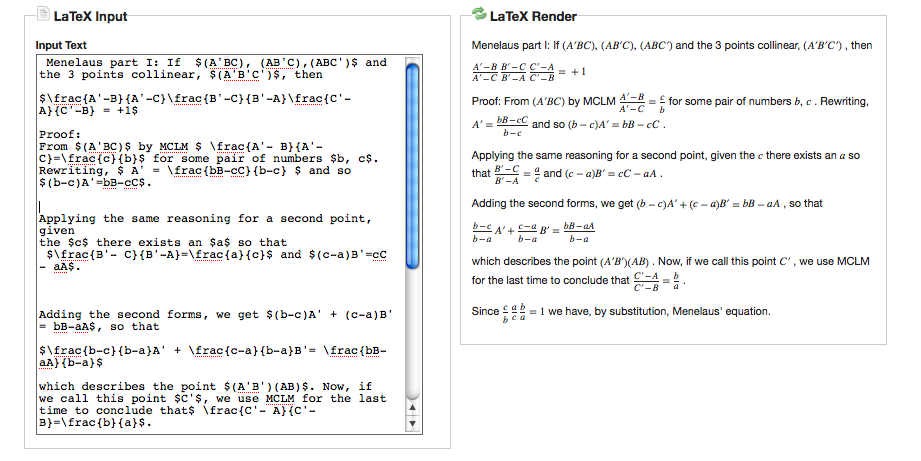
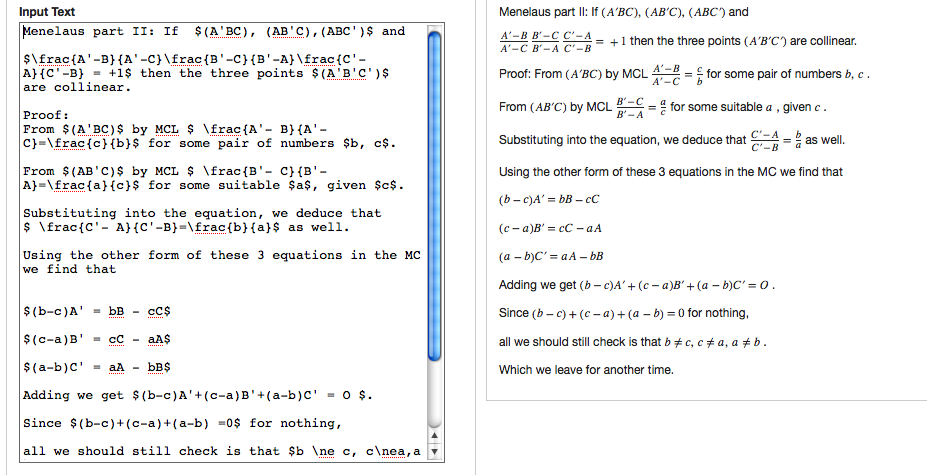\subsection{Discussion.}
You will learn much about proving theorems by comparing these four proofs
with each other, with the proofs for the same theorems in the lessons, and
even with the exposition of the proofs in Tondeur's textbook.
For instance, note the similarity of the two parts for Ceva, compared to the
two parts of Menelaus. Note also the difference. For Menelaus, we made the
two proofs verbatim the same, until one, or the other hypothesis is made to
decide the next step. Opposite conclusions are arrived a.
For Ceva's theorem, the structure of the directions of the equivalence are
not so similarly structured, and so you don't have to pay such close attention in
keeping track of their evolution.
\subsection{The LaTeX Codes.}
For your convenience, here are the text files for the LaTeX code for these
texPad examples.
\end{document}