Solving Levers with the Teeter-Totter Principle.  
9sep10


\begin{document}



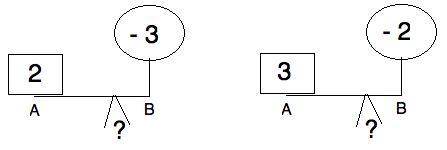\textbf{Question:} Where should the fulcrum be if a weight of $+2$ is
placed at $A$ and a weight of $-3$, a balloon for example, is at $B$?
What if it's $+3, -2$ instead?

\textbf{Solution:}

\subsection{Analyse the known version of this problem}


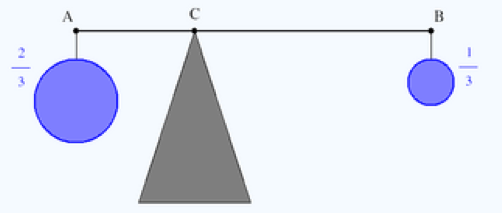In the lesson on barycentric coordinates, 
the weight $a$ and $A$ and $b$ at $B$ become the coefficients in 
 $C = \frac{2A+1B}{2+1} = \frac{2}{3}A + \frac{1}{3} B$. 
The placement of the fulcrum $C$  is obvious. Substitute a variable for a
constant to conjecture the general rule. Let's use a 
$\frac{1}{3} = t$ and write 

$ C =_1 A + t(B-A) =_2 A(1-t) + tB . $ 

Equation 1 places the fulcrum a third of the way from $A$ to $B$. 
Equation 2 identifies this point's barycentric coordinates.
 

\subsection{Generalize and check the validity} 



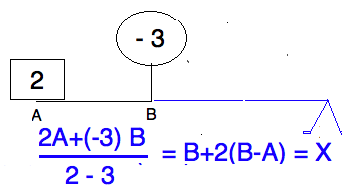Writing $X = \frac{2A + (-3)B}{2-3}$ leads to rewriting 
 rewriting $X = A + 2(B-A)$. This places the fulcrum twice
as far from $B$ making $A$ three times as far from the fulcrum.
The lever equation you learned in high school physics becomes
$ 3 \times 2 = 2 \times 3 $.  


\subsection{Do it again to make sure.}



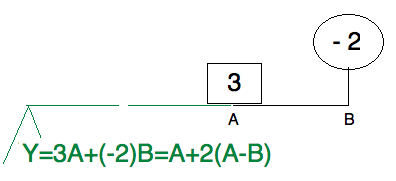Exchanging the weights leads to a surprising result. Following the same 
recipe leads to $Y = 3A + (-2)B = A + 2(A-B) $, which places the fulcrum
on the other side. The lever equation remains the same.


\end{document}