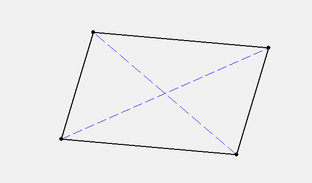
Given four points $A,B,C$, and $D$ in the plane, denote $ABCD$ by the quadrilateral formed by joining $A$ to $B$, $B$ to $C$, $C$ to $D$, and $D$ to $A$. When is such a figure a parallelogram? By definition, when opposite sides are parallel and equal length. In other words, when
$B-A=C-D$ |
$A+C=B+D$ |
$ \frac{A+C}{2}=\frac{B+D}{2} $. |
This proves the
Click here if you didn't quite follow.
Discussion
Which of expressions above are independent of the origin?
The first, $B-A$, is because it is a displacement vector: it represents the change from one point to another in the plane. Conceptually, displacements are not the same thing as locations, because a location is defined relative to a fixed origin and a displacement is defined relative to the two points.
The second expression $A+C$ is not independent of the origin, but the third, $\frac{A+C}{2}$ is. Superficially, the difference appears to be only that we divided the equation by two. However, let’s rewrite the third expression as $\frac{1}{2}A+frac{1}{2}C$. The important thing to notice is that the coefficients $(\frac{1}{2},\frac{1}{2})$ add up to 1, while the coefficients of $A+C$ do not. What this means is that the point a $\frac{1}{2}A+\frac{1}{2}C$ lies on the line through $A$ and $C$; we don’t need a fixed origin because the point is referenced relative to $A$ and $C$.