Exercise 1.7
Let $A,B,C,D$ be an arbitrary quadrilateral (all points are distinct) with
midpoint $M_1$ of side $AB$, $M_2$ of side $BC$, $M_3$ of side $CD$,
$M_4$ of side $DA$.
(a) Prove that $M_1M_2M_3M_4$ is a parallelogram.
(b) Discuss the extreme cases $A = B$ and $A = B = C$ (is the statement of (a) still meaningful
in these cases?).
Sample LaTeX code
\textbf{Problem 1.7.} Let \$A,B,C,D\$ be an arbitrary quadrilateral (all points are distinct) with
midpoint \$M_1\$ of side \$AB\$, \$M_2\$ of side \$BC\$, \$M_3\$ of side \$CD\$,
\$M_4\$ of side \$DA\$.
\vspace{10pt}
(a) Prove that \$M_1M_2M_3M_4\$ is a parallelogram.
\vspace{10pt}
\textbf{Proof.} Answer here.
\vspace{10pt}
(b) Discuss the extreme cases \$A = B\$ and \$A = B = C\$ (is the statement of (a) still meaningful in these cases?).
\vspace{10pt}
\textbf{Answer.}
Exercise 1.8 (paraphrased to simplify notation)
(a) Consider triangle $\triangle ABC$ and midpoints $A', B', C'$
of the sides $BC, CA$, and $AB$ respectively. Show that
$(A'B')$ || $(AB)$, $(B'C')$ || $(BC)$, $(C'A')$ || $(CA)$,
and that $A'-B'=C'-A=\frac{1}{2}(B-A)$.
(b) Let $A',B',C'$ be three non-collinear points.
Find all triangles $\triangle ABC$ for which $\triangle A'B'C'$ is
the triangle on the midpoints of the sides of triangle
$\triangle ABC$.
Sample LaTeX code
\noindent \textbf{Problem 1.8.} (a) Consider triangle \$\triangle ABC\$ and midpoints \$A',B',C'\$
of the sides \$BC,CA\$, and \$AB\$ respectively. Show that
\$(A'B') \| (AB), (B'C') \| (BC), (C'A') \| (CA)\$,
and that
\begin{displaymath}
A'-B'=C'-A=\tfrac{1}{2}(B-A).
\end{displaymath}
\vspace{10pt}
\textbf{Answer.}
Exercise 1.9 (continuing with problem 1.7a)
Consider the same construction carried out also for the
quadrilateral $ACBD$ (watch the order). This results in
a second parallelogram $N_1N_2N_3N_4.$ Note that $N_2=M_2$
and $N_4=M_4$, so that the two resulting parallelograms
have one diagonal in common.
Use KSEG to make a construction of
of this situation and wiggle the given points. What theorem
can you deduce from these experiments?
Sample LaTeX code
\noindent \textbf{Problem 1.9.} Consider the same construction carried out also for the
quadrilateral \$ACBD\$ (watch the order). This results in
a second parallelogram \$N_1N_2N_3N_4.\$ Note that \$N_2=M_2\$
and \$N_4=M_4\$, so that the two resulting parallelograms
have one diagonal in common.
\vspace{10pt}
Use KSEG to make a construction of
of this situation and wiggle the given points. What theorem
can you deduce from these experiments?
\vspace{10pt}
\textbf{Answer.}
Exercise 1.11
Prove that the centroid of a triangle is also the centroid of
the triangle of the midpoints of its sides.
Sample LaTeX code
\noindent \textbf{Problem 1.11.} Prove that the centroid of a triangle is also the centroid of
the triangle of the midpoints of its sides.
\vspace{10pt}
\textbf{Proof.}
Exercise 1.12
Consider Figure 1.10 (a) State and (b) prove the theorem suggested by the figure. (See
link for picture.)
Figure 1.10 consists of a triangle $\triangle ABC$ with medians crossing
at the centroid $G$. The quadrilateral connecting the midpoint
of $AB$ to the midpoint of $BG$ to the midpoint of $CG$ to the midpoint
of $CA$ is drawn into the figure. If you make this construction
in KSEG and wiggle the figure the solution of this problem is easy.
Sample LaTeX code
\noindent \textbf{Problem 1.12.} Consider Figure 1.10 (a) State and (b) prove the theorem suggested by the figure.
\vspace{10pt}
(a) \textbf{Theorem.}
\vspace{10pt}
(b) \emph{Proof.}
Exercise 1.13
Let $ABCD$ be a parallelogram. Prove that the lines joining $A$ to the
midpoints of the opposite sides trisect the diagonal not through $A$.
Sample LaTeX code
\noindent \textbf{Problem 1.13.} Let \$ABCD\$ be a parallelogram. Prove that the lines joining \$A\$ to the
midpoints of the opposite sides trisect the diagonal not through \$A\$.
\vspace{10pt}
\textbf{Proof.}
Exercise 1.16a
Let $ABCD$ be a quadrilateral. Consider the points
$E = \frac{1}{3}(A+2B),\ \ F=\frac{1}{3}(2B+C),\ \ G=\frac{1}{3}(C+2D),\ \ H=\frac{1}{3}(2D+A)$
and prove that $EFGH$ is a parallelogram.
Sample LaTeX code
\textbf{Problem 1.16a.} Let \$ABCD\$ be a quadrilateral. Consider the points
\begin{displaymath}
E = \frac{1}{3}(A+2B),\ \ F=\frac{1}{3}(2B+C),\ \ G=\frac{1}{3}(C+2D),\ \ H=\frac{1}{3}(2D+A)
\end{displaymath}
and prove that \$EFGH\$ is a parallelogram.
\vspace{10pt}
\textbf{Proof.}
Exercise 1.17
Prove that the points with barycentric coordinates $a$ = constant are
the points on the line $\ell$ parallel to $\ell_{BC}$.
Hint: Recall the equation $y=1$ in Cartesian coordinates for the
horizontal line through the point (0,1). In barcentric coordinates
relative to a triangle $\triangle ABC$, and equation like $a=1$ has
an analogous meaning.
Sample LaTeX code
\noindent \textbf{Problem 1.17.} Prove that the points with barycentric coordinates \$a\$ = constant are
the points on the line \$\ell\$ parallel to \$\ell_{BC}\$.
\vspace{10pt}
\textbf{Proof.}
Exercise 1.18 Paint Mixing Problem
Let $A$ be the color red, $B$ the color blue, $C$ the color yellow. If one
mixes $a$ quarts of red paint with $b$ quarts of blue paint and $c$ quarts
of yellow paint, one gets $a+b+c$ quarts of paint of color defined by
the formula
$\frac{1}{a+b+c}(aA+bB+cC)$.
E.g. for $a=b=\frac{1}{2}$ but $c=0$ the result is one quart of purple paint.
For $a=0$ but $b=c=\frac{1}{2}$ the result is one quart of green paint.
Mix one quart of paint of color $\frac{1}{6}(A+2B+3C)$ with an unknown quantity
of paint composed of a mixture of only two colors. This results in
an unknown quantity of mixed paint of color $\frac{1}{5}(2A+2B+C)$. Determine all
the unknown quantities and color.
Hint: This is one of the most impressive problems in Tondeur's text.
The hardest part is to unravel the meaning of the statement of the
problem. Once you have that, the rest is some simple algebra. The
clue to the solution is to notice that the three formulas all look like
the barycentric coordinates of points in the plane relative to a
triangle $\triangle ABC$. Interpret the problem in these geometrical terms, do some
experiments with KSEG, and you will experience the pleasure of solving
a hard mathematical problem.
Sample LaTeX code
\noindent \textbf{Problem 1.18.} Let \$A\$ be the color red, \$B\$ the color blue, \$C\$ the color yellow. If one
mixes \$a\$ quarts of red paint with \$b\$ quarts of blue paint and \$c\$ quarts
of yellow paint, one gets \$a+b+c\$ quarts of paint of color defined by
the formula
\begin{displaymath}
\frac{1}{a+b+c}(aA+bB+cC).
\end{displaymath}
\vspace{10pt}
\noindent Mix one quart of paint of color \$\frac{1}{6}(A+2B+3C)\$ with an unknown quantity
of paint composed of a mixture of only two colors. This results in
an unknown quantity of mixed paint of color \$\frac{1}{5}(2A+2B+C)\$. Determine all
the unknown quantities and color.
\vspace{12pt}
\textbf{Answer.}
Exercise 1.20
Let $(A A'),(B B'),(C C')$ be lines concurring in $G$, as in Ceva's theorem. Prove the following identity
$\frac{G-A}{A'-A}\ +\ \frac{G-B}{B'-B}\ +\ \frac{G-C}{C'-C}\ =\ 2$
Hint: This problem takes some thought. In the statement the lines in
question are cevians, the primed point being on the opposite side. $G$ is
their common intersection. The clue is the Main Collinearity Lemma in the
class notes.
Sample LaTeX code
\noindent \textbf{Problem 1.20.} Let \$(A A'),(B B'),(C C')\$ be lines concurring in \$G\$, as in Ceva's theorem.
Prove the following identity
\begin{displaymath}
\frac{G-A}{A'-A}+\frac{G-B}{B'-B}+\frac{G-C}{C'-C}=2.
\end{displaymath}
\vspace{10pt}
\textbf{Proof.}
Exercise 1.21
Let $(A A'),(B B'),(C C')$ be lines concurring in $G$, as in Ceva's theorem. For which $G$ inside $\triangle ABC$ is the number
$\frac{G-A}{G-A'}\ +\ \frac{G-B}{G-B'}\ +\ \frac{G-C}{G-C'}\ =\ x$
a maximum? (Note that each of these numbers is negative.)
Sample LaTeX code
\noindent \textbf{Problem 1.21.} Let \$(A A'),(B B'),(C C')\$ be lines concurring in \$G\$, as in Ceva's theorem.
For which \$G\$ inside \$\triangle ABC\$ is the number
\begin{displaymath}
\frac{G-A}{G-A'}+\frac{G-B}{G-B'}+\frac{G-C}{G-C'}=x
\end{displaymath}
a maximum? (Note that each of these numbers is negative.)
\vspace{10pt}
\textbf{Proof.}
Exercise 1.22
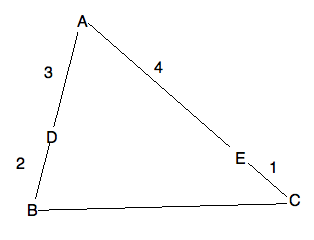
Consider the indicated ratios in Figure 1.14 (described below). Determine
$X$ as a point of $(CD)$ and $(BE)$, i.e. $X=(CD)(BE)$, by applying Menelaus'
theorem.
Figure: On $\triangle ABC$, the point $D$ lies on side $AB$ with the numbers
3 and 2 printed along $AD$ and $DB$ respectively. These indicate a ratio, not
absolute distances. (Review the difference between proportions of
collinear line segments and measuring distances in the class notes.)
The numbers 4 and 1 are printed along $AE$ and $EC$ respectively.
Sample LaTeX code
\noindent \textbf{Problem 1.22.} Consider the indicated ratios in Figure 1.14. Determine
\$X\$ as a point of \$(CD)\$ and \$(BE)\$, i.e. \$X=(CD)(BE)\$, by applying Menelaus'
theorem.
\vspace{10pt}
\textbf{Proof.}
