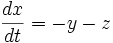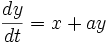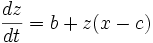User Documentation for Dyn.py

This document describes how to operate and modify the Dynamical System Machine, dyn.py.

Controls

Button Zero - (or Left Click) - Pressing this button switches to the next dynamical system.
Button One - (or Middle Click) - Pressing this button changes to the particle's perspective.
Button Two - (or Right Click) - Pressing and HOLDING this button allows you to rotate and translate the system by moving the wand appropriately. Similar to cosmos.py.
Joystick - The joystick also translates the system.

Adding More Dynamical Systems

Dyn.py is written such that new dynamical systems can easily be added to code the without prior programming experience. Here is a transformation from a system of differential equations to the proper code to be added to dyn.py.

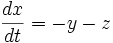
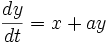
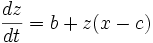
Let a=0.2, b=0.2, c=4.7
First, use Gauss - Sidel to transform the differential equations:

dx = (-y - z)*dt
dy = (x + 0.2*y)*dt
dz = (0.2 + z*(x-4.7))*dt

============================

h is step value

x' = (-y - z)*h + x
y' = (x + 0.2*y)*h + y
z' = (0.2 + z*(x-4.7))*h + z

=============================

Drop the equations into this format:

xRos = lambda x,y,z,h: -(y+z)*h + x
yRos = lambda x,y,z,h: (x + .2*y)*h + y
zRos = lambda x,y,z,h:(0.2+z*(x-4.7))*h + z
hRos = 0.04

Then you add these lines into the createFunctions function and add the names of the equations and constant (xRos, yRos, zRos, hRos) to their respective arrays (xEqs, yEqs, zEqs, hs). For those who are curious, the lambda keyword creates an anonymous function for that equation. We then assign the created function a name, like xRos to refer to it later. Below is a before and after snapshot of adding the Rossler system to dyn.py.

Before

def createFunctions():
#Lorenz
xLor = lambda x,y,z,h:(10*y - 10*x)*h + x
yLor = lambda x,y,z,h:(28*x - y - x*z)*h + y
zLor = lambda x,y,z,h:(-(2.66667)*z + x*y)*h + z
hLor = .004

xeqs = (xLor)
yeqs = (yLor)
zeqs = (zLor)
hs = (hLor)
return (xeqs, yeqs, zeqs, hs)

After

def createFunctions():
#Lorenz
xLor = lambda x,y,z,h:(10*y - 10*x)*h + x
yLor = lambda x,y,z,h:(28*x - y - x*z)*h + y
zLor = lambda x,y,z,h:(-(2.66667)*z + x*y)*h + z
hLor = .004

#Rossler
xRos = lambda x,y,z,h: -(y+z)*h + x
yRos = lambda x,y,z,h: (x + .2*y)*h + y
zRos = lambda x,y,z,h:(0.2+z*(x-4.7))*h + z
hRos = .04

xeqs = (xLor, xRos)
yeqs = (yLor, yRos)
zeqs = (zLor, zRos)
hs = (hLor, hRos)
return (xeqs, yeqs, zeqs, hs)