Last edited 8may08 by schaber2@uiuc.edu
Find this document at http://cheer.math.edu/reulab/web/schaber2
CFD CUDA: Accessing the power of a GPU for use in 3-D simulations

Abstract
My project focuses on learning how to program the NVIDIA GPU so that it's parallel computation capabilities
might be used to help render graphics in the virtual environments.
Using the fluidsGL program provided in the SDK, I will first separate the
relevant computational code from the graphics handling, by storing the data produced
and then using it to run an animation with a solely graphical program.
After this I will set up a pipe between the computational code and animation code to allow interactivity.
Then replace the pipe with a socket so that the GPU can be used as a member of a Syzygy fleet.
History
While GPU's are engineered mainly to handle, as their name suggests, graphical computations, they are becoming an attractive alternative to general purpose CPU's for some computationally intensive problems. The calculations required for graphics processing lend themselves to parallelism. As such, current GPU's offer the ability to perform massively parallel computations orders of magnitude faster than CPU's. With the future of discrete GPU's uncertain, companies such as NVIDIA are promoting the use of their GPU's for scientific and engineering applications. To this end NVIDIA has developed CUDA, an extension to the C programming language to aid in programming on their GPU's. The ability to harness the parallel computation capabilities of the GPU would allow for several computation-intensive simulations to be run in the CAVE or the CUBE.
Mathematics
The fluidsGL program attempts to solve a two dimensional
Navier-Stokes equation using the method proposed by Jos Stam1 in his
1999 paper. The algorithm makes certain assumptions that result in a solution
that is not completely accurate, but computationally efficient and visually appealing. In the most general sense the Navier-Stokes equation is merely a
statement that momentum is conserved. More specifically, that changes in
momentum in infinitesimal volumes of fluid are simply the sum of dissipative
viscous forces, changes in pressure, gravity, and other forces acting inside
the fluid.
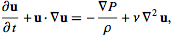
To solve this differential equation exactly would be very difficult so we solve
for (or at least approximate) the solution to each individual term iteratively,
with the notion that these separate terms will superimpose to give a nice
approximation of the actual solution. For each term we update the velocity
field, which is simulated as a grid of discrete points over our domain. It is
here that the GPU has a distinct advantage over a CPU. Each point velocity
needs to be updated individually with the same equation, meaning the
computation is very parallel2.
1. The first term we handle is the addition of an outside
force f. This is by far the easiest as we can just the Euler integration method
i.e. v=f*dt where dt is our (pre-determined and constant) time step.
2. The second step uses the updated velocity field to
account for advection. To this end we assume that the velocity at any point is
equal to the velocity the particle at that point had a time step ago.
3. Again using the updated velocity field we now solve
for the effect of diffusion. Since the fluidsGL program is a torus the
boundary is periodic meaning this step can be solved using a FFT which makes the complicated differentiation a simple multiplication.
4. Finally we take the inverse Fast Fourier Transform to
project our velocity field back onto our 2-D plan.
Operating Instructions
Static Viewer
To make and play a simple pre-generated animation compile
and run fluidsStaticCalc.cu passing in the desired name of the to be
created output file that will contain every tenth frame viewed. Then run fluidsGraphics on any machine with a command line argument of a valid output
file.
Dynamic Viewer
First run fluidsServer port where port
is the port number to listen on, on AH 130-15. Once the server indicates it is
initialized and listening on the given port run fluidsClient IP address port on the remote machine.
Bibliography
1. "Stable Fluids." by Jos Stam link
2. "CUDA/GL Fluid Simulation" by Nolan Goodnight link