Some Logic and Lots of Symbols
7jan11\begin{document} \maketitle
 \section{Symbolic Logic}
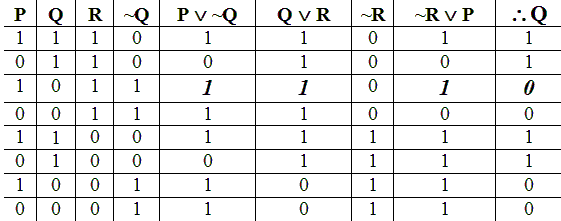
An important prerequisite for this course is the symbolic logic and proof theory
you learned in MA347, MA348 or an equivalent course elsewhere. Consider, for instance,
this sentence an author might preface a problem in the first chapter of a
textbook:
``Coming this early in the text suggests that somehow not being able to supply
the proof, a student is unprepared for the course."
Just what does this mean? Try to reword it by a liberal use of ``if's" and
``then's". Let's abbreviate three sentences by letters standing for
propositions.
\begin{itemize}
\item A = ``Pons Asinorum comes early in the course."
\item B = ``The student is unable to supply the proof."
\item C = ``The student is unprepared for the course."
\end{itemize}
Recall that a \textit{proposition} is a complete sentence (subject and predicate)
which can be determined to be either true of false. Bertrand Russell's example
``The king of France is bald" is an example of a sentence that is not a proposition.
Can you think of some other examples?
The original sentence can now be rephrased in one of two ways:
\begin{itemize}
\item D = ``Given A, if B then C "
\item E = ``If A and B, then C"
\end{itemize}
Recall from MA347, the ``if X then Y" form is called \textit{material implication}
and may be written as ``X => Y". Recall also that the truth table of => is identical to the
truth table of ``not X or Y". We express D in symbolic form thus
D as `` A => (B=>C)". It gives common English mathematical precision.
You should remember from earlier courses how prove that
D and E are equivalent. You can use the rules of the symbolic logic
or truth tables. Do it!
\section{LaTeX, HTML and your Webbrowser}
On this website we use mathematical notation, most of which presents
problems in writing from the keyboard. For example, in the last paragraph, we typed
=> for $\implies$, which resemble each other well enough. ``not X or Y" is a poor
substitute for $ \ \neg X \ \or \ Y $. Still, the keyboard notation remains readable.
And these matters are treated extensively elsewhere in this directory.
Here we list the notation needed to make this and similar document looking
typographically correct on your webbrowser. In the table below, the Javascripts
we use should make the LaTeX term on the left print like the symbol on the right.
But, at least up to August 2010, this works only on certain browsers, like
Firefox and Internet Explorer,
which are able to read a web language called \it{MATHML}.
Other browsers, like Chrome and Safari, cannot do this reliably.
In LaTeX, thus on texWins, the code on the left also prints the symbol
on the right, and does the curly phi correctly.
I you're curious as to why, you can
follows this silly debate among experts on the web.
All versions of Firefox have native MathML support. Possibly up to the
current version, IE still needs the MathML Player Plugin.
(http://www.dessci.com/en/products/mathplayer/). The next version of IE is
supposed to have native support. Both browsers are very easy to download
for free from the web and install on your computer. If the symbols on the
right look wrong, my may have to do this.
\begin{eqnarray*}
\mbox{\wedge} & \wedge \\
\mbox{\and} & \and \\
\mbox{\frac12} & \frac12 \\
\mbox{\ell} & \ell \\
\mbox{\pm} & \pm \\
\mbox{\times} & \times \\
\mbox{\cap} & \cap \\
\mbox{\cup} & \cup \\
\mbox{\vee} & \vee \\
\mbox{\or} & \or \\
\mbox{\and} & \and \\
\mbox{\exists} & \exists \\
\mbox{\forall} & \forall \\
\mbox{\equiv} & \equiv \\
\mbox{\setminus} & \setminus \\
\mbox{\sim} & \sim \\
\mbox{\cong} & \cong \\
\mbox{\neg} & \neg \\
\mbox{\in} & \in \\
\mbox{\notin} & \notin \\
\mbox{\subset} & \subset \\
\mbox{\Rightarrow} & \Rightarrow \\
\mbox{\rightarrow} & \rightarrow \\
\mbox{\copyright} & \copyright \\
\mbox{\sum} & \sum \\
\mbox{\int_0^1 } & \int_0^1 \frac{dt}{t} \\
\mbox{\perp} & \perp \\
\mbox{\S}\ =\ section & \S \\
\mbox{\P}\ =\ paragraph& \P \\
\mbox{\emptyset} & \emptyset \\
\mbox{\bot} & \bot \\
\mbox{\varphi} \ =still\ wrong & \varphi \\
\mbox{\mathbb{N}\} = \ natural\ numbers \ & \mathbb{N} \\
\mbox{\mathbb{Z}\} =\ integers \ & \mathbb{Z} \\
\mbox{\mathbb{Q}\} =\ rationals \ & \mathbb{Q} \\
\mbox{\mathbb{R}\} =\ reals \ & \mathbb{R} \\
\mbox{\mathbb{C}\} =\ complex\ numbers\ & \mathbb{C} \\
\end{eqnarray*}
\end{document}
\section{Symbolic Logic}
An important prerequisite for this course is the symbolic logic and proof theory
you learned in MA347, MA348 or an equivalent course elsewhere. Consider, for instance,
this sentence an author might preface a problem in the first chapter of a
textbook:
``Coming this early in the text suggests that somehow not being able to supply
the proof, a student is unprepared for the course."
Just what does this mean? Try to reword it by a liberal use of ``if's" and
``then's". Let's abbreviate three sentences by letters standing for
propositions.
\begin{itemize}
\item A = ``Pons Asinorum comes early in the course."
\item B = ``The student is unable to supply the proof."
\item C = ``The student is unprepared for the course."
\end{itemize}
Recall that a \textit{proposition} is a complete sentence (subject and predicate)
which can be determined to be either true of false. Bertrand Russell's example
``The king of France is bald" is an example of a sentence that is not a proposition.
Can you think of some other examples?
The original sentence can now be rephrased in one of two ways:
\begin{itemize}
\item D = ``Given A, if B then C "
\item E = ``If A and B, then C"
\end{itemize}
Recall from MA347, the ``if X then Y" form is called \textit{material implication}
and may be written as ``X => Y". Recall also that the truth table of => is identical to the
truth table of ``not X or Y". We express D in symbolic form thus
D as `` A => (B=>C)". It gives common English mathematical precision.
You should remember from earlier courses how prove that
D and E are equivalent. You can use the rules of the symbolic logic
or truth tables. Do it!
\section{LaTeX, HTML and your Webbrowser}
On this website we use mathematical notation, most of which presents
problems in writing from the keyboard. For example, in the last paragraph, we typed
=> for $\implies$, which resemble each other well enough. ``not X or Y" is a poor
substitute for $ \ \neg X \ \or \ Y $. Still, the keyboard notation remains readable.
And these matters are treated extensively elsewhere in this directory.
Here we list the notation needed to make this and similar document looking
typographically correct on your webbrowser. In the table below, the Javascripts
we use should make the LaTeX term on the left print like the symbol on the right.
But, at least up to August 2010, this works only on certain browsers, like
Firefox and Internet Explorer,
which are able to read a web language called \it{MATHML}.
Other browsers, like Chrome and Safari, cannot do this reliably.
In LaTeX, thus on texWins, the code on the left also prints the symbol
on the right, and does the curly phi correctly.
I you're curious as to why, you can
follows this silly debate among experts on the web.
All versions of Firefox have native MathML support. Possibly up to the
current version, IE still needs the MathML Player Plugin.
(http://www.dessci.com/en/products/mathplayer/). The next version of IE is
supposed to have native support. Both browsers are very easy to download
for free from the web and install on your computer. If the symbols on the
right look wrong, my may have to do this.
\begin{eqnarray*}
\mbox{\wedge} & \wedge \\
\mbox{\and} & \and \\
\mbox{\frac12} & \frac12 \\
\mbox{\ell} & \ell \\
\mbox{\pm} & \pm \\
\mbox{\times} & \times \\
\mbox{\cap} & \cap \\
\mbox{\cup} & \cup \\
\mbox{\vee} & \vee \\
\mbox{\or} & \or \\
\mbox{\and} & \and \\
\mbox{\exists} & \exists \\
\mbox{\forall} & \forall \\
\mbox{\equiv} & \equiv \\
\mbox{\setminus} & \setminus \\
\mbox{\sim} & \sim \\
\mbox{\cong} & \cong \\
\mbox{\neg} & \neg \\
\mbox{\in} & \in \\
\mbox{\notin} & \notin \\
\mbox{\subset} & \subset \\
\mbox{\Rightarrow} & \Rightarrow \\
\mbox{\rightarrow} & \rightarrow \\
\mbox{\copyright} & \copyright \\
\mbox{\sum} & \sum \\
\mbox{\int_0^1 } & \int_0^1 \frac{dt}{t} \\
\mbox{\perp} & \perp \\
\mbox{\S}\ =\ section & \S \\
\mbox{\P}\ =\ paragraph& \P \\
\mbox{\emptyset} & \emptyset \\
\mbox{\bot} & \bot \\
\mbox{\varphi} \ =still\ wrong & \varphi \\
\mbox{\mathbb{N}\} = \ natural\ numbers \ & \mathbb{N} \\
\mbox{\mathbb{Z}\} =\ integers \ & \mathbb{Z} \\
\mbox{\mathbb{Q}\} =\ rationals \ & \mathbb{Q} \\
\mbox{\mathbb{R}\} =\ reals \ & \mathbb{R} \\
\mbox{\mathbb{C}\} =\ complex\ numbers\ & \mathbb{C} \\
\end{eqnarray*}
\end{document}