2015 Oct 30

2015 Nov 6

Time for some actual hypergraphics! I've been testing my multivector code with numerical examples to be sure it works, and experimenting in PyOpenGL to get used to the low-level graphics code again, so now it's time to put those together.

I built a series of test applications to make sure the rotors worked, building up to the spinning polybar. After fixing several small errors mostly involving the exponentials I had an animated rotating cube using only geometric algebra (no rotation matrices). I then expanded this to a rotating tribar, then to an n-bar using a custom class.

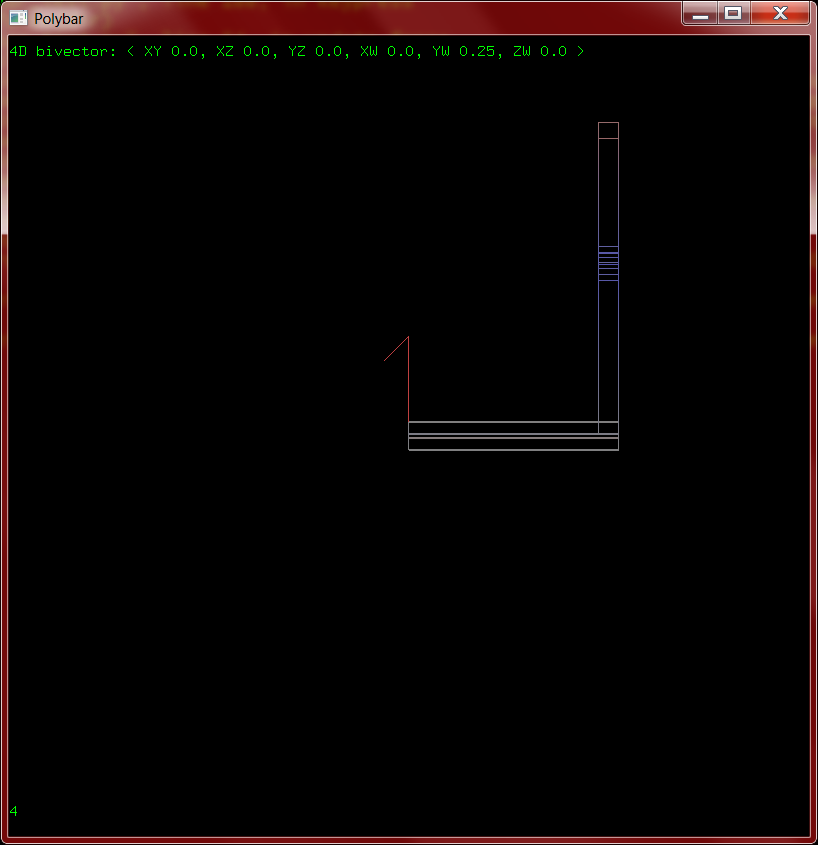
With constant rotations working I also started to implement physics on the polybar class. Linear and angular position are stored as the haplovector and bivector components of a single n-multivector, and likewise for linear and angular velocity. (Momentum might seem the more fundamental quantity, but the moment of inertia calculations are surprisingly expensive to invert, while multiplication is relatively easy.) Every tick the velocity is scalar-multiplied by the elapsed time and added to the position; every frame the vertices are transformed by the position and drawn to the screen.

The code is not particularly efficient, but it works quite well for low numbers of dimensions (the lag only begins to appear above 5 on my machine). Every time the spacebar is pressed, a new random force and position on the bar are chosen (as indicated by the arrow), then applied as an impulse. The bar is anchored at the origin so only the angular momentum changes. In three dimensions the "axis of rotation" (Hodge dual of angular velocity) is drawn as well to make the precession more evident, though this does not generalize well. The ideal would be a good representation of an arbitrary bivector, but for n>3 not all bivectors are 2-blades and thus some cannot be drawn as planes.

2015 Nov 13

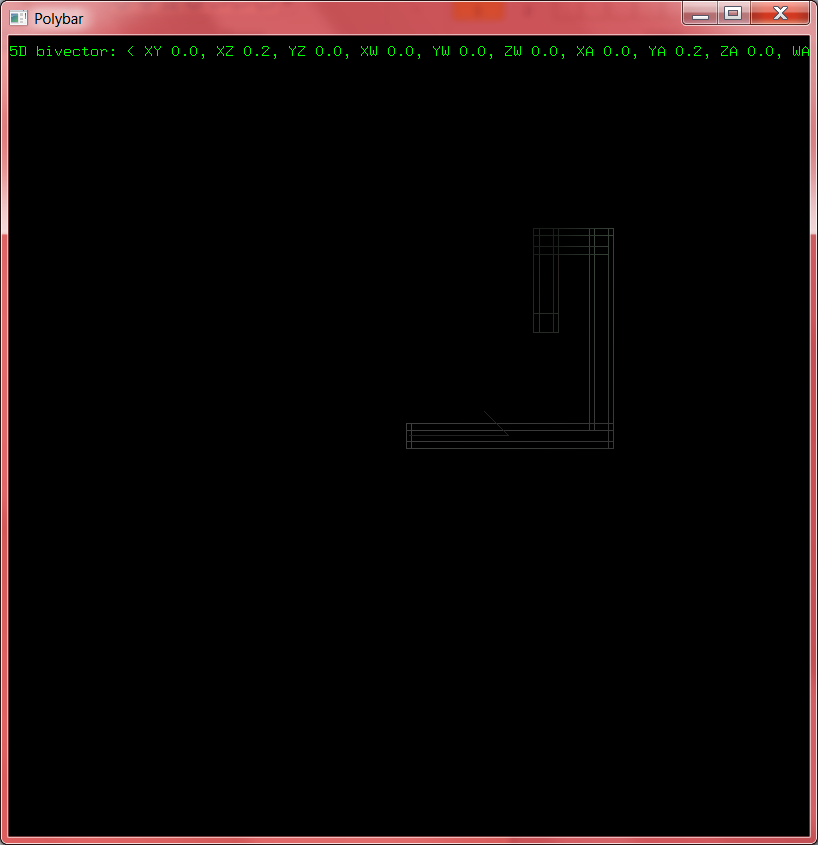
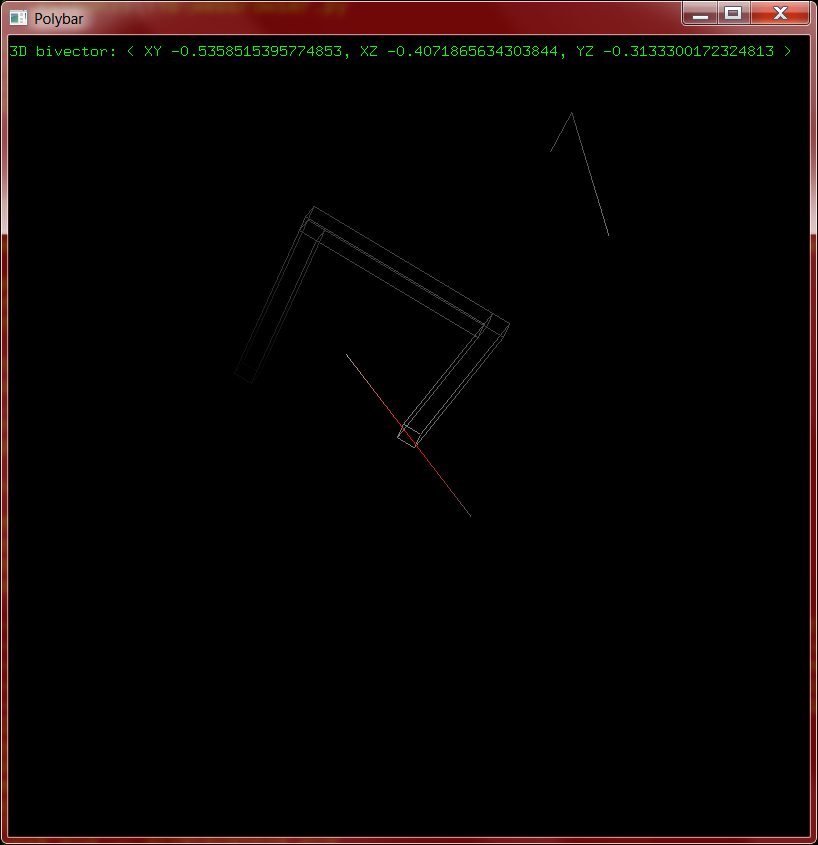
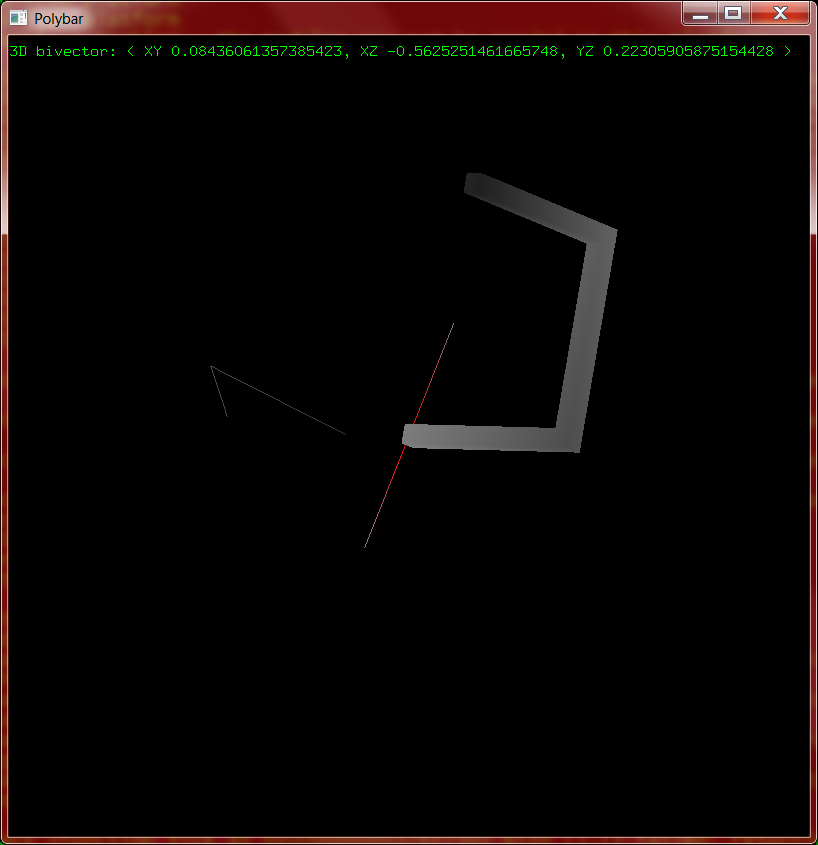
The code I have now works well enough, but it was built as a simple test and grew from there. It's time to refactor this into something more useful. I ripped the polybar class in half, putting the physics simulation aspects (mass, velocity, impulse responses) into solid and the polybar-specific parts into a new subclass. Now that there are multiple classes involved I also made a new polybox class, which is like a polybar but uses actual boxes instead of line segments. It looks cooler but is also far more expensive, as an n-polybox contains n boxes with 2ⁿ vertices each. At anything above three dimensions the lag becomes problematic.

Since the solid class now does more of the behind-the-scenes work, I can start putting bulkier, less elegant but more efficient cases in directly. Getting a single point is a clean and simple interface, but it requires redoing all of the rotor calculations every time. It's now set up to cache as much as possible for the rotations. It does as much of the calculation as it can without using the point itself, separating out the linear displacement and the "left side" and "right side" bivectors for the rotation. Then these values are stored in a dictionary and used for all rotations until something changes.

I also played around with different rendering modes. With the polyboxes it makes sense to talk about faces as well as edges, and changing that part of the renderer is very simple (GL_LINES to GL_QUADS and look up two more vertices). Unfortunately without shading this is much harder to see and understand than the wireframe/line mode, so the default will remain so.

Finally, I made the program significantly easier to run. It requires a fairly modern version of Python (3.5.* or higher) and the awkward PyOpenGL library and dependencies, so installation is not trivial. cx_Freeze and py2exe both have difficulty with the OpenGL components but PyInstaller accepted them all and produces a simple EXE without external dependencies (at least on the machines I have tested).

2015 Nov 20

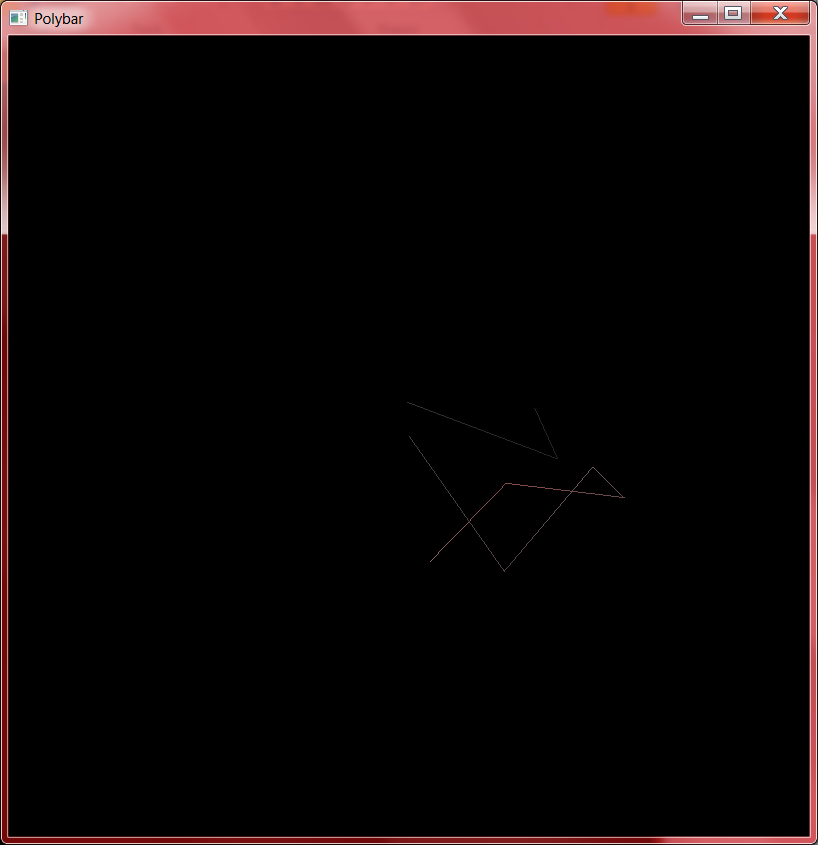
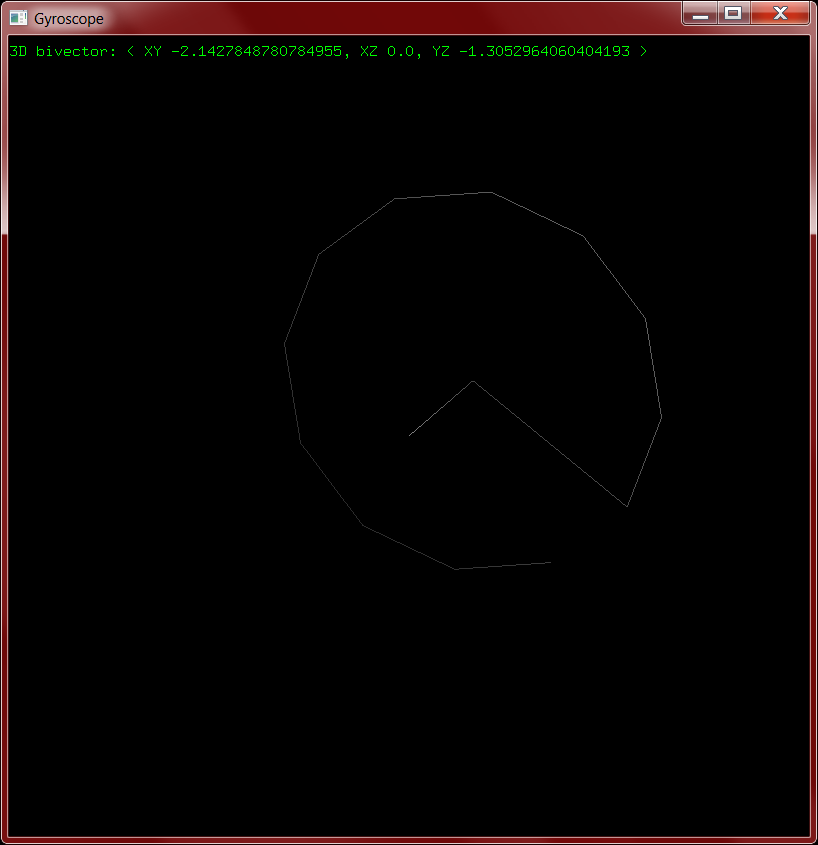
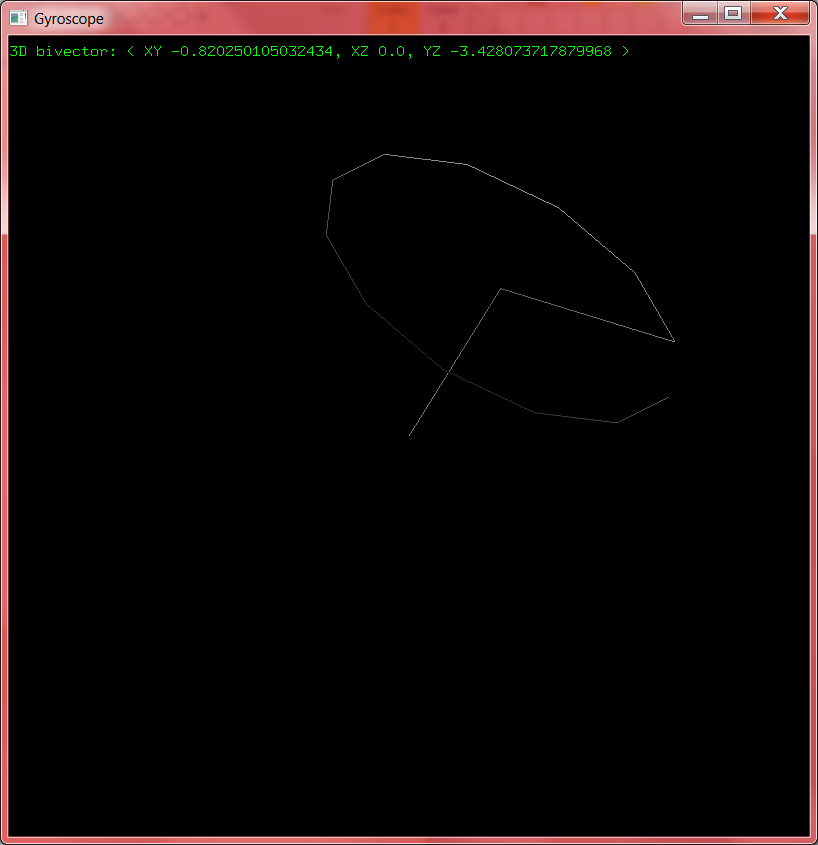
From the solid framework I started building the gyro class, for the simple gyroscope simulation. Precession is one of the clearest applications of "cross products" in three dimensional physics, so showing how it can be calculated with bivectors will help demonstrate their utility even in a three-dimensional world.

Unfortunately, my simple moment of inertia calculations proved insufficient here. The polybar was simulated as a simple pendulum with I=mr². But for a more complicated object like a gyroscope the moment of inertia is different in different planes; I can't just treat it as a scalar.

This was also when I ran into problems with my inner product calculations. Multiplying corresponding elements and taking the sum works for the inner product of two vectors, since each basis vector squares to 1. But the basis bivectors square to -1, so they must be subtracted instead. And strictly speaking I am using the "scalar inner product" (or Hollow Dot product, generally indicated with an empty circle), not the "dot inner product": if there is no scalar component to the product, I return zero instead of the next lowest component.

The first step was to overhaul my inner product routines to calculate from the geometric product rather than taking shortcuts. It makes it significantly slower, but lets me do different types of product: left and right contractions, and the "dot" inner product as well as the "hollow" one. The "dot" is now the default since it's generally the most useful.

2015 Nov 27

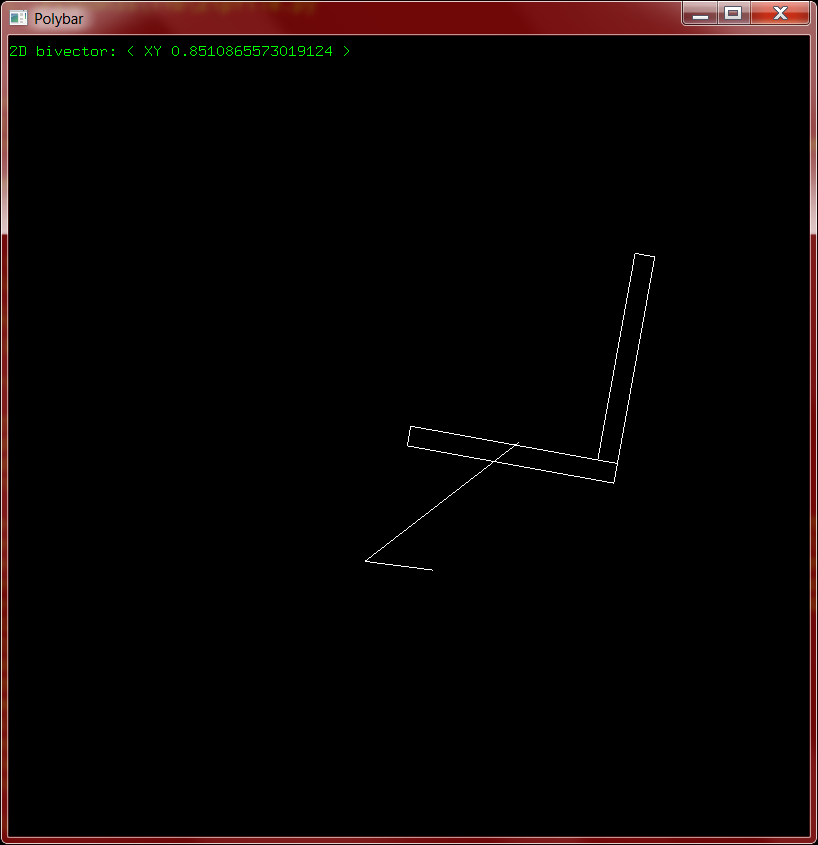
I spent some time over the break working on the gyroscope simulation. Overhauling the moment of inertia calculation for general solids was tedious and difficult, but useful: it now divides the mass evenly between all of the vertices, then projects each into the plane of torque to get the "axial" distance from the center of rotation. This allows for different moments of inertia in different rotational planes.

The next problem was tuning the gyroscope so that it showed some sort of precession. I'm still making a lot of approximations in my simulation, and they add up: if the parameters aren't right the gyro sometimes just falls over or flies out of control. I now have it set up so that the axis very clearly changes over time, but the rotation of the gyroscope itself is also perceptible.

2015 Dec 4

The gyroscope is working pretty well, and I think improving the polybar now will be a better use of time. I started implementing a method to control the forces and locations to move the bar more precisely: press a number to select a direction for the force, then another to select its location. (0 means one unit on the X axis, 1 means one unit on the Y, 2 on the Z, and so on.) This makes it easier to create specific types of rotations to study, such as the 'isoclinics' in four dimensions (combination of two rotations that do not interact, through the same angle; there's no analogue in three dimensions or lower).

I've also started putting my work down in LaTeX for a prototype of my presentation; the current version is in mathwriteup1.tex for perusal.