Last edited 08Dec2014 by jpekosh2@illinois.edu
Find this document at http://new.math.uiuc.edu/math198/jpekosh2
Go to Index
Asteroids: Lagrange Points and the Circular Restricted 3-Body Problem - Fall 2014
By: Jeffrey Pekosh for Math198 class.
Abstract
This project seeks to demonstrate the physics of the circular restricted
3-body problem and illustrate the phenomenon of Lagrange points which
are an important concept both in astronomy and in space mission planning.
It will utilize VPython to simulate and illustrate a dynamical system
and allow the user to interact with and view the simulation and gain some
physical intuition about how these physical systems operate.
About Lagrange Points and The Circular Restricted 3-Body Problem:
TO BE ADDED.
Return to Index.
Progress Reports:
Update Wk9 10/23: Added abstract to page. Created a basic circular restricted 3-body simulation in VPython using Euler integration. Next I need to work on expanding it to allow an arbritrary number of objects and implement a better integration method.
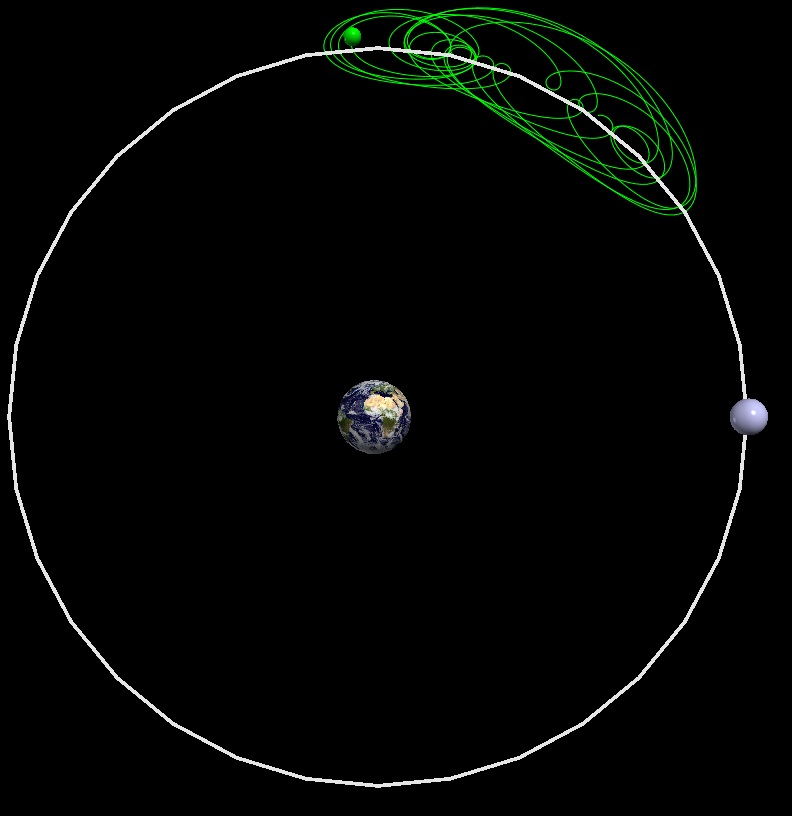
Update Wk10 11/1: Upgraded the VPython simulation to use Runge-Kutta integration for greater accuracy, and managed to allow the program to simulate more than one object easily, given that some initial conditions are provided or generated by the program.
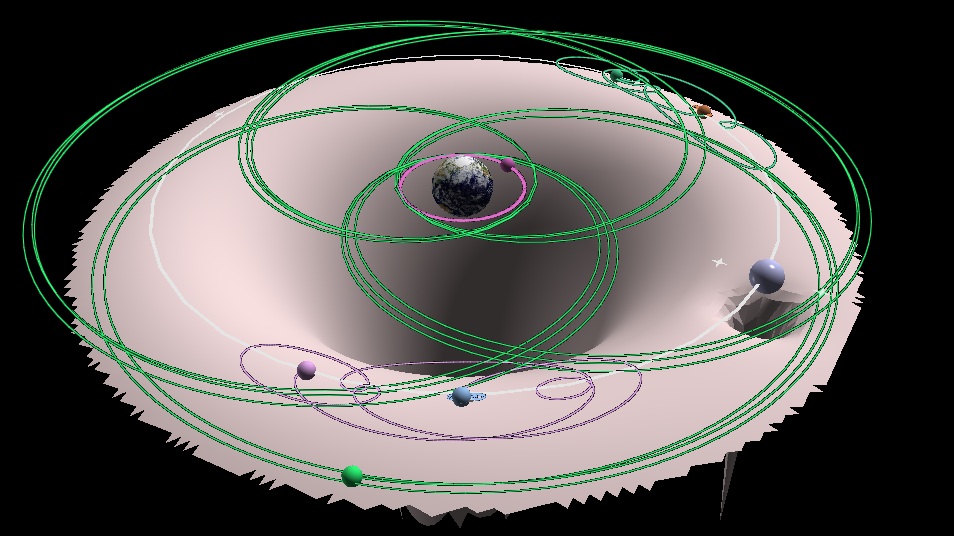
I also made a few side programs that aren't yet integrated into the main program to test some concepts. One just made a number of stationary objects in slightly different locations to experiment with generating random initial conditions for many objects. The other experimented with generating a surface to show the potential function for the system being simulated.
Next I need to work on implementing a way for the user to control the program while it runs, and working on developing scenarios for the program to run to illustrate Lagrange points, as well as working on my seminar.
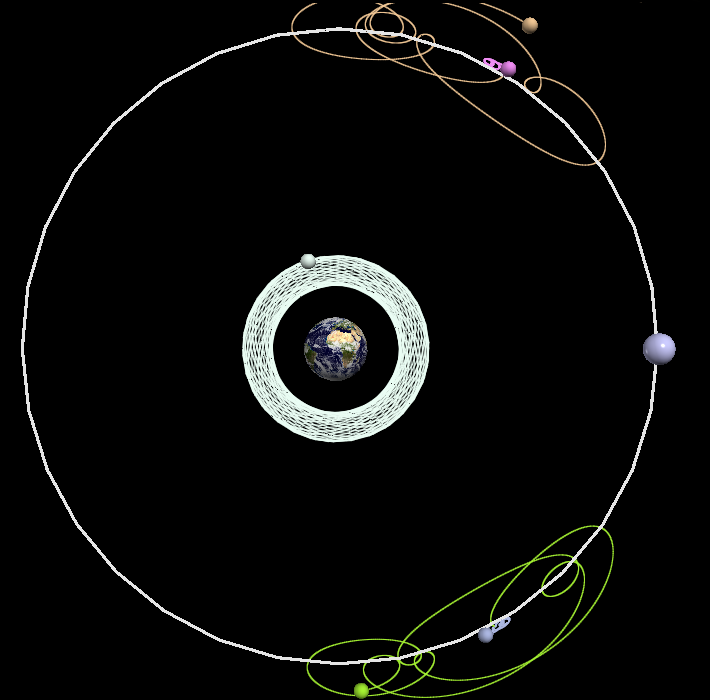
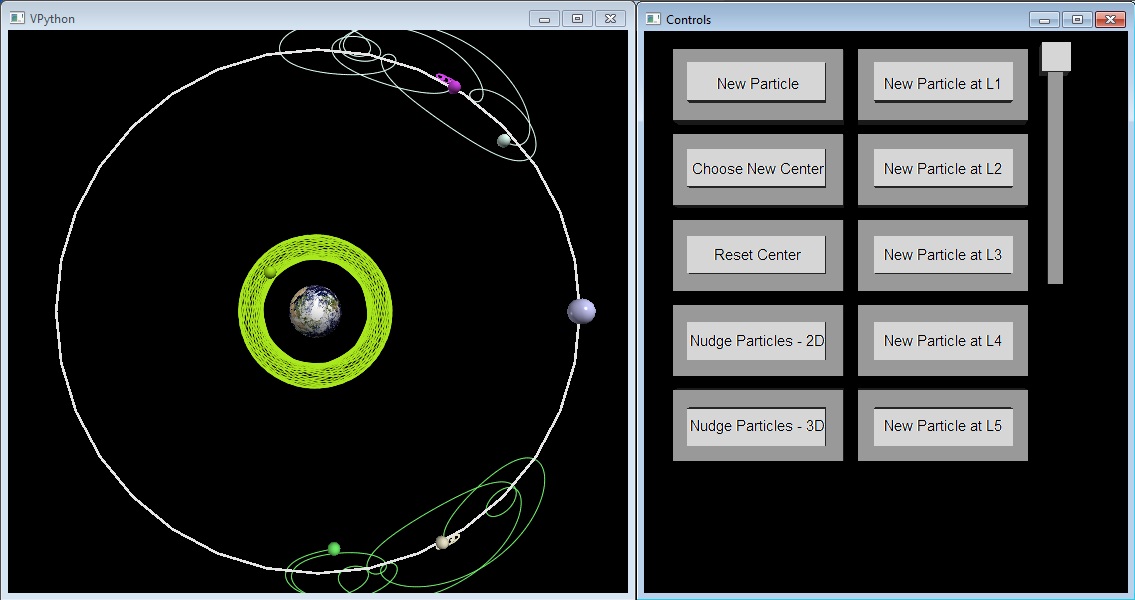
Update Wk12 11/10: New version of the VPython simulation, which has an equation solver to find the location of the L1-L3 Lagrange points. Implemented a control panel with buttons to change the location of the center of the scene and added a button to create a new particle with a user-determined position and velocity input via clicking. It sometimes requires a bit of clicking, but otherwise it seems to work pretty well. I attempted to implement a reset button, but it did not work, even with a couple different implementations. I decided to postpone that particular command until further notice, as it was not important and I can find more important uses of my time implementing other features.
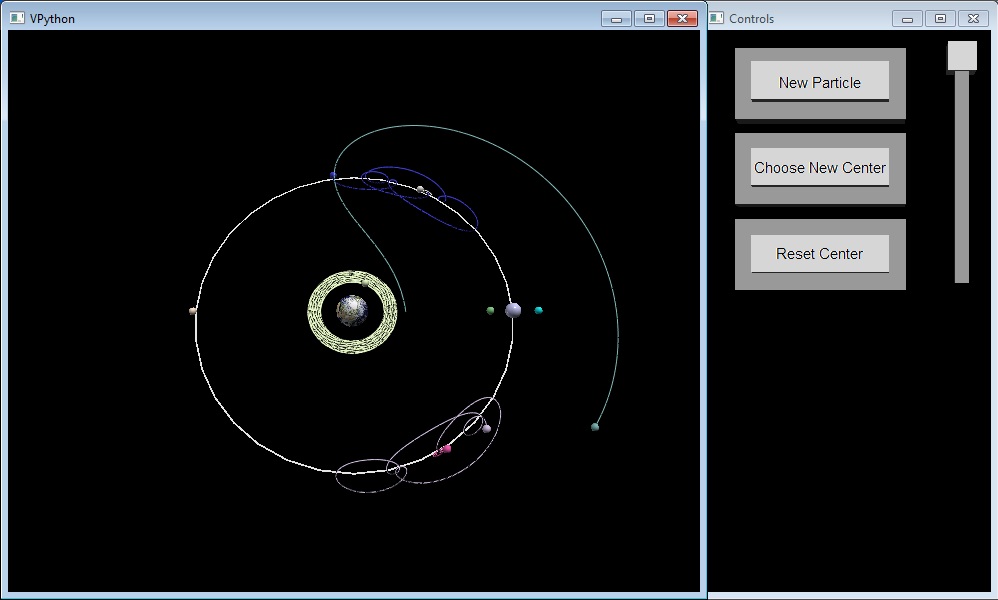
Update Wk12 11/12: The equation solver had to be re-implemented using Newtons method, as it was originally a function from a library not available on the default VPython install on lab computers, but that is fixed now. Added more user controls for the creation of particles at Lagrange points, and gave the user the ability to give the particles a small change in velocity so they can experiment with the stability of the system themselves. The animation now has a good working demo that people can experiment with, and it has controls for manipulating the system while the program is running, as long as VPython is installed.
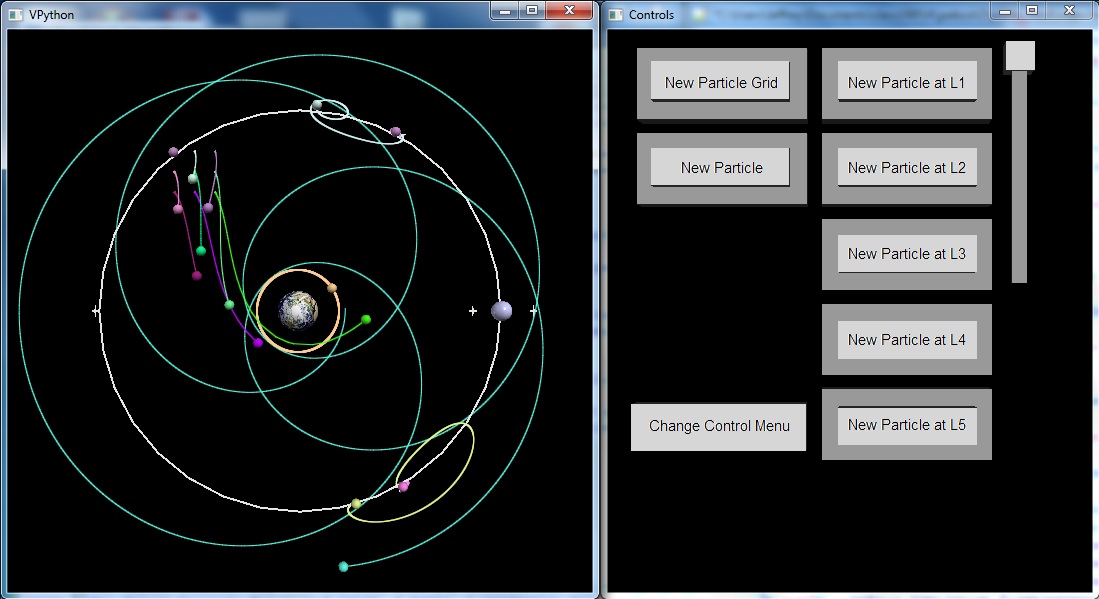
Update Wk14 12/04:
The control scheme of the program was greatly changed, with a few different control menus that can be changed using a drop down menu. This enables more functionality to be included without cluttering up the interface. In order to get the improved control panel working, a modified version of the button class had to be included that enabled the buttons to be turned invisible. Some new functions were added as well, and some functionality from one of the earlier side programs reintegrated into the main program and improved. Most of the features of the final RTICA should be implemented in this version
Return to Index.
Downloads:
RTICAs: All RTICA downloads require VPython to be installed to function.
Version 1: Circ. Restricted 3 Body Simulation
Version 2: Adds Runge-Kutta Integration
Version 3: Adds controls for particle creation
Demo Version 1: Adds more controls
Demo Version 2: Adds even more controls, refines control interface.
Demo Version 3: Reintegrated some features from branches and tweaked the code somewhat, most features should be implemented already.
Documentation:
Pre-Proposal
Original Proposal
Edited Proposal with First Update
Return to Index.
Return to Index.
Interesting Pictures:
Inclined Orbit

Jellyfish
Possible Orbital Resonance
Return to Index.
Index:
Abstract
About Lagrange Points
Progress Reports
Downloads
Interesting Pictures
References








