\begin{document}
\maketitle
 Last edited 17dec13 by Sean Cashin
cashin2@illinois.edu
Last edited 17dec13 by Sean Cashin
cashin2@illinois.edu
Find this document at http://new.math.uiuc.edu/math198/Math 198 Hypergraphics, Fall 2013
Here is an example of what I sought to create.
 .
.
no work is done on the particle and the kinetic energy remains constant.
 .
\section{How It Works}
.
\section{How It Works}
After the program opens, move the viewing window to access the command window.
Click anywhere on the viewing window to select an initial position for the test charge.
Enter desired mass, charge, and initial velocity vector components within the selected range.
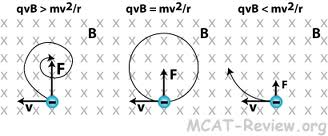
Note that the particle's speed does not change, but the centripital force of the magnetic field gets weaker as the z coordinate of the test charge's position increases.
\section{The Mathematics}
The force felt by a test charge moving through a magnetic field $B$ is
the cross product of the particle's velocity $V$ and the field vector
$B(x,y,z)$.
$F_b = qV \times B $
where $V=[v_x,v_y,v_z]$ is the velocity of the test particle with charge
$q$, located $(x,y,z)$ and $B=[b_x,b_y,b_z]$ is the magnetic field.
The contingent acceleration is a function of this force and the
particle's mass $m$.
$ a=\frac{F_b/ m} $
As the distance from the source of the magnetic field increases, the strength of the field decreases.
$F_b= (permiability constant*charge)/radius$ \section{The Process} I entered Math 198 with no previous computer programming background. The idea to create this program came from both a previous student's project about the conservation of momentum, and a program I used in high school physics about the motion of a test charge in an electric field called 'electric field hockey'. I learned how to use Visual Python from the bouncing ball, dipole, and cross product sample programs. I tried for hours to try to make a drag vector be the user input initial velocity, but after isolating a drag vector from the cross product sample program and setting the axis as an initial velocity, I realized the that program would not allow a changing input. I then decided that a time varying magnetic field would be very difficult for the user (and me) to comprehend, and not useful to explain with a program. I then decided to make the magnetic field constant with respect to time and varying with respect to position, since the force of a magnetic field depends on the distance to the magnet. For simplicity, I made the magnet face the observer and constant with respect to z. I ran into the odd problem of the test charge speeding up due to normal acceleration. Since a magnetic field does no work on a particle, this was a flaw. It disappeared however when the magnetic field begins to decrease, probably simply because it is sufficiently counteracted. For a complete description, see this narrative written in LaTex. \section{The Code}
 Last edited 17dec13 by Sean Cashin
cashin2@illinois.edu
Last edited 17dec13 by Sean Cashin
cashin2@illinois.eduFind this document at http://new.math.uiuc.edu/math198/
A Test Charge in a Variable Magnetic Field
by Sean Cashin
Math 198 Hypergraphics, Fall 2013
Abstract
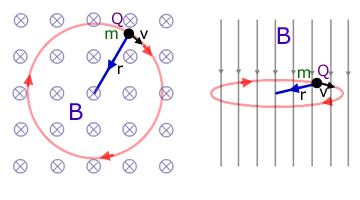
This program represents the magnitude of a magnetic field by demonstrating its effect on a test charge that is moving away from the source.
The force on the test charge is normal to both the test charge's velocity and the direction of the magnetic field.
The test charge's acceleration is a determined by the input mass, charge, and velocity, and most importantly the magnetic field's strength, which decreases as distance from the z=0 plane increases.
Here is a link to my proposal.
 .
.
 .
\section{How It Works}
.
\section{How It Works}
$F_b= (permiability constant*charge)/radius$ \section{The Process} I entered Math 198 with no previous computer programming background. The idea to create this program came from both a previous student's project about the conservation of momentum, and a program I used in high school physics about the motion of a test charge in an electric field called 'electric field hockey'. I learned how to use Visual Python from the bouncing ball, dipole, and cross product sample programs. I tried for hours to try to make a drag vector be the user input initial velocity, but after isolating a drag vector from the cross product sample program and setting the axis as an initial velocity, I realized the that program would not allow a changing input. I then decided that a time varying magnetic field would be very difficult for the user (and me) to comprehend, and not useful to explain with a program. I then decided to make the magnetic field constant with respect to time and varying with respect to position, since the force of a magnetic field depends on the distance to the magnet. For simplicity, I made the magnet face the observer and constant with respect to z. I ran into the odd problem of the test charge speeding up due to normal acceleration. Since a magnetic field does no work on a particle, this was a flaw. It disappeared however when the magnetic field begins to decrease, probably simply because it is sufficiently counteracted. For a complete description, see this narrative written in LaTex. \section{The Code}
#Project: Varying Magnetic Field by Sean Cashin, MA198, 2013
from visual import *
from math import*
print("""
Click to place a test charge with the input velocity, mass, and charge.
Try to get through the loops.
""")
scene.title="test charge in a magnetic field"
scene.width = 1000
scene.height = 1000
scene.autoscale = 0
scene.range = (60, 40, 10)
#Goals
plane=curve(pos=[(-40,-10,0),(-40,10,0),(-20,10,0),(-20,-10,0),(-40,-10,0)])
plane=curve(pos=[(40,10,10),(40,10,-10),(40,-10,-10),(40,-10,10),(40,10,10)])
#Test Charge Initial Conditions
tg= sphere(pos=(scene.mouse.getclick().pos), color=color.red, radius=1, make_trail=True )#testcharge
#tg.velocity=vector(1,0,0)
#tg.charge= 1
#tg.mass=1
#Magnetic Field
f=vector(0,0,10)
dt=.01 #increment
t=1
pi=math.pi
#User input
tg.mass=input('Test Charge Mass? Try 1-10: ')
tg.charge=input('Test Charge? Try 1-5: ')
tg.velocity=vector(input('Initial x Velocity? Try 1-5: '),input ('Initial y velocity?: '),input ('Initial z velocity? :'))
while True:
rate(100)
tg.pos=tg.pos+tg.velocity*dt
tg.velocity= tg.velocity+ dt*(cross(f,tg.velocity)*tg.charge)/(tg.mass)
t+= dt #increases t incrementally by dt
f=vector(0,0,(10/(1+tg.z)))
#f=vector(0,0, 10*cos(2*pi*t))#variable magnetic field
#if tg.x== 40: and tg.y<10 and tg.y>-10 and tg.z<10 and tg.z>-10:
#tg.velocity=0
#print "goal!"
- Here is a link to my program.
\end{document}