To simplify the incomprehensible complexity of Fluid Dyanimcs into a simple, cellular simulation governed by very simple rules based off real world observations
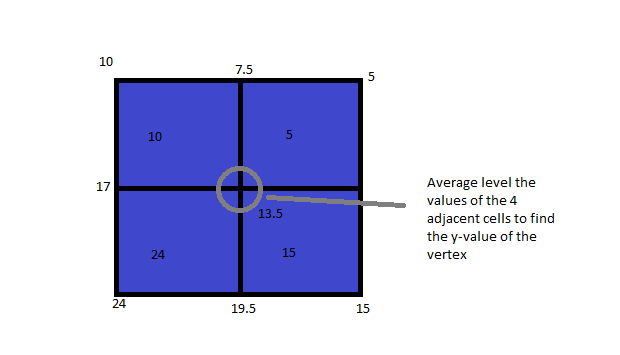
Graphics:The graphics for this program will consist of rectangle oriented in the X-Z Plane. The Y value of the rectangles will represent the the fluid level of the cells. The vertices for the rectangles are calculated calculated by averaging the level of the cells they define creating a smooth curve as illustrated in the diagrams below.
Rules: The fluid cells are based off 2 rules derived from real world observation
Rule 1: Adjacent cells tend to equalize their levels over time
Rule 2: Cells have momentum, a change in a cell tends to continue.

Math: The math of the simulation is based of the wave equation, which states that the acceleration of a wave is proportional to the 2nd degree gradient of position.

It is best to think of the wave equation model as imagining the water cells as balls attached to their neighbors by springs. If its neighbors are at the same level than the system will stay in equilibrium. If not the springs pull the neighboring cells towards each other. Since the balls have momentum, the system will osicillate.
From the wave equation and this understanding of the model simple, discreet equations can be made. On the discreet level, the Laplatian operator simply becomes an average of the levels of the cell's neighbors compared to its own. This yeilds the force on the cell which creates an acceleration. Assuming all the cells have the same mass, we say that this value gets added to the cells momentum in accordance to a small constant that accounts for unit conversions and the small time step dt.
The second equation is very simple. Basically the change in a cell's level is determined by its momentum.
