Last edited 14dec2011 by Alexander Paul
Alexander Paul / Math 198 / Fall 2011
Fractal patterns can occur in any n-dimensional space, but for an n-dimensional fractal, what (n-1)-dimensional patterns exist as a slice of the orginial. My project aims to visualize these fractals-within-a-fractal by first generating a 3-dimensioal fractal, then applying a plane through it. By only showing points on the fractal that lie on or very near the given plane, a 2-dimensional pattern should emerge. In this project, I examine 4 dimensional Julia sets and the 4 dimensional mandelbrot set, using two programs that generate 3 and 2-dimensional sets, respectively.
In order to understand how these fractals work in the first place, we first have to understand complex numbers. Complex numbers have a real component and an imaginary component, and are represented as:
where:
the magnitude of a complex number is:
and its square is:
The Mandelbrot set is the set of complex numbers such that for any complex number, 'c', in the set, the following iterative formula stays bounded (does not go towards infinity as number of iterations goes to infinity):
The Julia set is closely related to the Mandelbrot set. The iterative formula is exactly the same, except, unlike in the Mandelbrot set, where the complex point in the set was 'c', this time the point is the intial value of 'z', and the 'c' remains constant for all points in a particular Julia set.
So to create 2-dimensional fractals, we only needed to use regular complex numbers. With one real and one imaginary component, that gave us 2 axes to plot points on. Making 3-dimensional fractals is harder, because it turns out that there is no 3-term set of complex numbers that behaves in the proper way to give us the proper results for our formulas. Solution? Quaternions. Quaternions are a 4-term set of complex numbers with one real and three imaginary components. A quaternionic number is written in the form:
By replacing the complex numbers in the Julia formula with quaternionic numbers, we can create a 4-dimensional fractal. Unfortunately, there was a problem with this idea: multiplying quaternions is not the same as multiplying ordinary complex numbers. For example, the commutative property does not hold for quaternions:
but
Conveniently, however, when a quaternion is multiplied by itself, as it is in our formula, the expression for multiplication can be simplified to: 2
But, since we want to graph a 3-dimensional set, we hold one of the dimensions of the quaternion constant, thus allowing us to create an array of 3D Julia sets that describe, as a whole, a 4D Julia set.
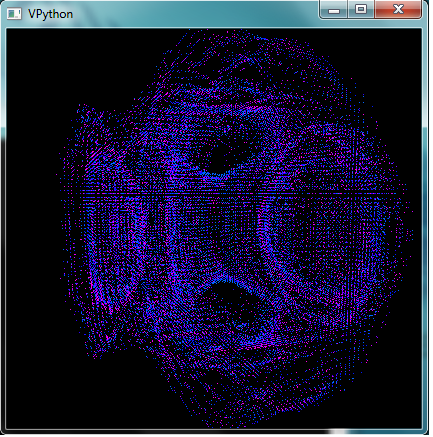
Now, what I was interested in examining was whether or not the 2D Julia and Mandelbrot fractals still existed inside their 3D counterparts. By holding a second variable constant, I was able to constrict the resulting shape to just two dimensions, and lo and behold, many different 2D Julia fractals became visible as a shifted through different planes in 3D space.
Operation instructions for running my two progams and how to manipulate them to draw you different Julia and Mandelbrot sets can be found here.
Follow these links for the 3-Dimensional and 2-Dimensional Python progam code.