Math198 - Hypergraphics
Last Modified recently

3D Life


Contents

Abstract
Brief Overview
Introduction to the Game of Life
3D Life





Abstract

The goal of this project is to create a 3 dimensional cellular automaton that would follow rules similar to Conway's Game of Life, except with the addition of a neighbor in both the near and far directions, and then look for any patterns that may emerge.

Back to Top

Brief Overview

Back to Top

Introduction on the Game of Life

Conway's Game of life is a 2 dimensional cellular automaton that evolves into many interesting configurations based on certain initial conditions. The Game of Life consists of a grid of cells each of which is in one of 2 states: dead or alive. Each cell also belongs to a neighborhood. There are many ways to define a neighborhood, in the Game of Life however the neighborhood is defined to be the 8 cells adjacent to the cell in question. The state of each cell in the next generation is determined by the state of its neighborhood, these are the rules for the automaton. In the Game of Life the rules are: A dead cell with exactly 3 live neighbors becomes alive, a live cell with either 2 or 3 live neighbors continues to be alive, and in all other cases the cell is dead in the next generation. The rules of a cellular automaton are applied to every cell simultaneously.

Most initial starting conditions in the game of life will stabilize over time. There are three kinds of stabilizations that have been identified, they are still lives, oscillators, and spaceships. Still lives reach a certain state and then no longer change from generation to generation. Oscillators will oscillate between certain states as the generations go on. Spaceships are patterns that oscillate between certain states but will also fly off in a certain direction indefinitely. Examples of each type of stable state are shown below. (Pictures courtesy of http://en.wikipedia.org/wiki/Conway's_Game_of_Life)

A still life that is called a "boat"

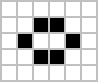
A still life called a "beehive"

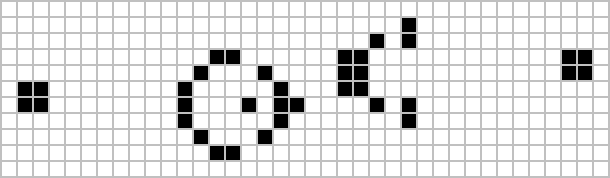
An oscillators called a "pulsar"

A spaceship called a "glider"

However the more interesting patterns are the ones that grow indefinately. The first example of a pattern like this is Gosper's glider gun, which will produce a glider every thirty generations.

The gun in it's initail position.

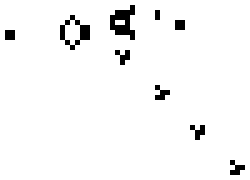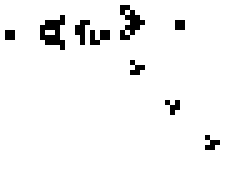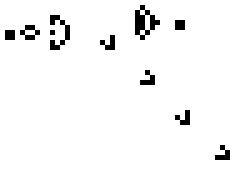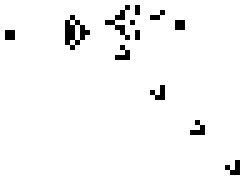
The glider gun in action.



However there exist patterns that exhibit even more interesting behaviors such as universal constructors and patterns that simulate the activities of a computer. Where a universal contructor is a patteren that can create copies of itself (example below).

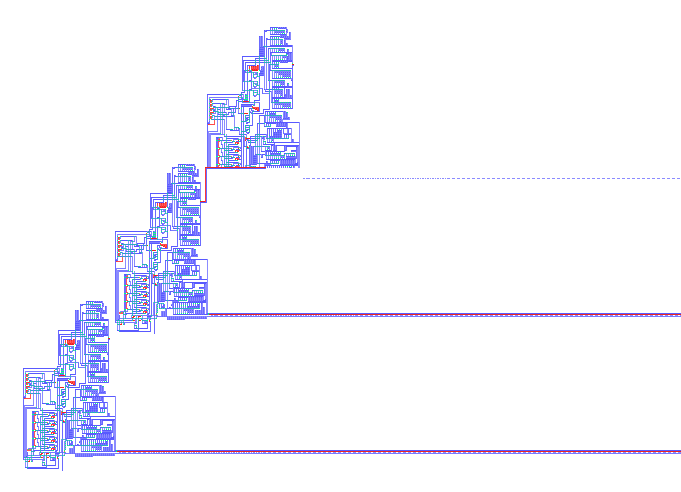
Each one of the stuctures in the above picture creates a new, identical structure above itself



Back to Top

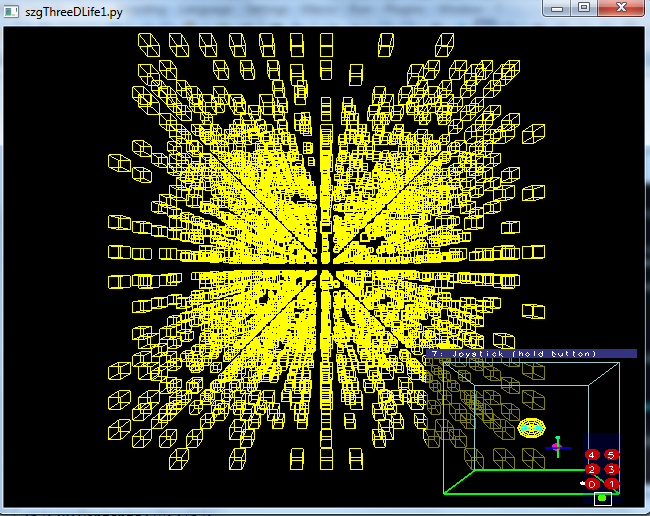
3D Life program.

3D life

The program I created, draws a 3 dimensional lattice that updates according to the rules of the game of life, that is that any a live cell with either 2 or 3 live neighbors will be alive in the next generation, and a dead cell that has 3 live neighbors will be alive in the next generation, all other cells will be dead in the next generation. The only difference between my program and the traditional 2D game of life is that I have added 2 neighbors on the near-far axis to the traditional 8 neighbors in the 2D Game of Life.



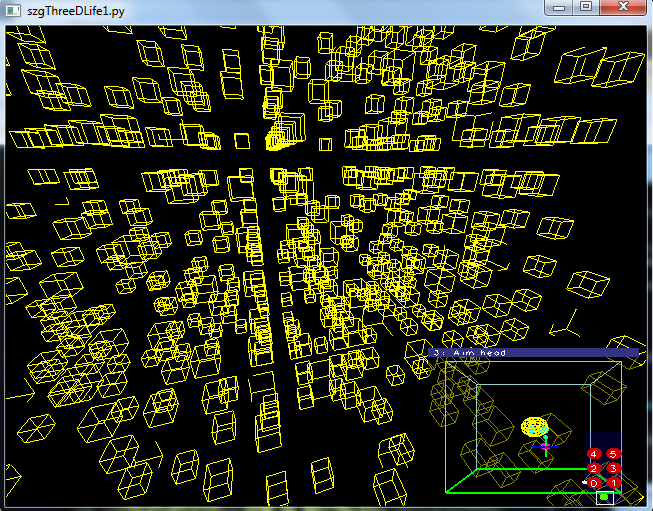
In contrast to the 2 dimensional Game of Life, the stuctures of a 3D Game tend to remain chaotic even a few thouseand generations in. This does not necessarily mean that the sturctures of the 3D Game are chaotic however. Since the addition of another dimension adds a huge amount of possible combinations of live and dead neighbors a cell could have. Some other possible explainations for the lack of any emerging pattern are that either a pattern in a 3D Game takes much longer to emerge than in 2 dimensions, or that there is a ocilating structure that emerges with a very large period of ociallation making it difficult to detect. At first the program I wrote generated a initial state for the automaton randomly each time the program was run. The problem with this was that the first generation could neither be recorded or reproduced easily. Later this problem was solved by using a second program that would generate a list that could be copied and pasted into the program in lieu of a random starting configuration.