Last edited 3dec10 by moss3@illinois.edu
HyperLatin2: Generating a Four-Dimensional Latin Square
Abstract
The goal of my project was to create a brute-force algorithm for generating a four-dimensional Latin Square and create a computer interface that demonstrates it. The project was written in C and uses OpenGL. The program compiles using MVC98 after running vcvars32.bat and using the run command, assuming run.bat and win.mf are in the same folder as the source file.
The Game
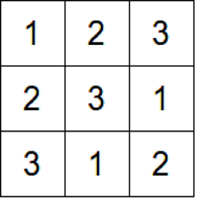
A Latin square is basically a square grid in which each of the spaces on the grid is entered a number between one and the maximum number of spaces in that row or column. For example, if the square has five spaces per side, each row and column must contain the numbers one through five. Research in Latin Squares has led to advances in combinatorics and experimental design. Also, the coming of Sudoku has made solving Latin Squares a very popular recreational activity, as all solved Sudoku are 9x9 Latin Squares. My project creates a variation of this puzzle, except the grid is four-dimensional and it is played using a three-dimensional computer interface.
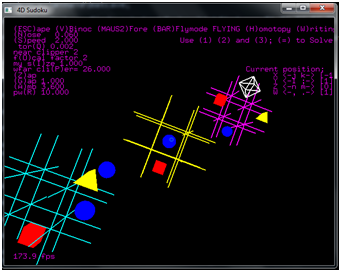
First, it is counterintuitive to fill a three-dimensional space with the two-dimensional symbols that we use for numbers. Thus my program uses a blue sphere, a red cube, and the yellow tetrahedron instead of the numbers 1, 2, and 3. Also, instead of a single 9x9 grid, this puzzle consists of three3x3x3 grids. In addition to rows and columns, the grids also have a depth axis, which has three spaces that must each contain all three symbols. Also, each grids represents a projection of a full hypercube (four-dimensional cube); the corners of each of the three cubes are considered to be on the fourth axis. These are the four dimensions of my Sudoku puzzle. True to the original Sudoku, this puzzle also has 81 spaces.

Each row along the four axes must contain a sphere, a cube, and a tetrahedron. In this picture the near-upper-left corners of each grid are considered to be in the same row.
Setting Up a Puzzle
My program contains an option for users to set up a puzzle for the solving algorithm to solve. Pressing the "c" key will disable most of the keyboard inputs used to control camera motion (the camera can still be controlled using the mouse and mouse buttons) and cause a white cursor to appear in the grids. This cursor can be moved to other spaces using the "a", "d", "e", "s", "i", "k", "j", and "l" keys. By selecting a space with the cursor and pressing the 1, 2, and 3 keys, the user can place spheres, cubes, and tetrahedrons in the puzzle gird. The algorithm will consider these spaces to be initial values, and will try to find a solution that incorporates these given spaces.
The Solving Algorithm
My brute force solving algorithm solves the puzzle one space at a time. It was inspird by a "brute-force" algorithm that is sometimes used to solve Sudoku puzzles. Pressing the "=" key solves a single space.
My brute force solving algorithm takes the following steps:
1) Start at an initial position.
2) Check if the space has an initial value (i.e. a value entered by the user to test the algorithm).
-If it does and the solver is proceeding, skip over the space and proceed to the next space in the sequence. Skip Steps 3-7.
-If it does and the solver is backtracking, proceed to a previous space without erasing the symbol initially entered. Skip Steps 3-7.
-If no initial value is present, proceed to step 3.
3)If the space is empty, check each row along the four axes for a sphere.
- if a sphere is not found, enter a sphere into the space and continue to the next space. Skip Steps 4-6. The solver is now proceeding.
-if a sphere is found or the space is empty, go to step 3.
4)If the space is still empty or the algorithm previously entered a sphere , check each row along the four axes for a cube.
- if a cube is not found, enter a cube into the space and continue to the next space. Skip Steps 5-6. The solver is now proceeding.
-if a sphere is found, go to step 5.
5)If the space is still empty or the algorithm previously entered a cube , check each row along the four axes for a tetrahedron.
- if a tetrahedron is not found, enter a tetrahedron into the space and continue to the next space. Skip Step 6. The solver is now proceeding.
-if a tetrahedron is found, go to step 6.
6)None of the three symbols are viable options for that space; erase the previous value of that space and move to the previous space. The solver is now backtracking.
7)If the solver has backtracked past the initial position, declare the puzzle impossible and terminate the program. See note below.
8) Repeat Steps 2-7 until the last space is filled (i.e. the puzzle is solved).
Note on Step 7: If the puzzle must backtrack past the initial position, then it has reached a point in the puzzle where it has tried all possible permutations of symbols and none would create a viable solution. Therefore, the puzzle is impossible.
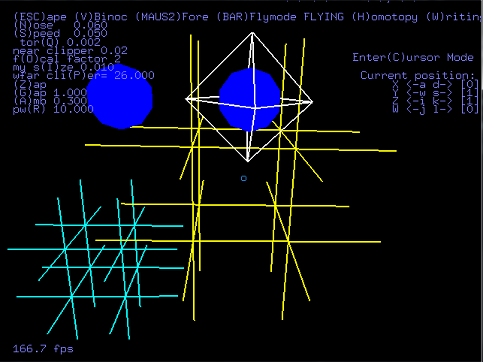
An impossible puzzle. Because these two spheres were entered by the user, the solving algorithm will attempt to find a solution that incorporates these two spheres. But since there is no longer room in that row for both a cube and a tetrahedron, the row cannot be solved. The solver will try many permutations of symbols before declaring the puzzle inpossible.
It should be noted that a brute-force algorithm only finds one solution to a puzzle, even though a given puzzle may have many solutions. For example, if the algorithm is run to completion on a blank game grid, it will return the same solution every time despite the fact that there are many other possible ways to make a four-dimensional Sudoku solution. Also, the algorithm does not account for a changing puzzle; if the user enters symbols after the algorithm has begun solving, the algorithm may declare that an invalid solution is valid.
Improvements:
Some improvements to the program would include:
-an algorithm that generates random puzzles for the user (or the solving algorithm) to solve
-a more efficient method of drawing the grids
-having it run in a more modern compiler
Interesting and Relevant Links
A brief history of Latin squares
A detailed description of the brute-force Sudoku algorithm that inspired the project
A more advanced Sudoku solver