
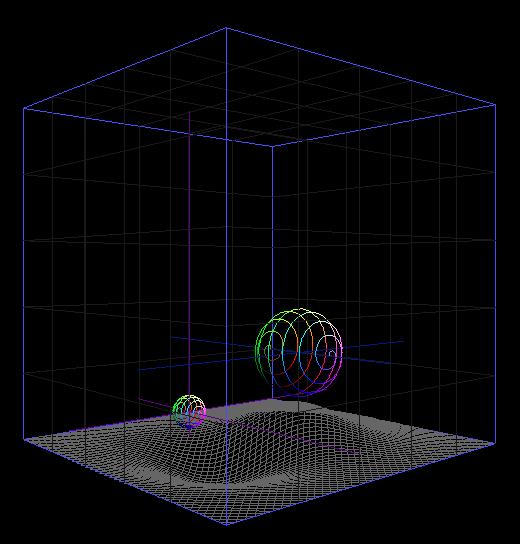


The math involved is rather simple since the movement of the spheres is essentially projectile motion with collisions. The kinematic equation xf=xi+vt+at2/2 is the basis which was demonstrated by Curtis Woodruff's first prototype program but was tragically lost to overwriting.
Collision was slightly more difficult. Bouncing of the walls was merely detecting when a bounce would occur and then switching the appropriate velocity. Only one would be needed to be switched since the walls were flat at first and the object was a sphere. When simulating ball-ball collisions, the math became a bit more difficult, but with the help of Thayer Watkins' page on elastic collisions, we were able to get the proper equations for the path of the spheres.
It was important that spheres were used since the unit vector when two balls collide is the same as the line between the center of the spheres. Conservation of momentum holds true for all collisions, and conservation of energy holds true for elastic collisions. While we later changed this, we assumed these two to be true for the following equations.

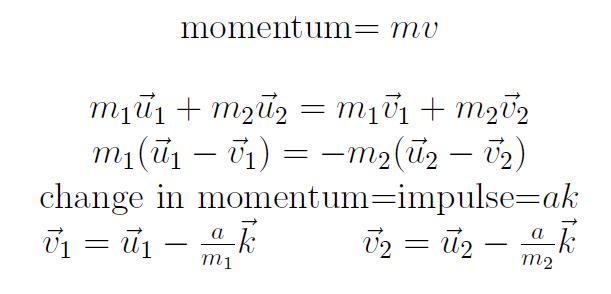
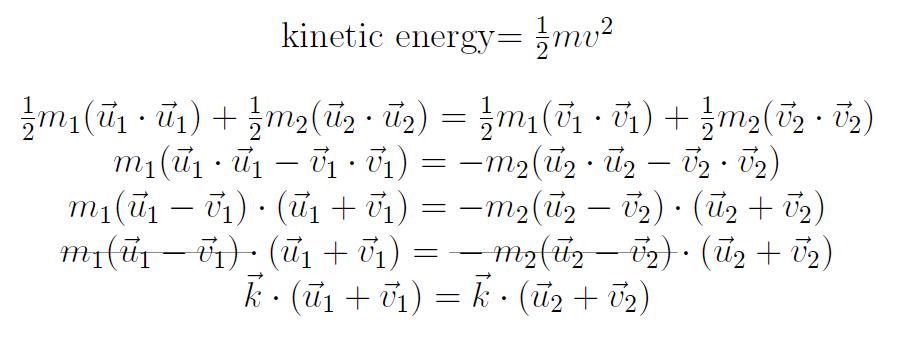
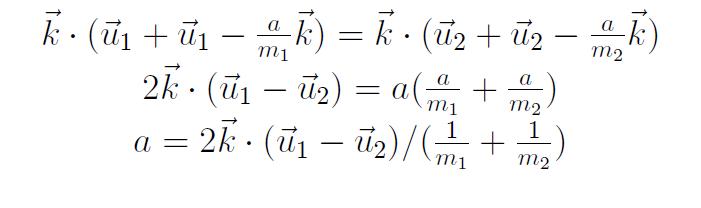
The definition of the "a" constant was a mystery to Curtis and me. While I had assumed it was impulse since it was related to the change in momentum, Professor Francis seemed to think otherwise. As a note for the future, it would be best to find out what it represents.
Using ![]() , both the ball-ball and ball-curved ground collisions were solved. The ground simply was represented as a plane of tiny spheres with infinite mass. Actually, to say that "solved" the collisions would be horribly exaggerating. The detection method for both were rather shoddy and still are. Multiple simultaneous collisions as well holes in the tests were quite evident, but Curtis and I eventually settled on a final method that gave optimal results. This method surprisingly came from working on the loxodromic spheres that Professor Francis suggested. Rather than sweeping points on the plane to test the distance from the center of the sphere to, we used the same spiral pattern used by the sphere to create a distribution from the verticle line passing through the center of the sphere. This can actually be seen as a spiral set of points on the ground shadowing the balls as they move in our final program.
, both the ball-ball and ball-curved ground collisions were solved. The ground simply was represented as a plane of tiny spheres with infinite mass. Actually, to say that "solved" the collisions would be horribly exaggerating. The detection method for both were rather shoddy and still are. Multiple simultaneous collisions as well holes in the tests were quite evident, but Curtis and I eventually settled on a final method that gave optimal results. This method surprisingly came from working on the loxodromic spheres that Professor Francis suggested. Rather than sweeping points on the plane to test the distance from the center of the sphere to, we used the same spiral pattern used by the sphere to create a distribution from the verticle line passing through the center of the sphere. This can actually be seen as a spiral set of points on the ground shadowing the balls as they move in our final program.
We had intended for this to be used in the CUBE, but due to scheduling conflicts and other setbacks, the date for demonstration may be delayed. However, after working in aszgard and modifying it for compatibility, we believe we have a functional program affectionately named ballball.cpp.
The program still has many bugs that can be addressed, but the next step would be to add sound and a moving ground plane. Sound is out of my realm of knowledge, we actually did manage to have the plane move while playing around with possibilities. It crashed so many times that it was about as practicle as my "disco" floor that incorporated changing lights on the ground plane. Adding sound to this would of course beg making a dance club, which I would suppose future students may try. Really, the ball-in-a-box can be used as a platform to be expanded upon. The fact that it almost simulates sliding as well opens up a large range of possibilities. Perhaps, a 3D pinball machine would be possible.
Related materials can be found in the public file.