Last edited 17dec09 by rosboro1

Calabi-Yau shapes

Ben Rosborough

For my semester project, I am going to be modeling what are known as a Calabi-Yau shapes. These shapes, or manifolds, appear in what physicists call string theory. This theory is motivated by two other conflicting theories of our Universe- quantum mechanics and general relativity. String theory proposes that our Universe contains not only the three spatial dimensions that we are accustomed to, but also six additional spatial dimensions. These extra dimensions are extremely tiny, curled up into shapes known as Calabi-Yau shapes.

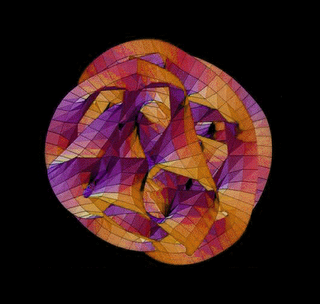
This is an example of a Calabi-Yau shape.

There are many different shapes that are considered to be Calabi-Yau shapes, this is just one of many.

This project consists of a few different parts:

1) Obtain a sufficient understanding of Calabi-Yau shapes, and methods of visualizing extra dimensions.

2) Work with various examples of Calabi-Yau shapes found online to first understand the code used to visualize the shape, and then to create an original Calabi-Yau shape.

3)Using Mathematica, insert project into the Cube.

I am currently slogging through some Mathematica code to understand how the shape was put together.

Final Update

I was able to isolate the exact equations that were used to display the Calabi-Yau shape, and understand how it was put together. The Calabi-Yau shape is defined in six spatial dimensions. It is of the form x₁ⁿ + x₂ⁿ + x₃ⁿ + x₄ⁿ + x₅ⁿ = 0. One can then set a pair of variables to be constant. This allows to show a 4 dimensional slice of the actual 6 dimenisonal shape. This 4-D slice is projected into 3-D where we can view it in Mathematica.

The shape is made using the complex definitions of the sine and cosine functions: Sin(x)=(e^ix - e^-ix)2i, and Cos(x)=(e^ix + e^-ix)/2. These equations can both be multiplied by a phase factor that shifts them, depending on the value of a certain variable.

These equations are utilized in a parametric plot. The X component is the the Real part of the sine multiplied by a phase factor. The Y component is the Real part of the cosine multipled by a phase factor. Finally, the Z component is the Imaginary part of the sine multiplied by the cosine of an angle alpha, plus the Imaginary part of the cosine multiplied by the sine of an angle alpha. This angle alpha is the projection angle in 3-D.

Mathematica uses these equations to graph 25 separate parametric plots. They each represent a set of two values for two different variables in the X,Y, and Z components. Showing all of the plots on one graph represents the final, 3D projection of a 6D shape.

I have two Mathematica notebooks to show. The first one animates the shape through different projection angles. This angle is between 0 and 2pi. The tools of Mathematica allow one to slow down the animation and get a really good sense of how the shape is changing. The other notebook is an animation of a grid of Calabi-Yau shapes. This is what I really wanted to show, because it is a good visualization of how tiny extra dimensions in our universe may actually exist.