Math198 - Hypergraphics
Last Modified 12/12/09 by Andrew Lee
VPython Robotic Arm

Quick Links
Abstract
The goal of this project was to create an interactive animation of
a robotic arm in VPython that consists of a triple jointed arm that rotates
about a central axis and responds to user inputs. The movement and function
of this robotic arm is illustrated through its ability to pick up, move, and
set down an object.
Back to Top
Objectives
- Modify Bruce Sherwood's doublependulum.py example to look more like a robotic
arm and document how it works.(Click here
to see the original.)
- Explore the use of keyboard inputs to control an animation.
- Define a coordinate system on which the movement of the robotic arm can be
based (as opposed to controlling the arm by rotating the arm(s) by an angle.
- Add a third joint and section to the arm.
- Define a task for the robotic arm to complete.
- Find a way to automate the arm's functions.
Back to Top
Design

From what I have seen, the design I used for my robotic arm is a fairly common one.
It consists of three segments connected at three joints. Each of the three joints
allows of rotation about one axis. In addition, the entire arm can rotate about a
vertical central axis. This configuration seems to be versatile and gives the arm
a good range of motion.
When talking about robotic arms (and many mechanical systems in general), the term
"degrees of freedom" comes up often. In simple terms, "degrees of freedom" refers
to how many ways there are for something to move. In a traditional (cartesian)
3-dimensional coordinate system, there are a total of six degrees of freedom:
translational in the x, y, and z directions, and then rotational about the x, y,
and z axes. For example, the joint between the first and second segment of my
robotic arm has only one degree of freedom (zero translational, one rotational).
It is possible that this type of robotic arm is popular because it is very similar
to the human arm in function, consisting of an "upper arm," "lower arm," and some
sort of "hand." Of course, even having a similar overall layout, there are a number
of variations on this type of robotic arm, particularly when it comes to degrees of
freedom.
The human arm actually has a total of seven degrees of freedom (three rotational in
the shoulder, one rotational in the elbow, and another three rotational in the wrist).
My robotic arm has four degrees of freedom (two rotational in the "shoulder," one rotational
in the "elbow," and one rotational in the "wrist"). Obviously, robotic arms can have any
number of degrees of freedom depending on the function and complexity.
Originally, I wanted my robotic arm to be able to "draw" on a platform based on user inputs.
However, Professor Francis suggested that picking up and moving objects might be a more
interesting demonstration, so that is the route I ended up taking. In either case, my
robotic arm is based on Bruce Sherwood's doublependulum.py. In some sense, a pendulum is
a very simple robotic arm; by adding more sections and joints it becomes more functional
and complex.
For the sake of simplicity, my arm does not really have a hand (it cannot grip anything
or otherwise do anything with the last section of the arm). However, for the purposes of
my demo, it was not strictly necessary for the arm to be able to grip anything. Realistically,
we can think of my particular arm as having an electromagnet attached to the end of it so
that it can pick up and release an object without having any moving parts at the end.
Back to Top
How the Program Works
Frames
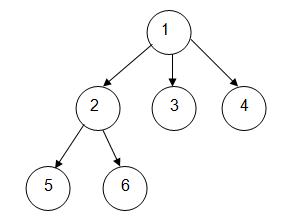
In creating this program, I had to learn much about what "frames" were and how to use them.
Simply put, "frames" are Python's way of setting up a hierarchy (scene graph, parent-child
relationships, tree structure, etc.). Like in many programs, the use of frames was very
important in creating my robotic arm; without them it would have been extremely difficult
if not impossible to do so.
In Python, the syntax of setting up a frame is a little strange, making them somewhat
difficult to understand at first. We can begin by setting up a central, main frame that
refers to the whole "world" within the program. Let's call this "frameworld."
frameworld = frame()
From there we can define another frame that is now dependent on "frameworld." Let's call
this "frame1."
frame1 = frame(frame=frameworld)
Already we can see that the syntax is odd with the word "frame" thrown around quite a bit.
However, it is fairly simple; what the above line is saying is "define the word 'frame1'
to be a frame whose parent frame is 'frameworld.'" By adding the following lines into the
program
frame2 = frame(frame=frame1)
frame3 = frame(frame=frame1)
frame4 = frame(frame=frame1)
frame5 = frame(frame=frame2)
frame6 = frame(frame=frame2)
We can set up a hierarchy that graphically looks like the picture above. Like other objects
in Python, frames have other attributes (such as position and axis) that can be defined as
desired.
What frames actually do in my program is allow parts to be physically linked to each other.
In other words, because the frames of each section of my robotic arm are dependent on the
section before it (by defining them as such in the program), by rotating the upper section
about the "shoulder," the rest of the arm rotates with it accordingly. Without frames, such
a rotation would simply result in the arm "breaking" at the elbow; that is, the upper arm
would rotate but the rest of the arm would remain stationary and the arm would no longer
be physically connected.
Frames can also serve as reference points. For instance, in my program, I set up a frame
a certain distance from the base of the arm. I then based objects such as the main platform,
the grid, etc. off of that frame, meaning that the frame served as a new "origin" point for
those objects.
Movement
To make the robotic arm move, I essentially wrote another "language" within my program. I
created commands like "u," "g1," and "cfa" which correspond to "move the arm vertically up,"
"move the arm to grid position #1," and "change the object's frame to the frame of the tip
of the arm" respectively. What actually happens when the user presses, for instance, the "3"
key is that the program responds by inputting a list of these commands into a main list (for
example, pressing "3" results in ["d", "cfa", "u", "g3", "d", "cfg3", "u"] being inserted
into another list). When the enter key is pressed, the program then reads this list and interprets
them as movements (move down to z=0, change object's frame to arm's frame, move up to z=0.2, etc.),
performs the necessary calculations, and moves accordingly.
While this seems like an overly complex way to set up the program, I did it this way because
it has the advantages of being able to use one set of commands in different configurations
(rather than setting up repetitive individual command lists) and also allows for easy
reconfiguration (you could theoretically edit the lists to make the arm do whatever you
wanted for a particular keystroke). The disadvantage, however, is that the commands are
limited (right now there are a total of about 23) so the arm is only capable of doing a
select number of things (hence it can only move the object to one of 10 locations vs.
being able to move it to any desired location on screen).
Back to Top
The Math Behind the Arm
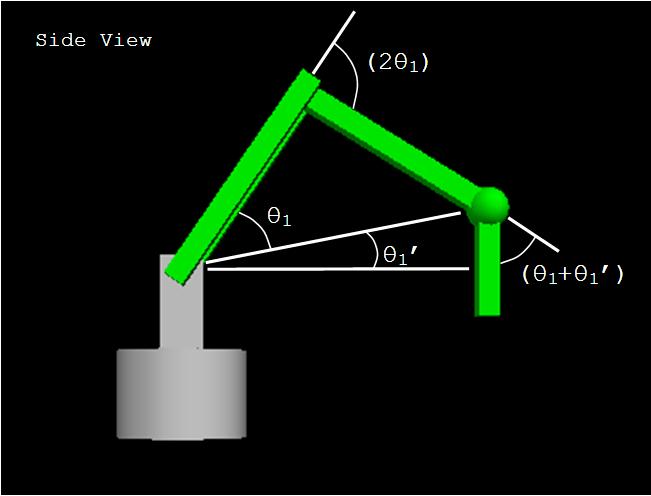
Geometry
With only four degrees of freedom, the geometry of my robotic arm is relatively simple.
There are basically four angles that the program controls (obviously one for each joint/axis).
To further simplify things, I linked some of the angles together so that they always move
together proportionally (for example, in the above picture, the "elbow" angle is always
twice that of the shoulder angle θ1, and the wrist angle is always equal to
θ1 + θ1'). So in reality, the only angles we need to
worry about are θ1, θ1', and α, and the rest will
be based on those three angles.
Of course, when using this program, the user does not control individual arm angles. As in
most robots, the arm is moved through some sort of a coordinate system, and the program
takes care of the actual angles behind the scenes. So you may be asking yourself, what
kind of coordinate system does this robot run on? Well, seeing how as though we're dealing
with angles, rotations, and distances, it's not surprising that the arm actually has a native
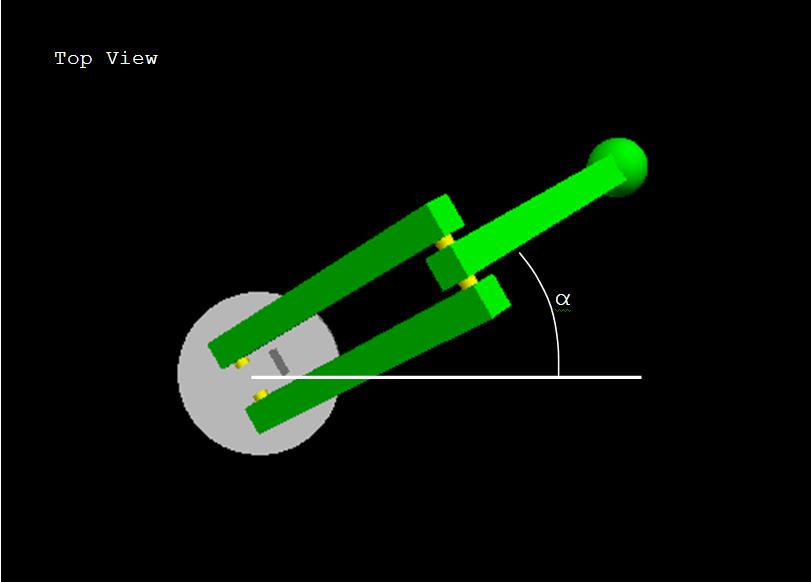
coordinate system similar to those of polar coordinates. Looking from the top, the base of
the arm serves as our "pole," and using angle α and the distance the arm reaches out
as our (r, θ), we get a something very similar to traditional polar coordinates. There
are some major differences, however, in that this arm also moves up and down in the z axis, and
that the "radius" is calculated in a rather complex manner.
For the purpose of keeping things simple, I said that the arm actually has two "radii," one
being the "actual" radius that runs straight from the shoulder joint to the wrist, and
the other being the "projected" radius which is just the component of the "actual" radius
parallel to the platform surface. In other words, the "projected" radius is the radius from
the "pole" to the tip of the "hand," and this is the radius we typically think of when we
think of polar coordinates.
Now when the arm is level (that is, θ1' = 0), the "actual" and "projected"
radii are equal to each other. It is only when the height of the "hand" changes and the
"actual" radius becomes tilted that things become interesting (it goes from polar coordinates
to something like a combination of cylindrical and spherical coordinates).
So what exactly goes on in the program when you press a key? Based on where you want the
arm to go, three things are specified: a target "z" value, a target "radius" (projected),
and a target angle α. Based on these three values, the program first calculates
the angle θ1' by taking tan-1(z / "projected" radius). It then calculates
what the "actual" radius needs to be by dividing the "projected" radius by cos(θ1').
After that, it calculates what θ1 should be by taking cos-1("actual radius"
/ (2 x length of the arm)).
Just as a little side note, I thought I'd mention rectangular coordinates. When I originally designed
my robotic arm, I thought I would have to create a rectangular coordinate system off which I could
base the coordinates of locations, etc. After actually creating my program, it turned out that
rectangular coordinates were not actually necessary. However, I thought it would be an interesting
idea to explore anyway. It turns out that because of the way I set up the program and the calculations,
converting the coordinates to a rectangular coordinate system was fairly easy. It was as simple as
plugging numbers into the familiar equations x=rcos(θ) and y=rsin(θ). Introducing a couple
of lines to the program allowed it to use target x, y, and z values instead.
(Click here to see my demo of rectangular coordinates.)
Anyways, back to the calculations.
Once the program does the above calculations, it has target θ1, θ1',
and α angles. The program also has the current θ1, θ1',
and α values saved. By taking the difference between the two it can find the angles by which
it must rotate to reach the target location. Once it does that, it rotates the arm first about the
"shoulder," then the "elbow," then the "wrist." It then rotates the arm about the shoulder about the
other axis (angle α), and finally, it rotates the arm about the shoulder again by angle
θ1'.
Of course, all of these rotations do not happen at once. If they did, the arm would look as if it
were instantaneously jumping from one location to another! Instead, the arm moves in small steps
until it reaches its target location using interpolation.
Linear vs. Sinusoidal Interpolation
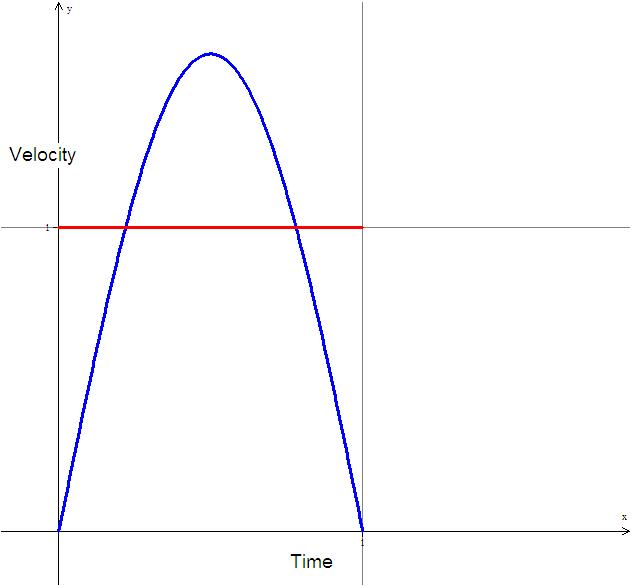
For a change in position over the course of one unit of time (t=0 to t=1), the equations
for linear and sinusoidal interpolation is as follows:
Linear
x(t) = xi(1-t) + xf(t)
Sinusoidal
x(t) = xi(cos2(π t / 2)) + xf(sin2(π t / 2))
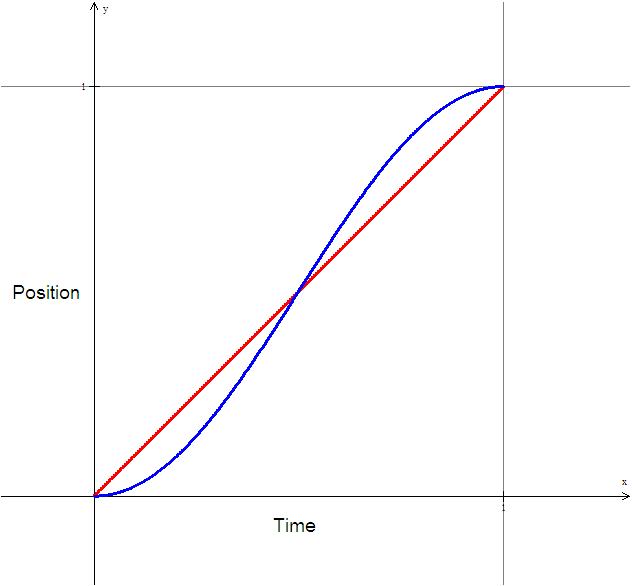
The graphs above show example position vs. time and velocity vs. time graphs for an object going
from x=0 to x=1 during the interval t=0 to t=1. Obviously they get to the same place in the same
amount of time, but the important thing is how they get there. Looking at the velocity graph, they
are very different. The linear interpolation has a constant velocity and the sinusoidal interpolation
has (not surprisingly) a sinusoidal velocity curve.
What this translates to in an animation is that for linear interpolation, the arm goes from a standstill
to a velocity of 1 instantaneously, moves at a constant speed, then stops instantaneously, whereas
for sinusoidal interpolation, the arm starts at a standstill, slowly accelerates, decelerates, and
finally stops. Looking at an animation of both, one can tell that the linear interpolation looks strange,
and that makes sense because realistically it is impossible for anything to instantaneously change
velocity. The sinusoidal interpolation looks much more natural since it accelerates and decelerates
gradually, much like most things (including robotic arms) do in real life.
Click here to see my demo of sinusoidal vs. linear
movement.
Back to Top
Controls


