% HPP, FHP, and FHCP Implementation
% Abdulmajed Dakkak
% June 28th, 2008

Computational Fluid Dynamics with CA
====================================

Visualization
-------------

In virtually  all the  papers read,  the lattice  grid is  viewed as  a vector
field. This is done for several reasons:

* It's easy to visualize on paper whether the algorithm is working.
* It's the simplest to implement.

In NKS, for  example, Wolfram uses a  $96 \times 96$ subgrid  to approximate a
vector direction  on a 6 million  lattice grid. Previously in  his 1987 paper,
Wolfram used .... for a 4600(?) lattice grid.

HPP Model
=========

We represent each  lattice with $4$ vectors, each containing  is stored in its
own matrix. This means that `a[i][j]` contains the `a` vector component of the
lattice on the  $i^{th}$ row and $j^{th}$ column. With  this representation in
place, we perform the following to compute the next frame.

* Resolve  collisions  ---  the  collisions  are performed  and  stored  in  a
  temporary collision matrix.
* Propagation --- the propagation is performed  and values are copied from the
  temporary collision matrix into the `a`, `b`, `c`, and `d` matrices.

 <center>
 <img src="graphics/hpp-rep.png" width="200px">
 </center>

 \includegraphics[scale=0.1]{graphics/hpp-rep.png}

Collision
---------

Four temporary  matrices are created and  are called `K_a`, `K_b`,  `K_c`, and
`K_d` to signify which direction they correspond to. The vector `K_a[i][j]` is
the updated based on the HPP collision rules.

One can  represent the collision rules  as a series of  binary statements. The
best example is found in [^1]  where the authors represent the collision rules
as a binary statement.  Examples of the same binary statement  can be found in
other papers, however (**need to record them**)

$$a = a \otimes [(a \wedge c \wedge \neg (b \vee d)) \vee (b \wedge d \wedge \neg
(a \vee c))]$$

Where the logic operator symbols are 

* $\neg$ is the _not_ operator
* $\otimes$ is the _xor_ operator
* $\vee$ is the _or_ operator
* $\wedge$ is the _and_ operator

In `C`, the following code implements the above rule:

    for (x = 0; x < LATTICE_WIDTH; x++) {
        for (y = 0; y < LATTICE_HEIGHT; y++) {
            change = (a[x][y] & c[x][y] & ~(b[x][y] | d[x][y])) |
                     (b[x][y] & d[x][y] & ~(a[x][y] | c[x][y]));

            K_a[x][y] = a[x][y] ^ change;
            K_b[x][y] = b[x][y] ^ change;
            K_c[x][y] = c[x][y] ^ change;
            K_d[x][y] = d[x][y] ^ change;
        }
    }

The boolean expression allows us to perform the computation needed without the
use of  `if-else` statements. It  should be also noted  that we will  never go
outside the bounds of the array, the same cannot be said about the propagation
step. Also note that the expression 

    (a1[x][y] & c1[x][y] & ~(b1[x][y] | d1[x][y])) | 
    (b1[x][y] & d1[x][y] & ~(a1[x][y] | c1[x][y]))

Is repeated four times in the binary  representation, which is why we store it
in a separate value to reduce three computations.

Propagation
-----------

The HPP propagation step is the process of moving velocity vectors in the same
direction they are moving in after the collisions are resolved. Because of the
way we  oriented our grid, we  made this step unnecessarily  complicated. Also
it's not clear if our representation  has any advantages over a regular square
grid. Future  implementation (if  one is  needed) would  use a  regular square
grid.

 <center>
 <img src="graphics/hpp-grid.png" width="400px">
 </center>

 \includegraphics[scale=0.2]{graphics/hpp-grid.png}

We use the following code to propagation the vectors in the lattice

    a[i][j] = K_a[i-1][j-1];
    b[i][j] = K_b[i-1][j+1];
    c[i][j] = K_c[i+1][j+1];
    d[i][j] = K_d[i+1][j-1];

it should be evident that we will run  out of bounds if we run the above piece
of code over the  width of the lattice array. Since we do  not want to enforce
any boundary conditions at this stage of  the process, we place our lattice on
a toroidal  surface. This can  be easily implement in  `C` by noting  that the
following way to access and store array elements creates the toroidal surface:

    t[(i+n + LATTICE_HEIGHT) % LATTICE_HEIGHT][(j+m + LATTICE_WIDTH) % LATTICE_WIDTH]

and will also always be in the bounds of the matrix representation.

Optimizations
-------------

Since C  has no differentiation  between a boolean value  and a short,  we can
overload  a short  variable to  contain  multiple vector  values. The  boolean
expression  does  not change,  but  as  you see  from  the  figure below,  the
propagation step has to.

 <center>
 <img src="graphics/propgrid.png" width="400px">
 </center>

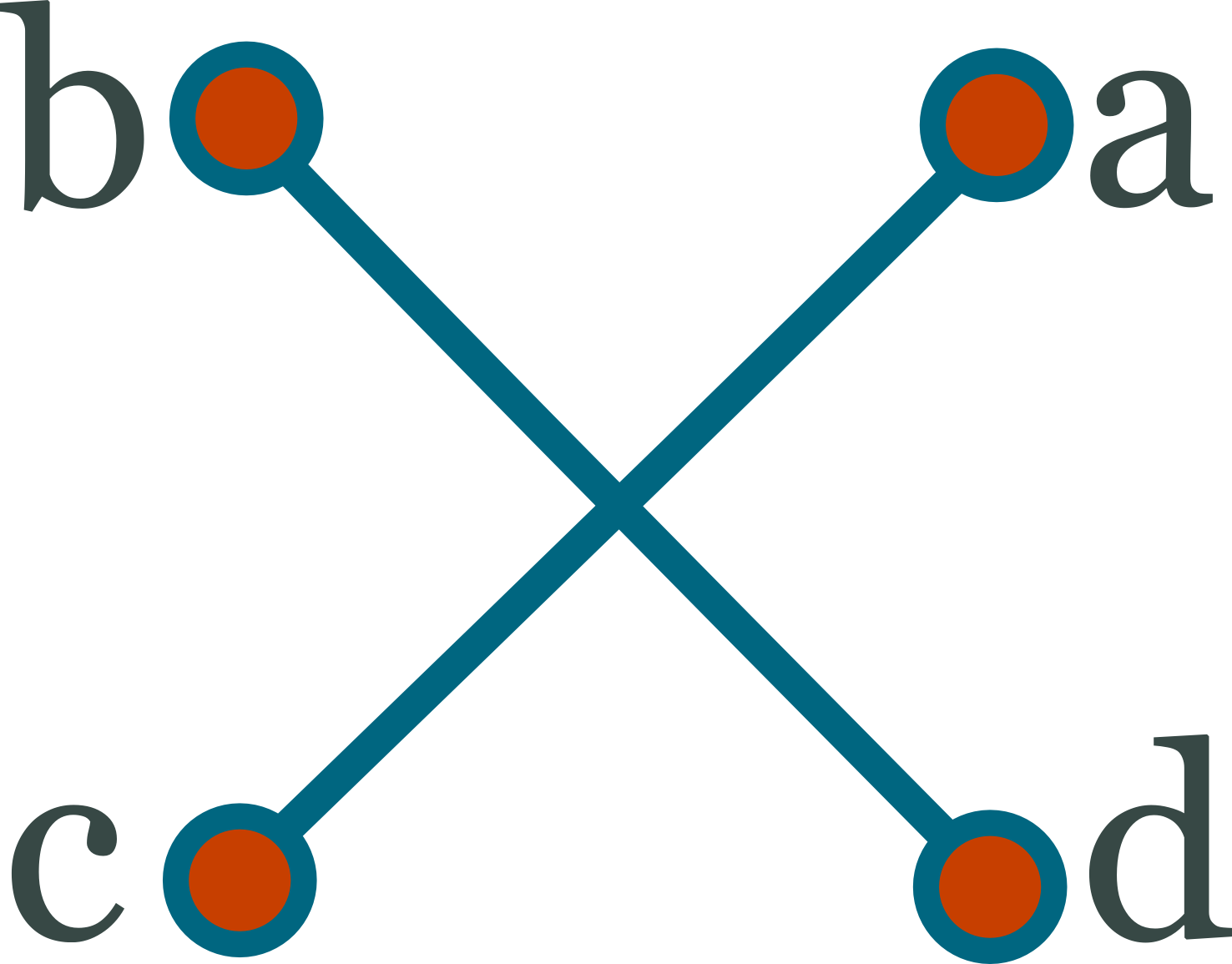 \includegraphics[scale=0.2]{graphics/propgrid.png}


The Code
--------

There are a  few differences between our implementation and  the one described
above:

1. The variables are  called `c1`, `c2`, `c3`, and `c4`  rather than `a`, `b`,
   `c`, and `d`.  The temporary collision arrays have also  been renamed to `k1`,
   `k2`, `k3`, and `k4`.
2. Our computation of blocks of vectors at a time forces us to use
   checkerboard propagation.

The crux of the code for HPP is provided bellow

    int x, y;
    short change;

    // Resolve Collisions
    for (x = 0; x < LATTICE_WIDTH; x++) {
        for (y = 0; y < LATTICE_HEIGHT; y++) {
            change = (a1[x][y] & c1[x][y] & ~(b1[x][y] | d1[x][y])) |
                     (b1[x][y] & d1[x][y] & ~(a1[x][y] | c1[x][y]));

            a2[x][y] = a1[x][y] ^ change;
            b2[x][y] = b1[x][y] ^ change;
            c2[x][y] = c1[x][y] ^ change;
            d2[x][y] = d1[x][y] ^ change;
        }
    }
    // Propagate
    for (x = 1; x < LATTICE_WIDTH - 1; x++) {
        for (y = 1; y < LATTICE_HEIGHT - 1; y += 2) {
            a1[x][y] = (a2[x][y - 1] >> 1) + (a2[x - 1][y - 1] << LAST);
            b1[x][y] = b2[x][y - 1];
            c1[x][y] = c2[x][y + 1];
            d1[x][y] = (d2[x][y + 1] >> 1) + (d2[x - 1][y + 1] << LAST);

            a1[x][y + 1] = a2[x][y];
            b1[x][y + 1] = (b2[x][y] << 1) + (b2[x + 1][y] >> LAST);
            c1[x][y + 1] = (c2[x][y + 2] << 1) + (c2[x + 1][y + 2] >> LAST);
            d1[x][y + 1] = d2[x - 1][y + 2];
        }
    }

CUDA
----

Never implemented.

FHP Model
=========

Collision
---------

Propagation
-----------

The Code
--------

Optimizations
-------------

CUDA
----

FCHC Model
==========

In the _Face Centered Hyper Cubic_ model, you have 24 vectors. 16 correspond
to the vertexes of the hyper cube while the other 8 correspond to the center
of the squares in the hyper cube.

Reduction
---------
Since you cannot store the entire table, you consider only states that have a
normalized momentum. The coordinates of the momentum $q$ are defined by

$$q_\alpha = \sum_{i = 0}^{24} S_i C_{i \alpha}$$

where $S_i$ is a boolean variable signifying the presence or absence of a
particle with velocity $C_i$. The momentum is normalized if the coordinates
satisfy

$$q_1 > q_2 > q_3 > q_4 > |q_1 - q_2 - q_3|$$

Different isometries are then applied if one of the following conditions are
satisfied in the following sequence:

* if $q_1 < 0$, then $S_1$ is applied to $q$
* if $q_2 < 0$, then $S_2$ is applied to $q$
* if $q_3 < 0$, then $S_3$ is applied to $q$
* if $q_4 < 0$, then $S_4$ is applied to $q$
* if $q_1 < q_2$, then $P_{12}$ is applied to $q$
* if $q_3 < q_4$, then $P_{34}$ is applied to $q$
* if $q_1 < q_3$, then $P_{13}$ is applied to $q$
* if $q_2 < q_4$, then $P_{24}$ is applied to $q$
* if $q_2 < q_3$, then $P_{23}$ is applied to $q$
* if $q_1 + q_4 < q_2 + q_4$, then $\Sigma_1$ is applied to $q$
* if $q_1 < q_2 + q_3 + q_4$, then $\Sigma_2$ is applied to $q$

Where

* $S_\alpha$ is the symmetry with respect to the plane $x_\alpha = 0$
* $P_{\alpha \beta}$ is the symmetry with respect to the plane 
    $x_\alpha = x_\beta$
* $\Sigma_1$ is the symmetry with respect to the plane
    $x_1 + x_4 = x_2 + x_3$
* $\Sigma_2$ is the symmetry with respect to the plane
    $x_1 = x_2 + x_3 + x_4$





[^1]: Wolf-Gladrow, Dieter. Lattice-Gas Cellular Automata and Lattice Boltzmann Models: an Introduction. Santa Clara: Springer-Verlag TELOS, 2000.
  ([pdf][wolf.book])

[wolf.book]: ../papers/files/Wol2000c.pdf