% What if DNA Lived on a Lattice?
% Abdulmajed Dakkak
% June 10th, 2008
> These are my notes based on the lecture by Dr. Zoie Raputi on June 10th,
> 2008. Please email me with corrections if mistakes are found.
In this talk the presenter simplifies the DNA model by assuming that they live
on a lattice. After defining legal local moves, the presenter is interested in
the speedup achieved if such moves are allowed to be executed in parallel.
The DNA
=======
DNA is the blueprint that instructs the cells how to replicate. It is composed
of a combination of phosphates and sugar, with bases that, for simplicity,
reside on top of the sugars. Such bases are called _monomers_ and come in four
types --- Adenine, Thymine, Guanine, and Cytosine. The two basis Adenine and
Thymine bond to create a _weak_ pair composed of two hydrogen bonds. The
_stronger_ pair is composed of 3 hydrogen bonds and is composed of Guanine and
Cytosine.
It is known from experiments that if the DNA is single stranded and a
periodic, then it can loop onto itself. If such loops occur, then they are
called either _hairpins_ or _stem-loop structures_. It is worth mentioning
that loops are not a strange phenomenon in DNA, as they only lasts for a few
milliseconds --- although some believe that continuous oscillation occurs. The
figure bellow shows a single stranded DNA in open (or coil) state on the left,
and a strand of DNA in closed (or native) state on the right. These correspond
to the kinetics of the DNA strand.
 \includegraphics[scale=0.15]{graphics/hairpins.png}
The Lattice
===========
The presenter simplifies the DNA onto a lattice considering both a cubical and
hexagonal lattice in 2 and 3 space. She then defines what local moves and
configurations are legal, and which are not. Such moves are influenced by how
DNA behaves at the microscopic level. One constraint is the so called
_stiffness constrain_. It states that the angle between two consecutive bond
(edges in the lattice) must be larger than $120^\circ$.
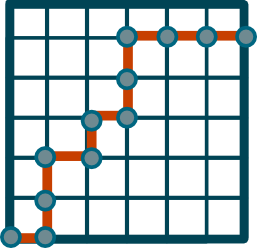
Square Lattice
--------------
The square lattice is the simplest lattice to discritize the DNA on. There are
only two directions $x_1$ and $x_2$ (the inverse directions $x^{-1} = x_1$
and $y^{-1} = y_1$ being trivial due to the symmetry of the square). Since
no restriction is placed on the configuration, all words are considered legal.
\includegraphics[scale=0.15]{graphics/hairpins.png}
The Lattice
===========
The presenter simplifies the DNA onto a lattice considering both a cubical and
hexagonal lattice in 2 and 3 space. She then defines what local moves and
configurations are legal, and which are not. Such moves are influenced by how
DNA behaves at the microscopic level. One constraint is the so called
_stiffness constrain_. It states that the angle between two consecutive bond
(edges in the lattice) must be larger than $120^\circ$.
Square Lattice
--------------
The square lattice is the simplest lattice to discritize the DNA on. There are
only two directions $x_1$ and $x_2$ (the inverse directions $x^{-1} = x_1$
and $y^{-1} = y_1$ being trivial due to the symmetry of the square). Since
no restriction is placed on the configuration, all words are considered legal.
 \includegraphics[scale=0.3]{graphics/square.png}
Cubic Lattice
-------------
The cubical lattice contains three directions $x, y,$ and $z$. The inverses
are again trivial to deduce, and, since no restriction is placed on the
placement of the DNA, all words are legal.
\includegraphics[scale=0.3]{graphics/square.png}
Cubic Lattice
-------------
The cubical lattice contains three directions $x, y,$ and $z$. The inverses
are again trivial to deduce, and, since no restriction is placed on the
placement of the DNA, all words are legal.
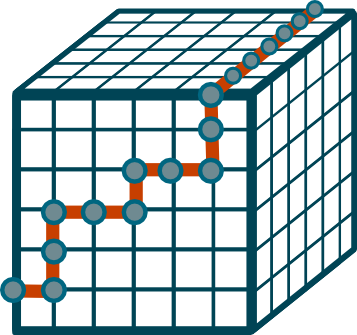 \includegraphics[scale=0.3]{graphics/cube.png}
If we consider the 2-dimensional cubic lattice where the directions $x, y,$
and $z$ form $0^\circ, 60^\circ$, or $120^\circ$. In this case some words are
not allowed since they conflict with our stiffness constraint. One can
enumerate all the legal words in this lattice and get:
xy yx
yz zy
It is easy to see how one can get this if we represent $x$, $y$ and $z$ as
vectors in $\mathbb{R}^2$.
$x = \langle 1, 0 \rangle$,
$y = \langle \frac{1}{2}, \frac{\sqrt{3}}{2} \rangle$, and
$z = \langle \frac{-1}{2}, \frac{\sqrt{3}}{2} \rangle$
If we consider the 3-dimensional cubical lattice, there are are a total of 6
directions $x_i$ for $i = 0, 1, \cdots, 6$. The first three are planer and are
the same as the 2-dimensional cubical lattice case. The other three spring out
of two dimensions and are
$\langle \frac{-1}{2}, \frac{-1}{2\sqrt{3}}, \frac{\sqrt{2}}{\sqrt{3}} \rangle$,
$\langle \frac{1}{2}, \frac{-1}{2\sqrt{3}}, \frac{\sqrt{2}}{\sqrt{3}} \rangle$, and
$\langle 0, \frac{1}{\sqrt{3}}, \frac{\sqrt{2}}{\sqrt{3}} \rangle$
.
Allowable Moves
===============
\includegraphics[scale=0.3]{graphics/cube.png}
If we consider the 2-dimensional cubic lattice where the directions $x, y,$
and $z$ form $0^\circ, 60^\circ$, or $120^\circ$. In this case some words are
not allowed since they conflict with our stiffness constraint. One can
enumerate all the legal words in this lattice and get:
xy yx
yz zy
It is easy to see how one can get this if we represent $x$, $y$ and $z$ as
vectors in $\mathbb{R}^2$.
$x = \langle 1, 0 \rangle$,
$y = \langle \frac{1}{2}, \frac{\sqrt{3}}{2} \rangle$, and
$z = \langle \frac{-1}{2}, \frac{\sqrt{3}}{2} \rangle$
If we consider the 3-dimensional cubical lattice, there are are a total of 6
directions $x_i$ for $i = 0, 1, \cdots, 6$. The first three are planer and are
the same as the 2-dimensional cubical lattice case. The other three spring out
of two dimensions and are
$\langle \frac{-1}{2}, \frac{-1}{2\sqrt{3}}, \frac{\sqrt{2}}{\sqrt{3}} \rangle$,
$\langle \frac{1}{2}, \frac{-1}{2\sqrt{3}}, \frac{\sqrt{2}}{\sqrt{3}} \rangle$, and
$\langle 0, \frac{1}{\sqrt{3}}, \frac{\sqrt{2}}{\sqrt{3}} \rangle$
.
Allowable Moves
===============



